L10 // Обобщенные линейные модели. Логистическая регрессия. Пуассоновская регрессия

Антон Ангельгардт

Что будет?

• логика обобщенных линейных моделей
• моделирование бинарных переменных
• моделирование счетных переменных

L10.1 // Логистическая регрессия

Ограничения общих линейных моделей

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p + \varepsilon \]

\[ \varepsilon \thicksim N (0, \sigma^2) \]

\[ y \thicksim N (\mu, \sigma^2) \]

Идея обобщенных линейных моделей

• функция связи (link function)

• \(y \thicksim f(y|\theta)\), \(\theta\) — параметр(ы) распределения

• хотим моделировать \(\mathbb{E}(y)\)

• преобразование (функция) \(g \big( \mathbb{E}(y) \big) = \eta\), линеаризующее матожидание — функция связи

• линейная величина \(\eta\)

\[ \eta_i = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p + \varepsilon \]

• изучаем не \(\eta\), а \(\mathbb{E}(y)\) — обратная функцию \(g^{-1} (\eta) = \mathbb{E}(y)\)

Обобщенные линейные модели (generalized linear models, GLM)

\[ g \big( \mathbb{E}(y_i) \big) = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} + \varepsilon_i \]

Функция идентичности

• \(g \big( \mathbb{E}(y)) = \mu\), \(y \thicksim N (\mu, \sigma^2)\)

\[ g \big( \mathbb{E}(y_i) \big) = \mu_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} + \varepsilon_i \]

Бинарные переменные

• \(0\) и \(1\)

\[ \mathbb{P}(X = k) = C_n^k \, p^k \, q^{n-k} \]

Биномиальное распределение

\(\mathbb{P}(X = k) \thicksim \text{Bin}(n, p)\)

Математическая модель

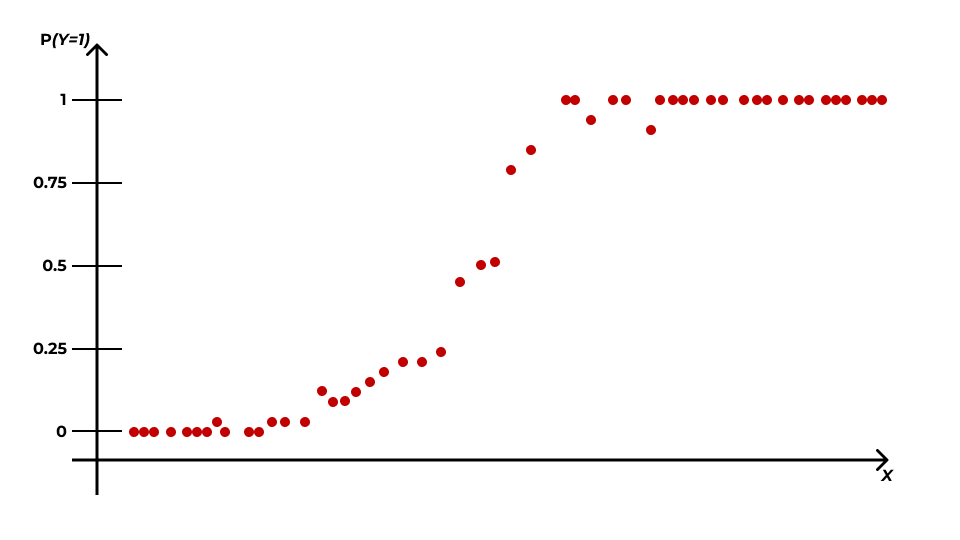
Математическая модель

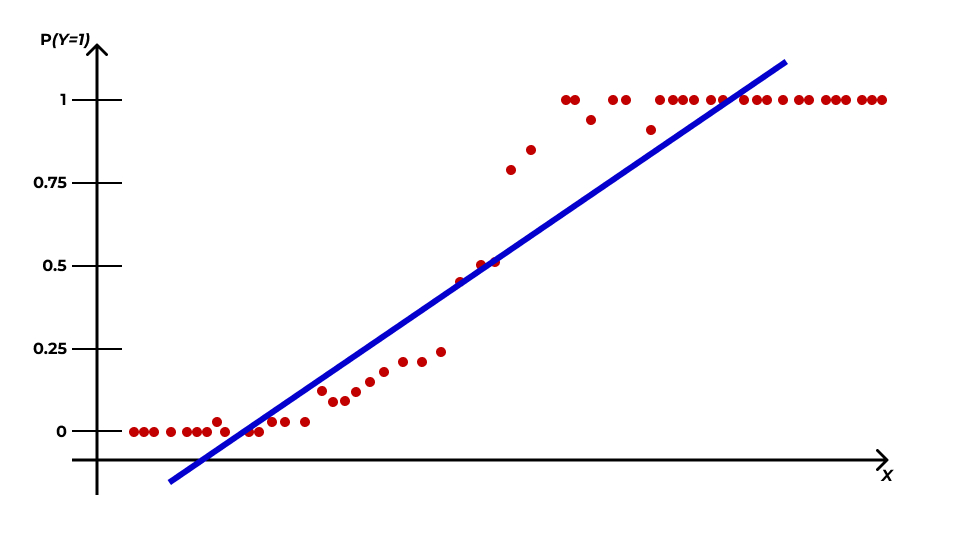
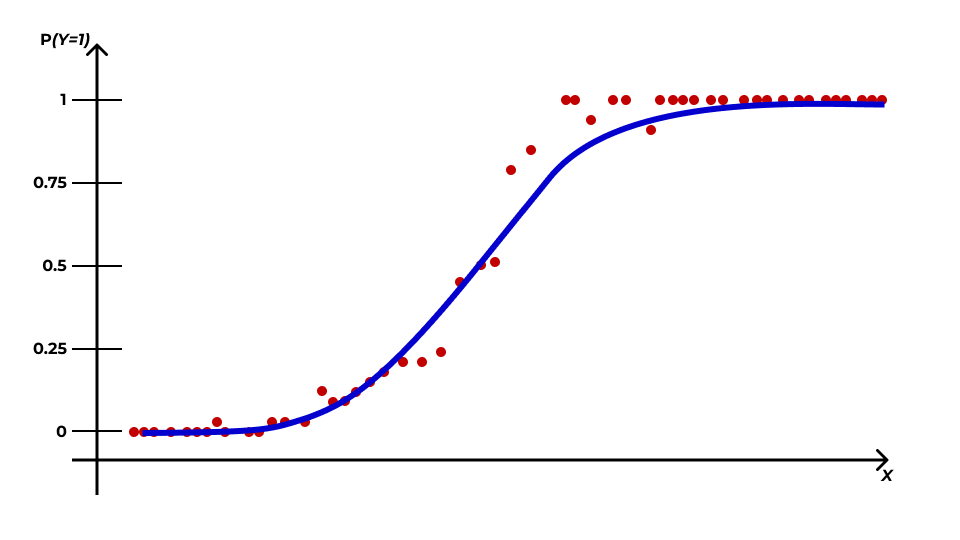
Логистическая кривая

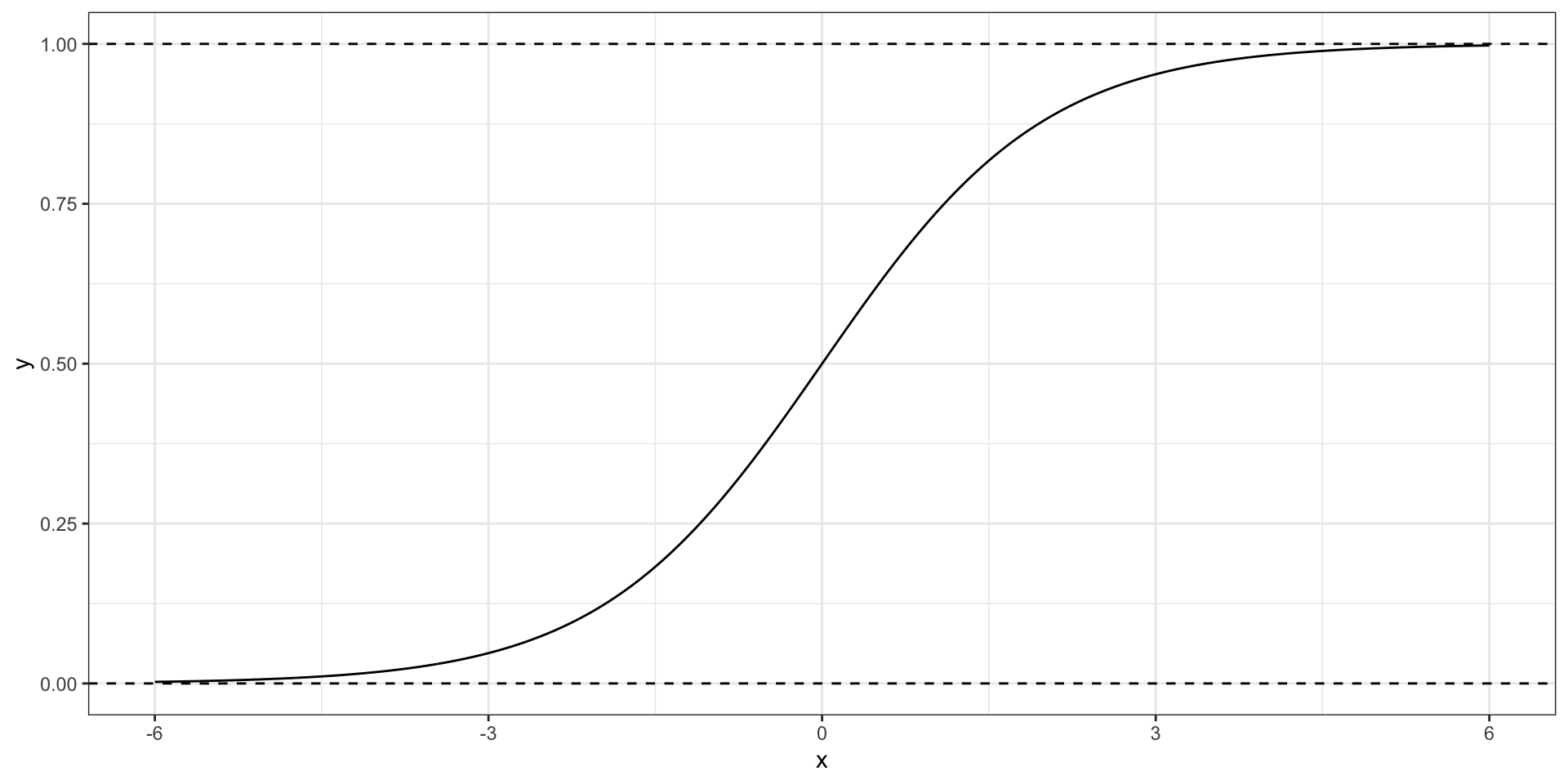
\[ y = \frac{e^x}{1 + e^x} \]

Уравнение логистической регрессии

\[ \mathbb{P}(Y=1|x_i) = p_i = \frac{e^{ \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots \beta_p x_{ip}} } {1 + e^{ \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots \beta_p x_{ip}} } \]

Шансы и логиты

Шанс (отношение шансов, odds, odds ratio) — это отношение вероятности «успеха» (\(1\)) к вероятности «неудачи» (\(0\))

• от \(0\) до \(+\infty\).

\[ \text{odds}_i = \frac{\mathbb{P}(Y=1|x_i)}{1 - \mathbb{P}(Y=1|x_i)} = \frac{p_i}{1 - p_i} \]

Logit-преобразование

\[ \text{logit}(p_i) = \ln \left(\frac{p_i}{1 - p_i} \right) \]

• от \(-\infty\) до \(+\infty\)
• симметричны относительно нуля
• линейны

Линеаризация логистической кривой через logit-преобразование

\[ p_i = \frac{e^{\beta_0 + \beta_1 x_{i1}}} {1 + e^{\beta_0 + \beta_1 x_{i1}}} \]

\[ \beta_0 + \beta_1 x_{i1} = t_i \]

\[ \text{logit} (p_i) = \ln \left(\frac{p_i}{1 - p_i} \right) \]

\[ \ln \left(\frac{p_i}{1 - p_i} \right)\overset{\text ?}{=} t_i \]

\[ \begin{split} \ln \left(\frac{p}{1-p} \right)&= \\ &= \ln \left(\frac{\frac{e^t}{1 + e^t}}{1 - \frac{e^t}{1 + e^t}} \right)= \\ &= \ln \left(\frac{e^t}{1 + e^t} \right)- \ln \left(1 - \frac{e^t}{1 + e^t} \right)= \\ &= \ln \left(\frac{e^t}{1 + e^t} \right)- \ln \left(\frac{1 + e^t - e^t}{1 + e^t} \right)= \\ &= \ln \left(\frac{e^t}{1 + e^t} \right)- \ln \left(\frac{1}{1 + e^t} \right)= \\ &= \ln (e^t) - \ln (1 + e^t) - \big(\ln (1) - \ln (1+e^t)\big) = \\ &= \ln (e^t) - \ln (1) = \\ &= \ln (e^t) = t \end{split} \]

Cаммари того, что происходило выше

• От дискретной оценки событий (0 и 1) переходим к оценке вероятностей.
• Связь вероятностей с предиктором описывается логистической кривой.
• Если при помощи функции связи перейти от вероятностей к логитам, то связь будет описываться прямой линией.
• Параметры линейной модели для такой прямой можно оценить с помощью регрессионного анализа.

Математическая модель логистической регрессии

\[ p_i = \frac{e^{\beta_0 + \beta_1 x_{i1}}} {1 + e^{\beta_0 + \beta_1 x_{i1}}} \]

\[ \text{logit} (p_i) = \ln \left(\frac{p_i}{1 - p_i} \right)= \eta_i \]

\[ \eta_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} \]

\[ p_i = \frac{e^{\eta_i}}{1 + e^{\eta_i}} \]

Идентификация модели

• задача индентификации модели логистической регрессии не имеет аналитического решения
• используются численные методы для получения оценок коэффициентов

Метод максимального правдоподобия

Правдоподобие (likelihood) — это способ измерить соответствие имеющихся данных тому, что можно получить при определенных значениях параметров модели.

\[ L(\theta|\text{data}) = \prod_{i=1}^n f(\text{data}|\theta), \]

где \(f(\text{data}|\theta)\) — функция распределения с параметрами \(\theta\).

Задача идентификации модели решается максимизацией функции правдоподобия по параметрам модели

\[ L(\theta|\text{data}) \to \max_{\mathbf{b}} \]

\[ \ln \big( L(\theta | \text{data}) \big) \to \max_{\mathbf{b}} \]

Девианса (deviance)

• Насыщенная модель (saturated model) — модель, в которой каждое наблюдение (сочетание предикторов) описывается одним из \(n\) параметров.

\[ \begin{split} & \ln L_\text{sat} = 0 \\ & \text{df}_\text{sat} = n - p_\text{sat} = n - n = 0 \end{split} \]

• Нулевая модель (null model) — модель, в которой все наблюдения описываются одним параметром (средним значением).

\[ \begin{split} & \eta_i = \beta_0 \\ & \ln L_\text{null} \neq 0, \; \ln L_\text{null} \to -\infty \\ & \text{df}_\text{null} = n - p_\text{null} = n - 1 \end{split} \]

• [Предложенная] модель находится где-то между насыщенной и нулевой моделями

\[ \begin{split} & \eta_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} \\ & \ln L_\text{model} \neq 0 \\ & \text{df}_\text{model} = n - p_\text{model} \end{split} \]

Девианса (deviance)

Девианса является мерой различия правдоподобий двух моделей (оценка разницы логарифмов правдоподобий)

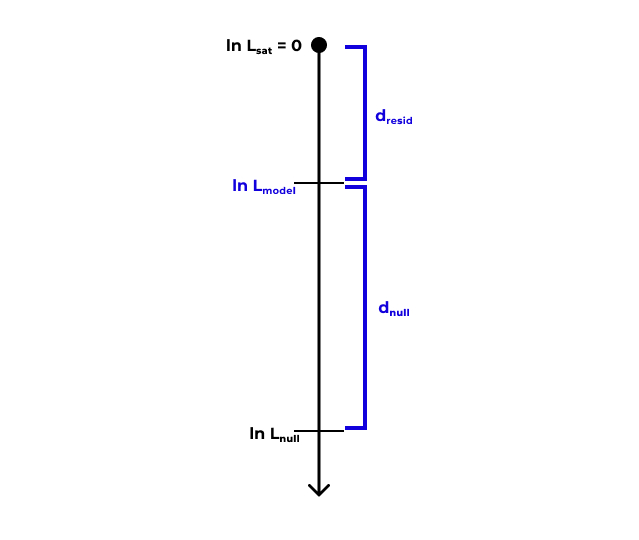
• Остаточная девианса: \(d_\text{resid} = 2(\ln L_\text{sat} - \ln L_\text{model}) = -2 \ln L_\text{model}\)
• Нулевая девианса: \(d_\text{null} = 2(\ln L_\text{sat} - \ln L_\text{null}) = -2 \ln L_\text{null}\)

Анализ девиансы

• тест отношения правдоподобий (likelihood ratio test, LRT)

\[ \begin{split} d_\text{null} - d_\text{resid} &= \\ &= -2 (\ln L_\text{null} - \ln L_\text{model}) = \\ &= 2 (\ln L_\text{model} - \ln L_\text{null}) = \\ &= 2 \ln \left(\frac{L_\text{model}}{L_\text{null}} \right) \end{split} \]

\[ \text{LRT} = 2 \ln \left(\frac{L_\text{M1}}{L_\text{M2}} \right)= 2 (\ln L_\text{M1} - \ln L_\text{M2}), \]

• \(\text{M1}\) и \(\text{M2}\) — вложенные модели
  • \(\text{M1}\) — более полная
  • \(\text{M2}\) — сокращенная

Распределение разницы логарифмов правдоподобий аппроксимируется распределением \(\chi^2\) со степенями свободы \(\text{df} = \text{df}_\text{M2} - \text{df}_\text{M1}\).

Тестирование значимости модели

\[ \begin{split} & \text{LRT} = 2 \ln \left(\frac{L_\text{model}}{L_\text{null}} \right)= 2 (\ln L_\text{model} - \ln L_\text{null}) = d_\text{null} - d_\text{model} \\ & \text{df} = p_\text{model} - 1 \end{split} \]

Тестирование значимости предикторов

\[ \begin{split} & \text{LRT} = 2 \ln \left(\frac{L_\text{model}}{L_\text{reduced}} \right)= 2 (\ln L_\text{model} - \ln L_\text{reduced}) \\ & \text{df} = p_\text{model} - p_\text{reduced} \end{split} \]

Псевдо-\(R^2\)

• доля объясненной девиансы

\[ \frac{d_\text{null} - d_\text{residual}}{d_\text{null}} \]

Информационные критерии

• баейсовский (Bayesian information criterion, BIC)
• информационный критерий Акаике (Akaike information criterion, AIC)
• чем ниже значение информационного критерия, тем лучше модель описывает имеющиеся данные

Допущения логистической регрессии

• независимость наблюдений
• линейность связи целевой переменной и предикторов (с учетом функции связи)
• отсутствие коллинеарности предикторов
• отсутствие сверхдисперсии

Проверка на сверхдисперсию

\[ \begin{split} & \mathbb{E}(X) = np \\ & \text{var}(X) = np(p-1) \end{split} \]

• \(n\) — количество испытаний
• \(p\) — вероятность «успеха» в одном испытании

Если обнаруживается свердисперсия, то мы не можем гарантировать, что закономерность смоделирована точно.

Тесты Вальда

• аналогом t-тестов для общих линейных моделей
• являются менее точными, так как распределение их z-статистики только ассимптотически стремится к нормальному
• на малых выборках эти тесты буду давать неточные результаты

\[ \begin{split} H_0 &: \beta_k = 0 \\ H_1 &: \beta_k \neq 0 \end{split} \]

\[ z = \frac{b_k - \beta_k}{\text{se}_{b_k}} = \frac{b_k}{\text{se}_{b_k}} \thicksim N(0, 1) \]

Интерпретация коэффициентов модели

\[ \eta_i = \hat \beta_0 + \hat \beta_1 x_{i1} + \hat \beta_2 x_{i2} + \dots + \hat \beta_p x_{ip} \]

• \(\hat \beta_0\), интерсепт, показывает логарифм отношения шансов для случая, когда значения всех предикторов равны нулю
• \(\hat \beta_k\) показывает, на сколько изменится логарифм отношения шансов при изменении значения предиктора на единицу

Суть коэффициентов через математику

\[ \eta = b_0 + b_1 x \]

\[ \eta = \ln \left(\frac{p}{1-p} \right)= \ln (\text{odds}) \]

\[ \eta_{x+1} - \eta_x = \ln (\text{odds}_{x+1}) - \ln (\text{odds}_x) = \ln \left(\frac{\text{odds}_{x+1}}{\text{odds}_x} \right) \]

\[ \begin{split} \eta_{x+1} - \eta_x &= \big( b_0 + b_1(x+1) \big) - \big( b_0 + b_1 x \big) = \\ &= b_0 + b_1 x + b_1 - b_0 - b_1 x = b_1 \end{split} \]

\[ \begin{split} \ln \left(\frac{\text{odds}_{x+1}}{\text{odds}_x} \right)&= b_1 \\ \frac{\text{odds}_{x+1}}{\text{odds}_x} = e^{b_1} \end{split} \]

Интерпретация коэффициентов

• \(e^{b_1}\) показывает, во сколько раз изменится шанс того, что наблюдение принадлежит к группе «единиц» при увеличении предиктора на единицу
• для дискретных предикторов — во сколько раз различается отношение шансов для данного уровня предиктора по сравнению с базовым

Предсказательная сила модели

• в данных — нули и единицы
• модель возвращает вероятность единицы
• необходимо перевести непрерывные предсказания в дискретные
• выбрать порог
  • если значение вероятности выше него — модель предсказала \(1\),
  • если ниже — то \(0\).

Значение порога влияет на качество модели.

Confusion mattrix

	Предсказания: \(0\)	Предсказания: \(1\)
Данные: \(0\)	\(\text{TN}\)	\(\text{FP}\)
Данные: \(1\)	\(\text{FN}\)	\(\text{TP}\)

• True Positive (\(\text{TP}\)) — верное предсказанные единицы
• True Negative (\(\text{TN}\)) — верно предсказанные нули
• False Positive (\(\text{FP}\)) — ложноположительные предсказания, ошибочно предсказанные единицы
• False Negative ($ — ложноотрицательные предсказания, ошибочно предсказанные нули

Accuracy

\[ \text{accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}} \]

• хорошо работает на сбалансированных данных
• на несбалансированных данных может скажать реальность

Несостоятельность accuracy

• Данные:

\[ \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 \end{pmatrix} \]

• Модель всегда предсказывает ноль
• Accuracy — \(0.73\)

Precision

• доля верно предсказанных единиц

\[ \text{precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} \]

Recall

• долю предсказанных единиц из всех единиц датасета

\[ \text{recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} \]

F1-мера

\[ \text{F1} = 2 \cdot \frac{\text{precision} \cdot \text{recall}}{\text{precision} + \text{recall}} \]

ROC-AUC

№ наблюдения	Вероятность
1	1.00
2	0.90
3	0.80
4	0.75
5	0.60
6	0.50
7	0.43
8	0.32
9	0.20
10	0.15

№ наблюдения	Вероятность	Значение
1	1.00	1
2	0.90	1
3	0.80	0
4	0.75	1
5	0.60	0
6	0.50	1
7	0.43	0
8	0.32	0
9	0.20	0
10	0.15	0

ROC-AUC

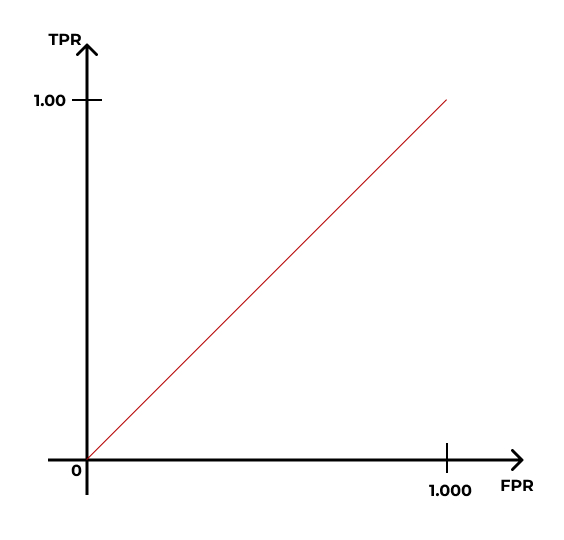
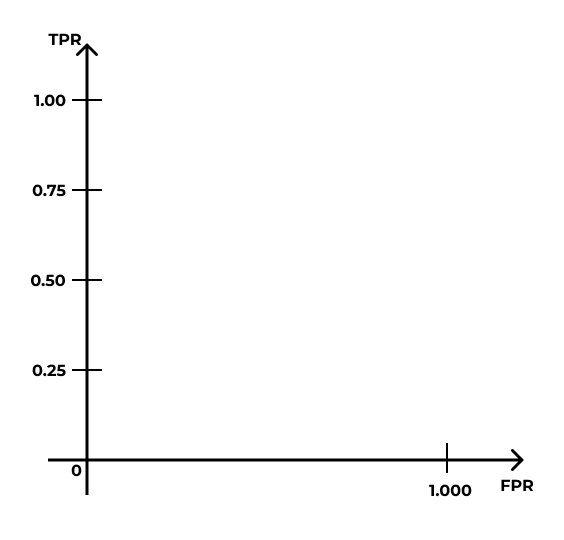
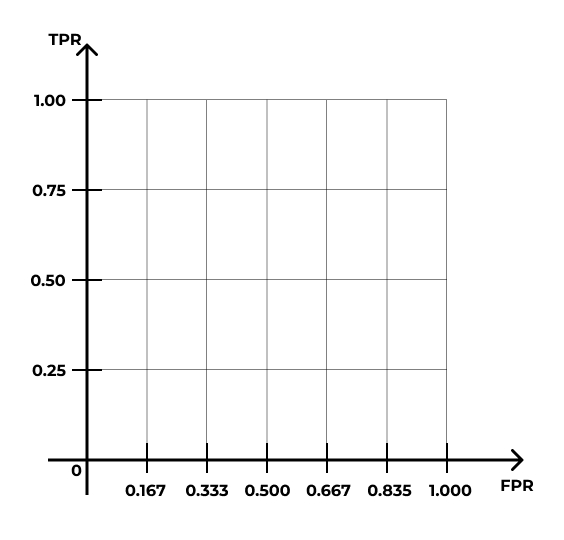
ROC-AUC

• ROC-кривая (receiver operating characteristic)

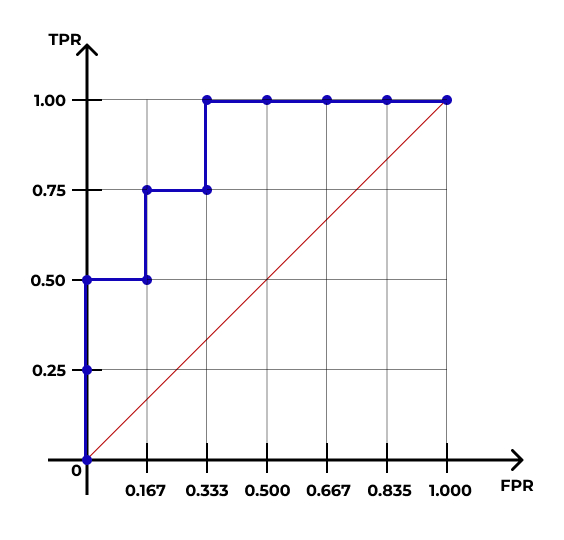
• AUC — area under curve

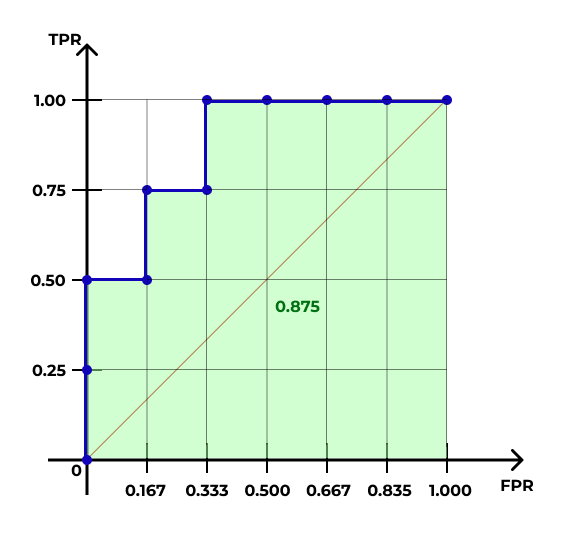
L10.2 // Пуассоновская регрессия

Счетные данные

• число комнат в квартире
• количество детей в семье
• число книг на полке
• число людей, прошедших через турникет

Свойства счетных величин

• Они могут принимать только неотрицательные целочисленные значения (\(x_i \in \mathbb{N}_{0}\))
• Разброс значений зависит от среднего значения (\(\text{var}(X) \propto \mathbb{E}(X)\))

Распределение Пуассона

\[ Y \thicksim \text{Poisson} (\mu) \]

\[ f(y) = \frac{\mu^y e - \mu}{y!} \]

\[ \begin{split} \mathbb{E}(Y) = \mu \\ \text{var}(Y) = \mu \end{split} \]

Форма распределения Пуассона

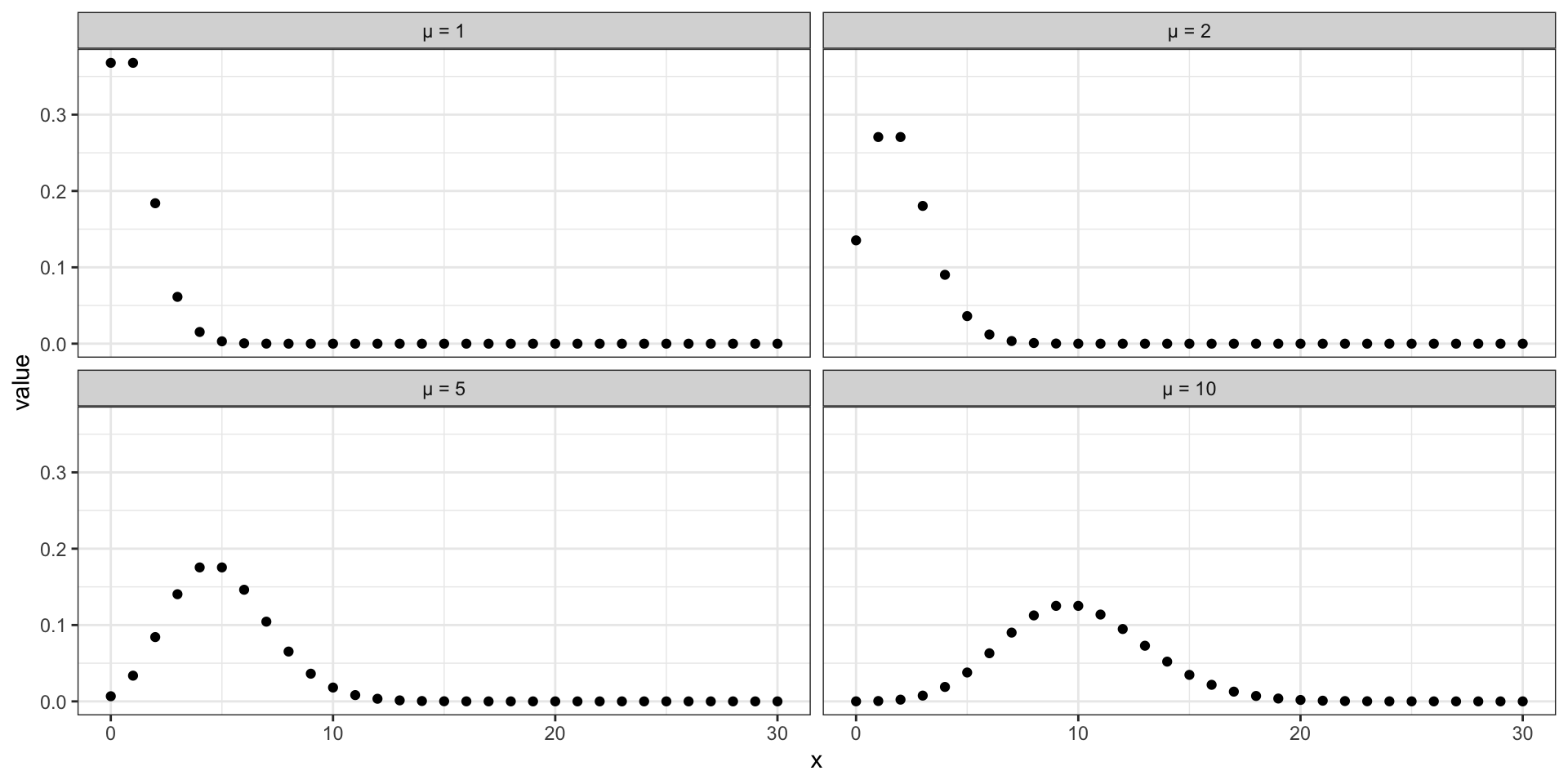
Почему общие линейные модели плохо работают?

• линейнная регрессия будет предсказывать отрицательные значения

• изначально не выполнено допущение гомоскедастичности остатков

• оценки коэффициентов модели будут неточны

• ошибки завышены

• результатам статистического тестирования доверять нельзя

Математическая модель

\[ \eta_i = \ln (y_i) \]

\[ \eta_i = \hat \beta_0 + \hat \beta_1 x_{i1} + \hat \beta_2 x_{i2} + \dots + \hat \beta_p x_{ip} \]

Результаты моделирования

• отсутствует \(F\)-статистика
• отсутствует \(R^2\)
• необходим анализ девиансы
• z-тесты Вальда
• проверка на сверхдисперсию

Роль сверхдисперсии

• пуассоновская модель предполагает равенство дисперсии и математического ожидания
• если нет, то
  • оценки стандартных ошибок коэффициентов будут занижены
  • тесты Вальда для коэффициентов модели дадут неправильные результаты — из-за того, что оценки стандартных ошибок занижены— уровень значимости будет занижен
  • тесты, основанные на сравнении правдоподобий, дадут смещенные результаты, так как соотношение девианс уже не будет подчиняться распределению \(\chi^2\)

Почему?

• Для пуассоновского распределения:

\[ \begin{split} & \text{var}(y_i) = \mu_i \\ & \text{var}(\mathbb{E}(y_i)) = \frac{\mu}{n} \\ & \text{se}_{\mathbb{E}(y_i)} = \sqrt{\text{var}\big( \mathbb{E}(y_i) \big)} \end{split} \]

• Если сверхдисперсия, то дисперсия в \(\phi\) раз больше среднего (\(\phi > 1\)):

\[ \begin{split} & \text{var}(y_i) = \phi \mu_i \\ & \text{var}(\mathbb{E}(y_i)) = \frac{\phi \mu}{n} \\ & \text{se}_{\mathbb{E}(y_i)} = \sqrt{\phi \text{var}\big( \mathbb{E}(y_i) \big)} \end{split} \]

Квазипуассоновские модели

• основываются на распределение Пуассона
• учитывают коэффициет \(\phi\) —- поправка на сверхдисперсию
• модель не меняется
• коэффициент \(\phi\) оценивается по данным
• оценки параметров пуассоновских и квазипуассоновских моделей совпадают
• стандартные ошибки коэффициентов домножатся на \(\sqrt{\phi}\)
• доверительные интервалы коэффициентов домножаются на \(\sqrt{\phi}\)
• логарифмы правдоподобий, используемые для тестирования статистической значимости моделей, уменьшаются в \(\phi\) раз
• для анализа девиансы используются F-тесты
• для тестирования эначимости коэффициентов используются t-тесты

Итоги

• фреймворк обобщенных линейных моделей
• модель логистической регрессии
• девианса и её возможности
• confusion matrix и предсказательная сила
• счетные данные и пуассоновские модели
• сверхдисперсия и кувазипуассоновские модели

L10 // Обобщенные линейные модели. Логистическая регрессия. Пуассоновская регрессия

Антон Ангельгардт