L11 // Регуляризация регрессии. Обобщенные аддитивные модели
Зачем?
- Развитие идеи обобщенных линейных моделей
- Моделирование нелинейных закономерностей
- Особенности и подводные камни
- Снова мультиколинеарность
- Штраф за большие ошибки
- Преимущества и недостатки
L11.1 // Обобщенные аддитивные модели
Recap
- LM
\[ y = b_0 + b_1 x_1 + b_2 x_2 + \dots + b_p x_p + e \]
- GLM
\[ g(y) = b_0 + b_1 x_1 + b_2 x_2 + \dots + b_p x_p + e \]
Но есть закономерность нелинейная? Прям вот ваще нелинейная?
Нелинейные закономерности
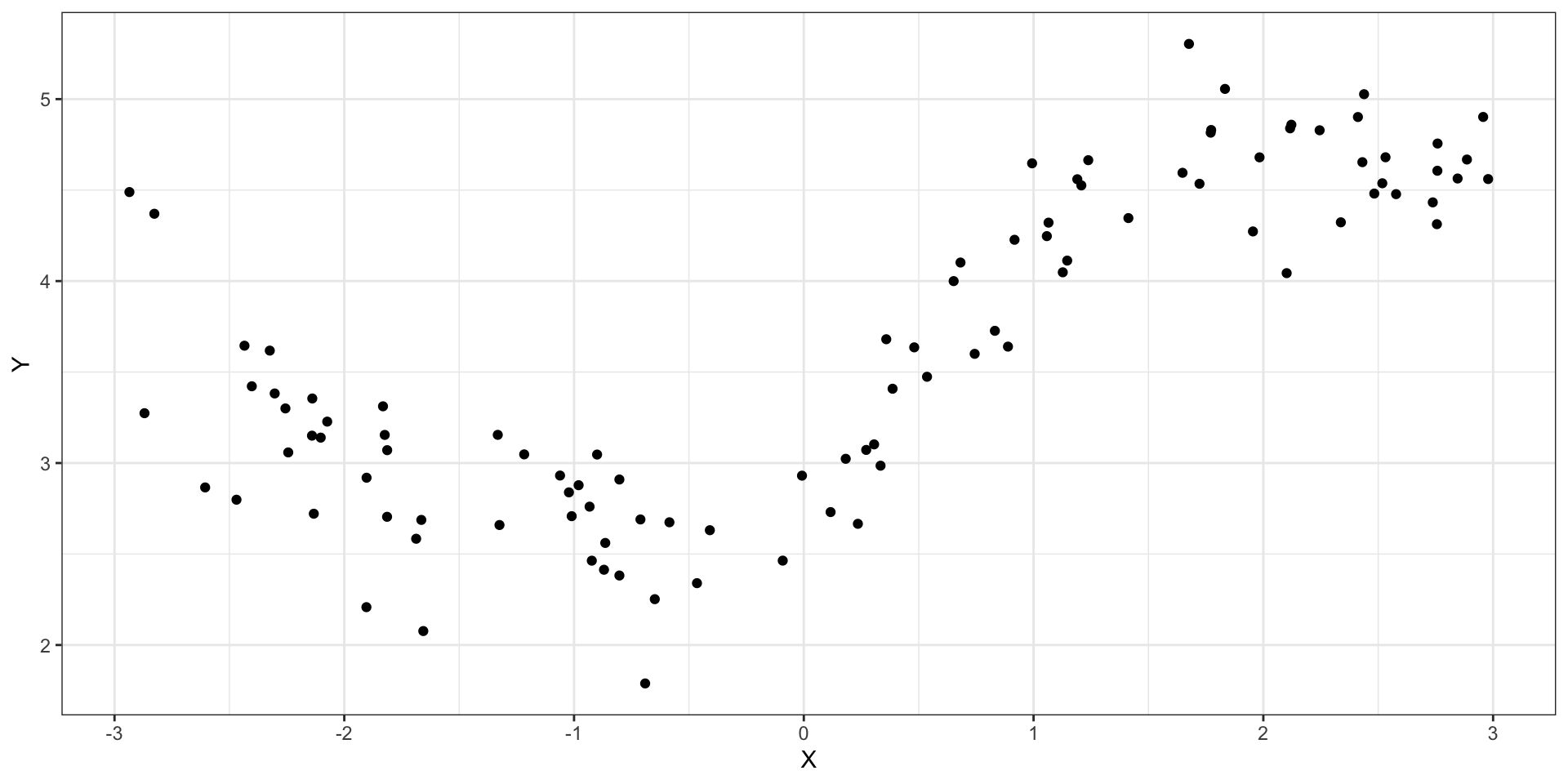
Изученные модели плохо работают
- общая линейная модель
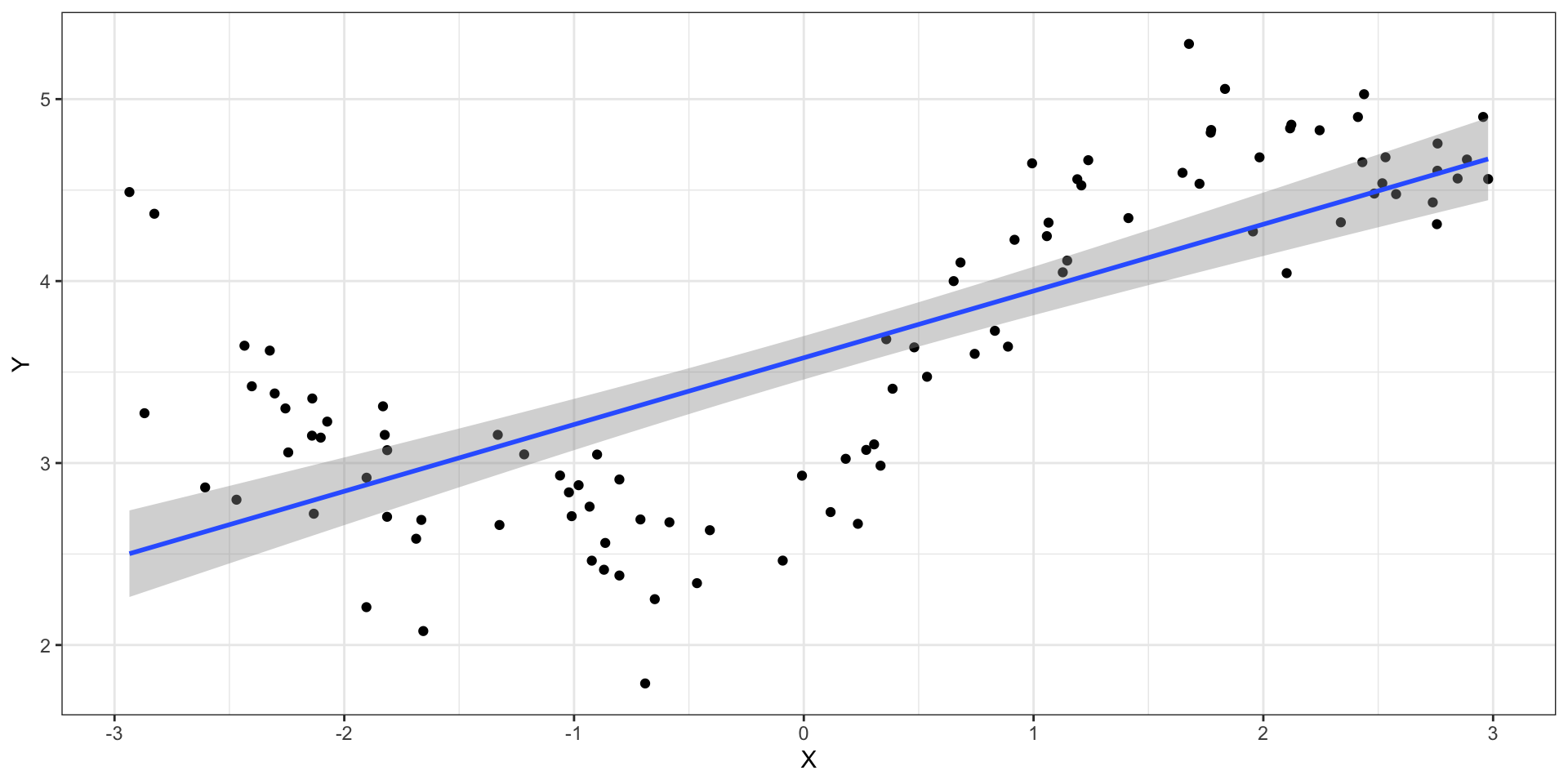
- \(Y\) — количественная переменная, для GLM сложно придумать функцию связи, которая сможет линеаризовать закономерность
Полиномиальная регрессия
полином \(n\)-ной степени \[ a_n x^n + a_{n-1} x^{n-1} + \dots a_2 x^2 + a_1 x + a_0 = 0 \]
квадратный полином
\[ ax^2 + bx + c = 0 \]
- полиномы позволяют аппроксимировать закономерности любой сложности
- возможна полниномиальная регрессия (polynomial regression)
\[ y = b_0 + b_1 x + b_2 x^2 + \dots + b_{n-1}x^{n-1} + b_n x^n + e \]
Различные полиномиальные модели
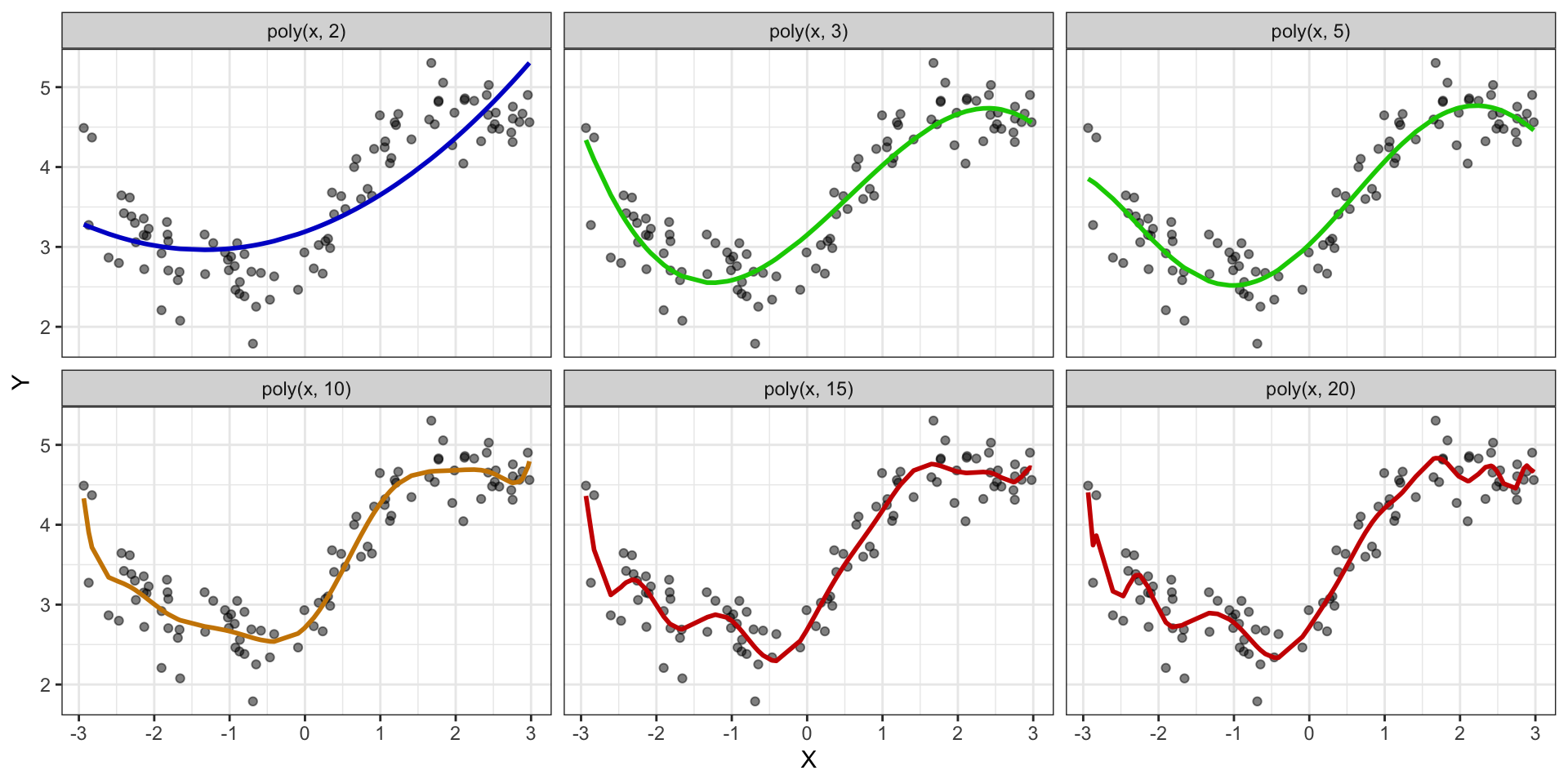
Минусы полиномиальных моделей
\[ y = b_0 + b_1 x + b_2 x^2 + \dots + b_{n-1}x^{n-1} + b_n x^n + e \]
- быстро переобучаются
- сложно интерпретировать результаты
Необходим другой способ.
Гибкие лекала

Идея GAM
\[ g(y) = b_0 + f_1(x_1) + f_2(x_2) + \dots + f_{n}x_{n} + e \]
- \(g(y)\) — функция связи
- \(f_j(x_j)\) — гладкие фукции
Идея GAM
\[ g(y) = b_0 + f_1(x_1) + f_2(x_2) + \dots + f_{n}x_{n} + e \]
- обобщенные аддитивные модели (generalized additive models, GAM)
- с помощью функций \(f_j(\cdot)\) преобразуются предикторы
- моделируется связь между преобразованными предикторами и целевой переменной
Сплайны
- работают как гибкие лекала на наших данных
- кусочно заданная функция
- на определенном диапазоне совпадает с полиномом некоторой степени
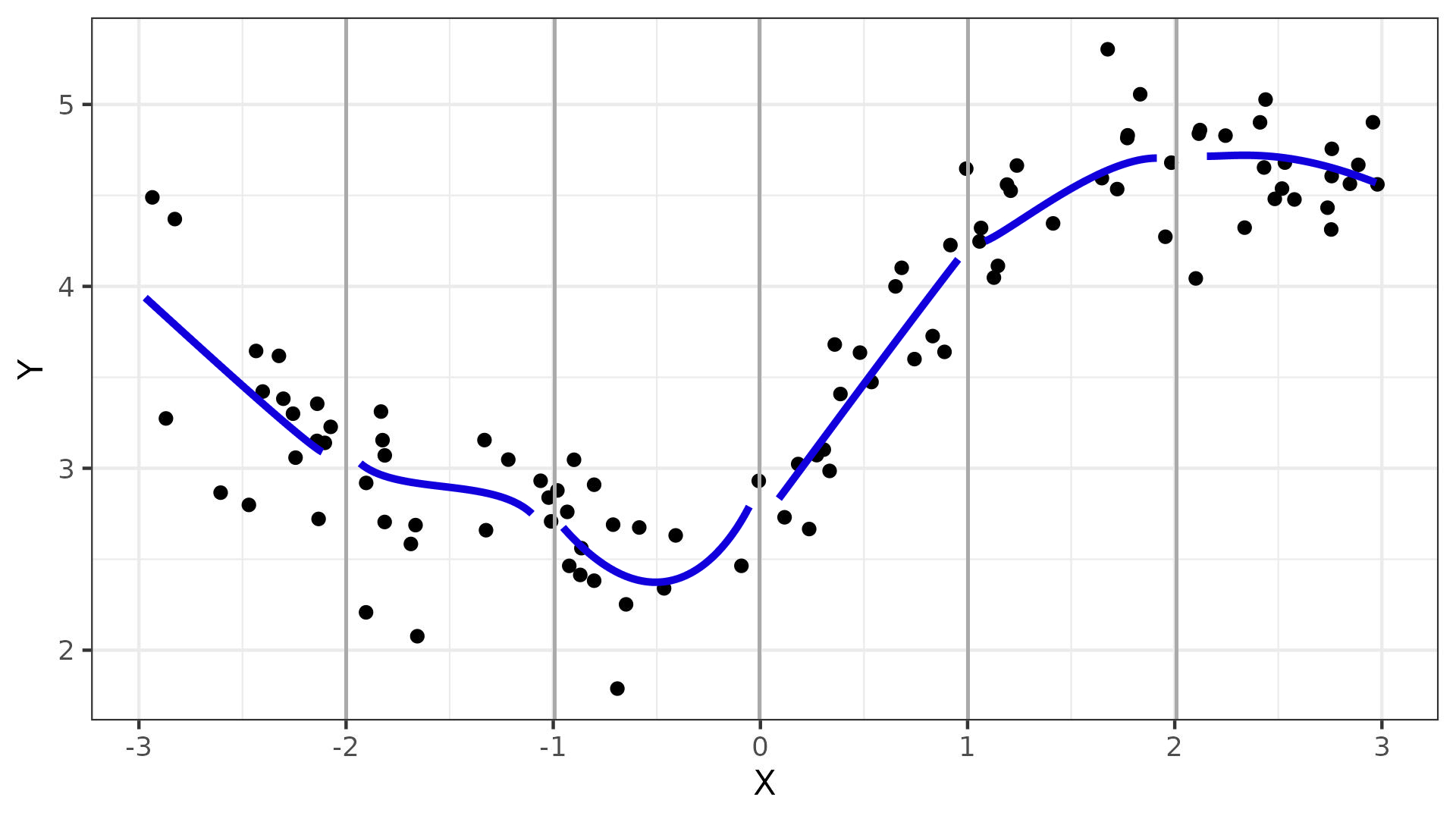
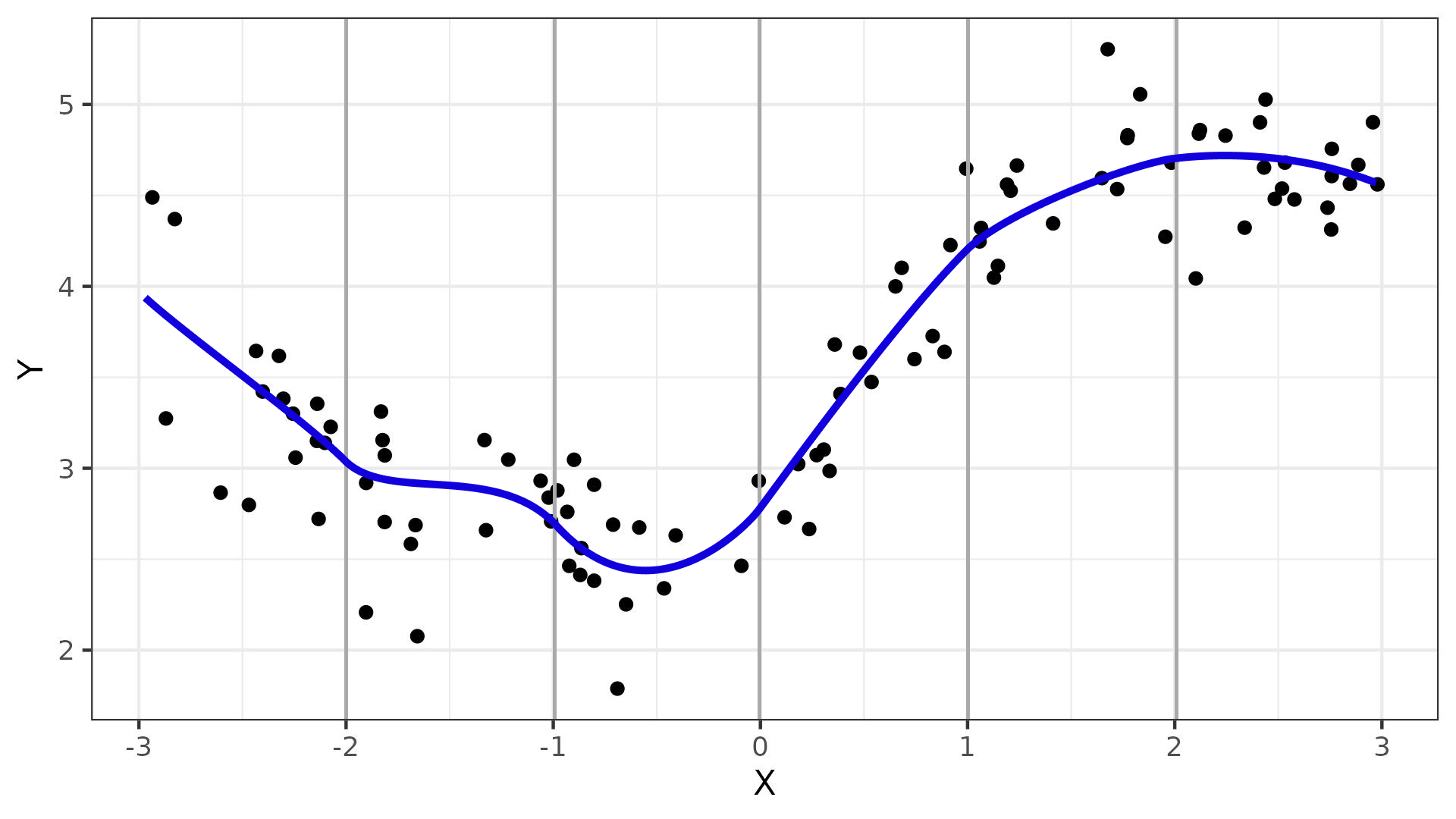
Виды сплайнов
- B-splines
- P-splines (penalized B-splines)
- cyclic splines (для циклических предикторов, например, времени)
- thin plate splines (для создания их двух предикторов одного двумерного, например, координаты)
- soap film splines
- etc.
Kernel methods
- loess (locally estimated scatterplot smoothing)
- lowess (locally weighted scatterplot smoothing)
Иерархия моделей
\[ \begin{split} \text{GAM} &\\ \downarrow &\\ \text{GLM} &\\ \downarrow &\\ \text{LM} &\\ \downarrow &\\ \text{ANOVA}& \end{split} \]
Управление детальностью
У сплайнов есть параметры:
- степень полинома
- степень сглаживания

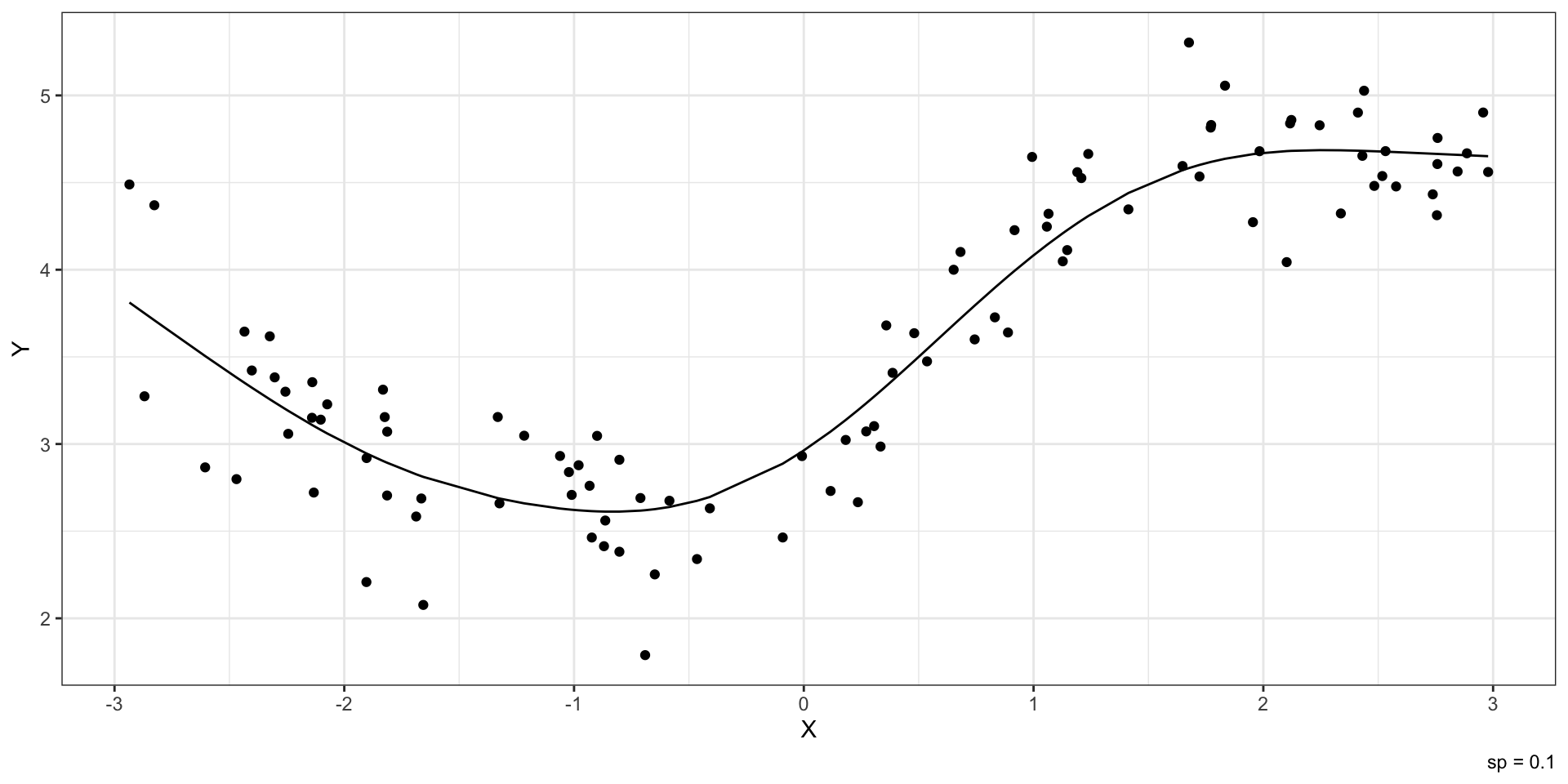
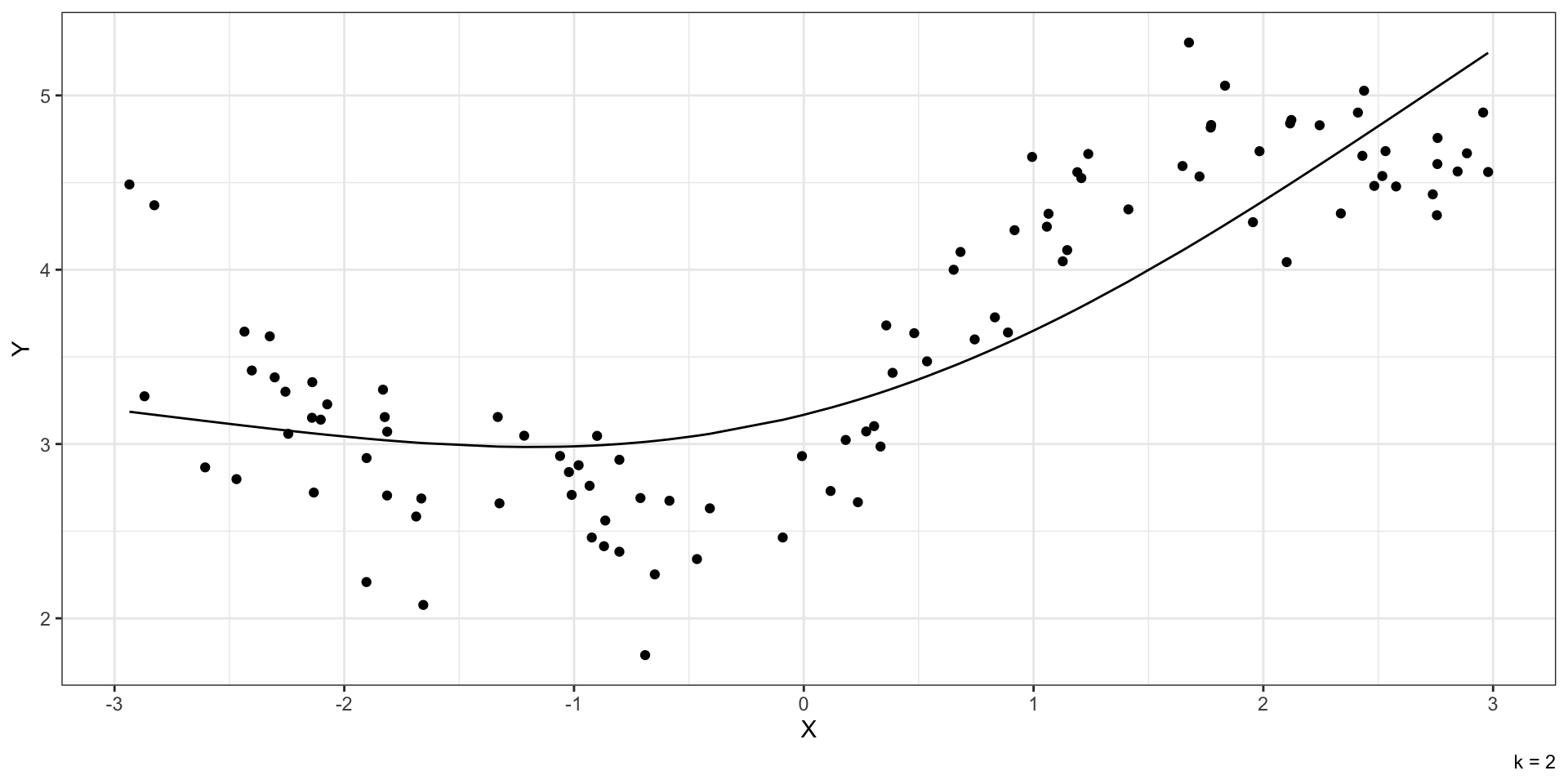
Тестирование гипотез
- коэффициентов нет, так как предиктор обернуты в функции
- протестировать гипотезы о значимость коэффициентов при количественных предикторах невозможно
- тестируются гипотезы о том, что связь между предикторов и зависимой переменной нелинейная
- коэффициенты при категориальных предикторах аналогичны линейной регрессии
- можно включить взаимодействие категориальных предикторов
Concurvity
- так как предикторы обернуты в функции, проблемы мультиколлинеарности возникнуть не может
- однако один предиктор может выражать с помощью некоторой функции через другой
- тогда возникает проблема concurvity
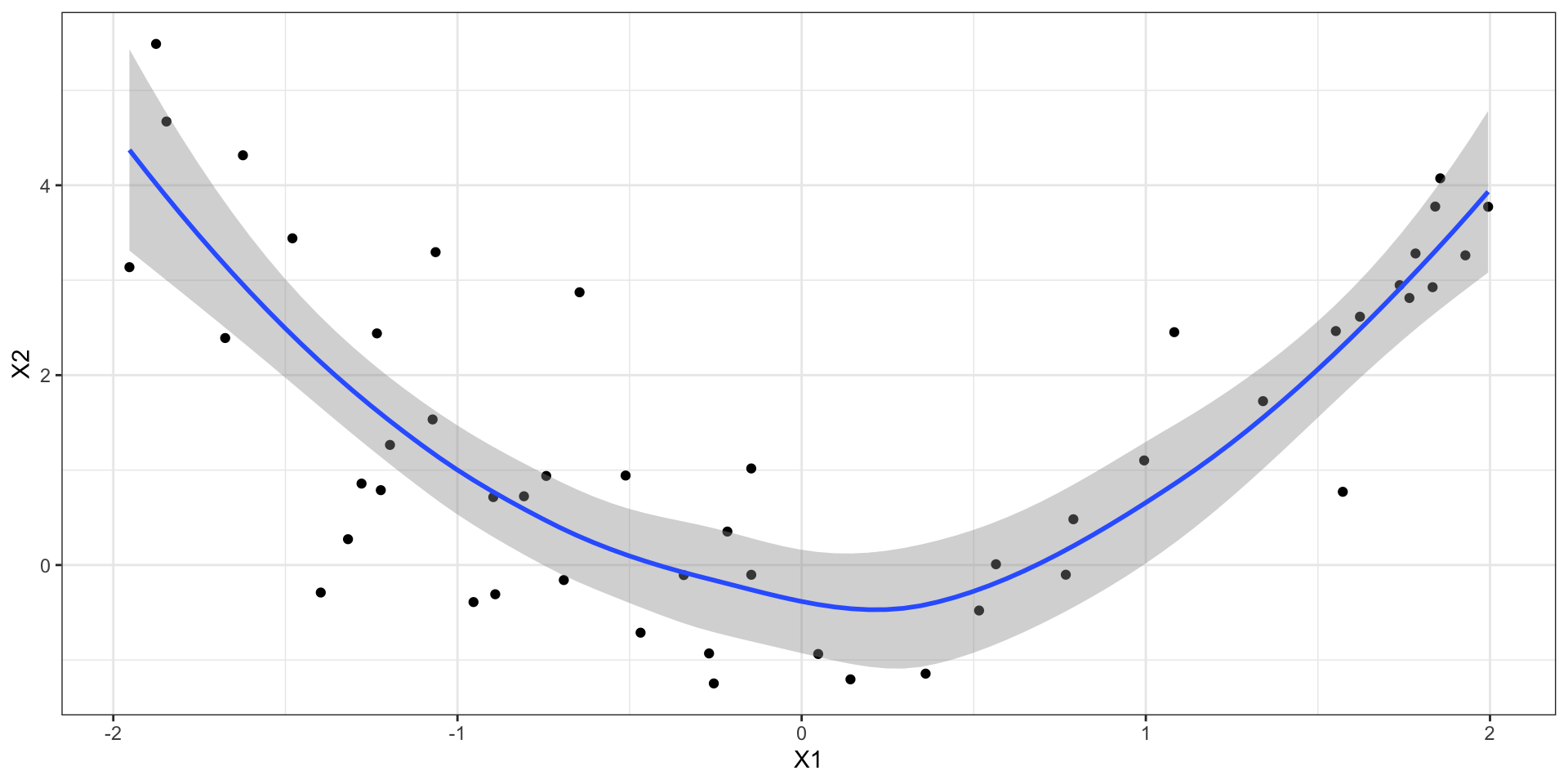
L11.2 // Регуляризация регрессии
Линейная регрессия
\[ y_i = b_0 + b_1 x_{i1} + b_2 x_{i2} + \dots + b_p x_{ip} + e_i \]
\[ \text{RSS} = \sum_{i=1}^n e_i \to \min_{\mathbf{b}} \]
- в случае мультиколлинеарности оценки коэффициентов могут быть завышены
- предлагает минимизировать не просто RSS, а RSS + штраф за оценки коэффициентов
Варианты штрафа
- Ridge-регрессия
\[ \sum_{i=1}^n e_i + \lambda \sum_{j=1}^p b_j^2 \to \min_{\mathbf{b}} \]
- LASSO-регрессия
\[ \sum_{i=1}^n e_i + \lambda \sum_{j=1}^p |b_j| \to \min_{\mathbf{b}} \]
- Метод эластичной сети (Elastic Nets)
\[ \sum_{i=1}^n e_i + \lambda_1 \sum_{j=1}^p |b_j| + \lambda_2 \sum_{j=1}^p b_j^2 \to \min_{\mathbf{b}} \]
Как это работает?
- Модель:
\[ y_i = b x_i + e_i \]
- Данные:
| \(y_i\) | \(x_i\) |
|---|---|
| \(10\) | \(1\) |
| \(20\) | \(1\) |
| \(30\) | \(2\) |
- МНК:
\[ \begin{split} \text{RSS} &= \sum_{i=1}^n (y_i - \hat y_i)^2 = \sum_{i=1}^n (y_i - bx_i)^2 = \\ &= \sum_{i=1}^n (y_i^2 - 2y_ibx_i + b^2x_i^2) = \\ &= \sum_{i=1}^n y_i^2 - 2b \sum_{i=1}^n x_iy_i + b^2 \sum_{i=1}^n x_i^2 = Q(b) \\ Q'(b) &= -2 \sum_{i=1}^n x_i y_i + 2b \sum_{i=1}^n x_i^2 = 0 \\ b_{\text{LS}} &= \frac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i^2} \\ b_{\text{LS}} &= \frac{10+20+60}{1+1+4} = \frac{90}{6} = 15 \end{split} \]
- Ridge-регрессия:
\[ \begin{split} \text{RSS} &+ \lambda b^2 \to \min_b \\ Q_\text R (b) &= \sum_{i=1}^n y_i^2 - 2b \sum_{i=1}^n x_iy_i + b^2 \sum_{i=1}^n x_i^2 + \lambda b^2 \\ Q_\text R '(b) &= -2 \sum_{i=1}^n x_i y_i + 2b \sum_{i=1}^n x_i^2 + 2 \lambda b = 0 \\ b_{\text{R}} &= \frac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i^2 + \lambda} \\ b_{\text{R}} &= \frac{90}{6 + \lambda} \\ \lambda & = 100: b_{\text{R}} = \frac{90}{6 + 100} < 1 \end{split} \]
Особенности регуляризованной регрессии
- с ростом штрафного коэффициента \(\lambda\) значения коэффициентом стремятся к нулю
- необходимо найти баланс между штрафом и количеством коэффициентов, которое нам необходимо для описания закономерности
- введение штрафного коэффициента лишает нас возможности тестирования статистические гипотезы
Итоги
- GAM — самые обобщенные модели
- гладкие функции и сплайны
- возможности и ограничения GAM
- регуляризация регрессии через штрафной коэффициент
- точное моделирование взамен проверки гипотез
L11 // Регуляризация регрессии. Обобщенные аддитивные модели
Антон Ангельгардт

WLM 2023