L12 // Линейные модели со смешанными эффектами
Что будет?
- Ограничения обобщенных линейных моделей
- Случайные и фиксированные факторы
- Подбор коэффициентов модели
- Диагностика моделей
- Тестирование гипотез
- Дальнейшее расширение смешанных моделей
Ограничения изученных ранее линейных моделей
- в общих и обобщенных линейных моделях предполагается независимость наблюдений
- данные могут иметь некоторую группировку (clustered data)
- разные периоды времени
- разных участках пространства
- повторные измерения
- измерения на разных группах испытуемых / респондентов
Внутригрупповые корреляции (intraclass correlations) — наблюдения из одной группы более похожи друг на друга, чем наблюдениях из разных групп.
Что делать?
- Структуру данных нельзя игнорировать — увеличивается вероятность ошибиться с выводами
- Включить группирующие факторы в модель в качестве предикторов?
- усложняется модель (чрезмерно увеличивается количество параметров),
- широту обобщения результатов огранчена
Решение: введение в модель случайных факторов.
Случайные vs фиксированные факторы

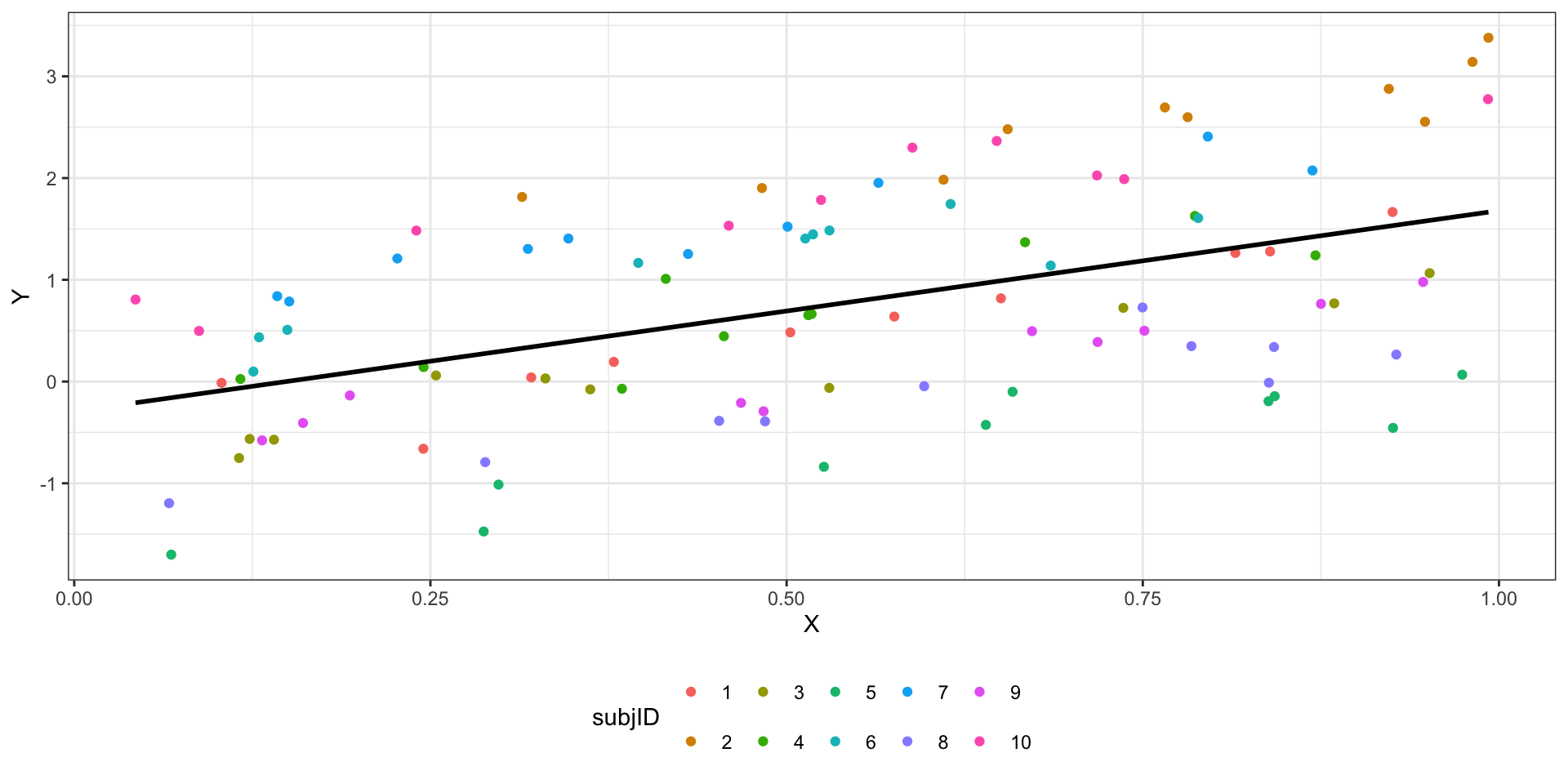
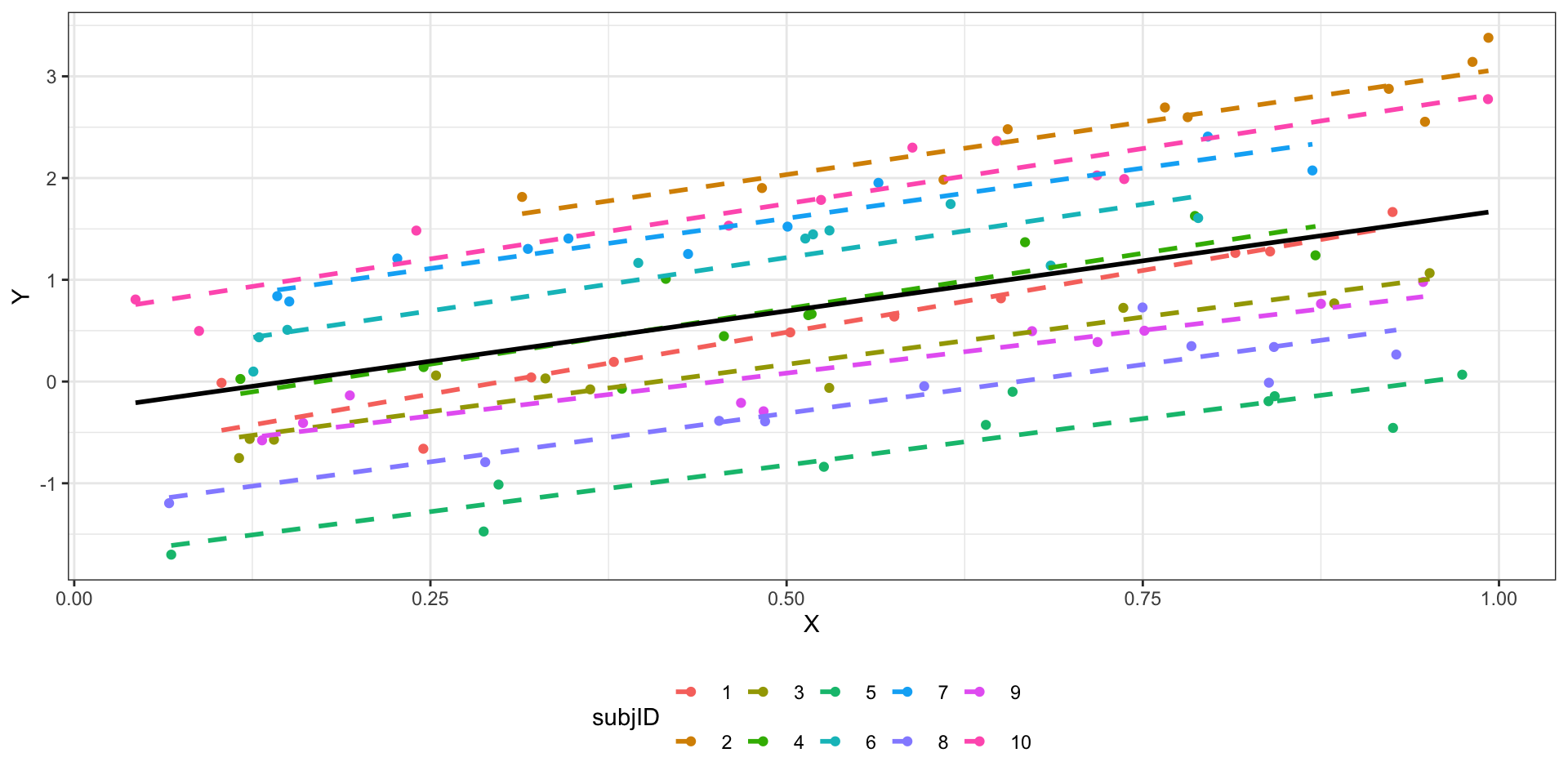
Случайные vs фиксированные факторы
| Свойства | Фиксированные факторы | Случайные факторы |
|---|---|---|
| Уровни фактора | Фиксированные, заранее определенные, потенциально воспроизводимые | Случайная выборка из всех возмоных уровней |
| Используются для тестирвоания гипотез | О средних значения ЗП на раных уровнях фактора \(H_0:\mu_1 = \mu_2 = \dots = \mu\) | О дисперсии ЗП между уровнями фактора \(H_0:\sigma_r^2 = 0\) |
| Выводы можно экстраполировать | Только на уровни анализа | На все возможные уровни |
Виды GLMM и их математическая формулировка
- Модель со случайным интерсептом
\[ \begin{split} y_{ij} &= \beta_0 + \beta_1 x_{ij} + \eta_i + \varepsilon_{ij} \\ \eta_i &\thicksim \mathrm{N} (0, \sigma^2_\eta) \\ \varepsilon_i &\thicksim \mathrm{N} (0, \sigma^2) \end{split} \]
\(i\) — наблюдение (респондент), \(j\) — уровни (значения) предиктора.
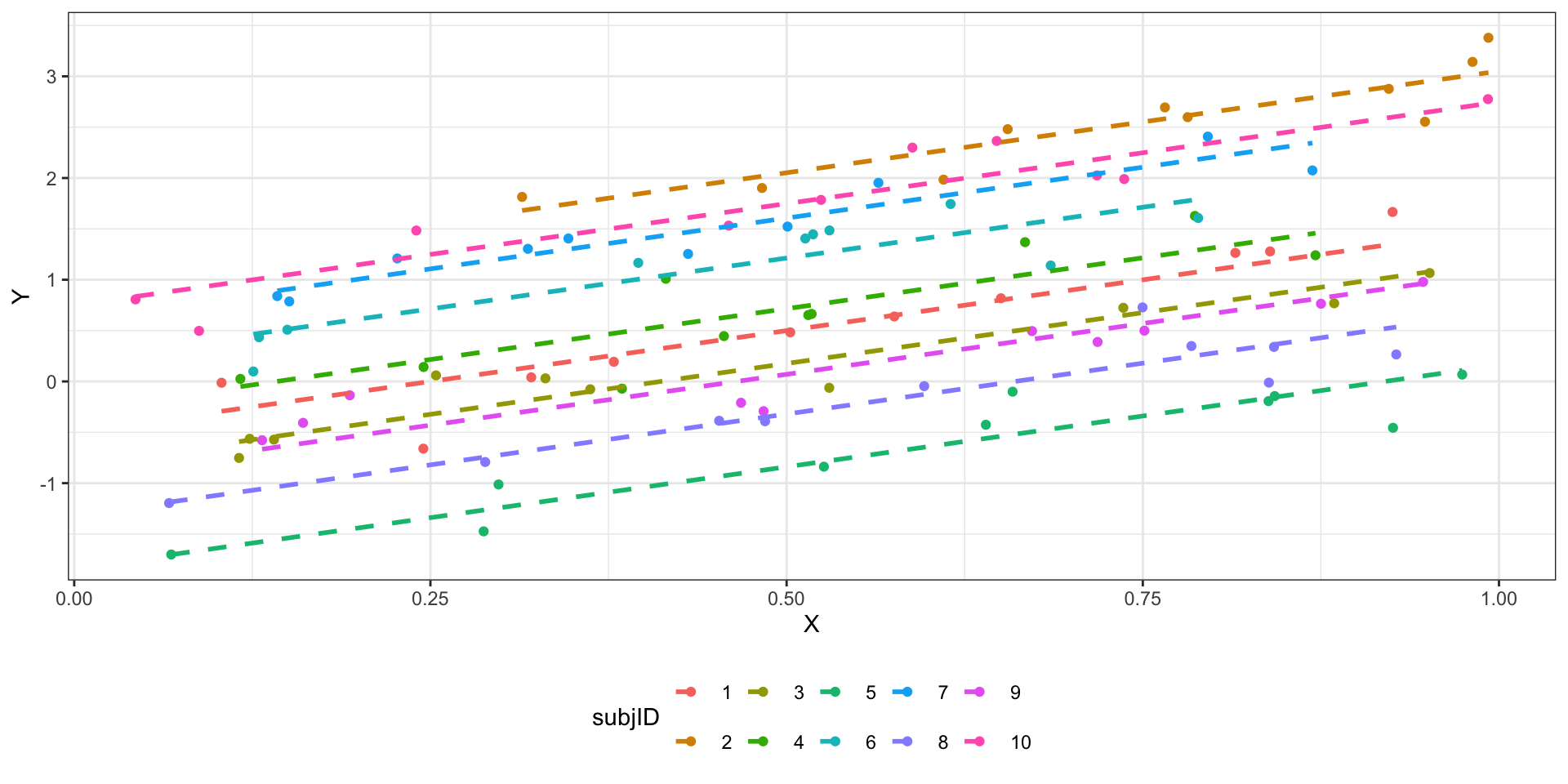
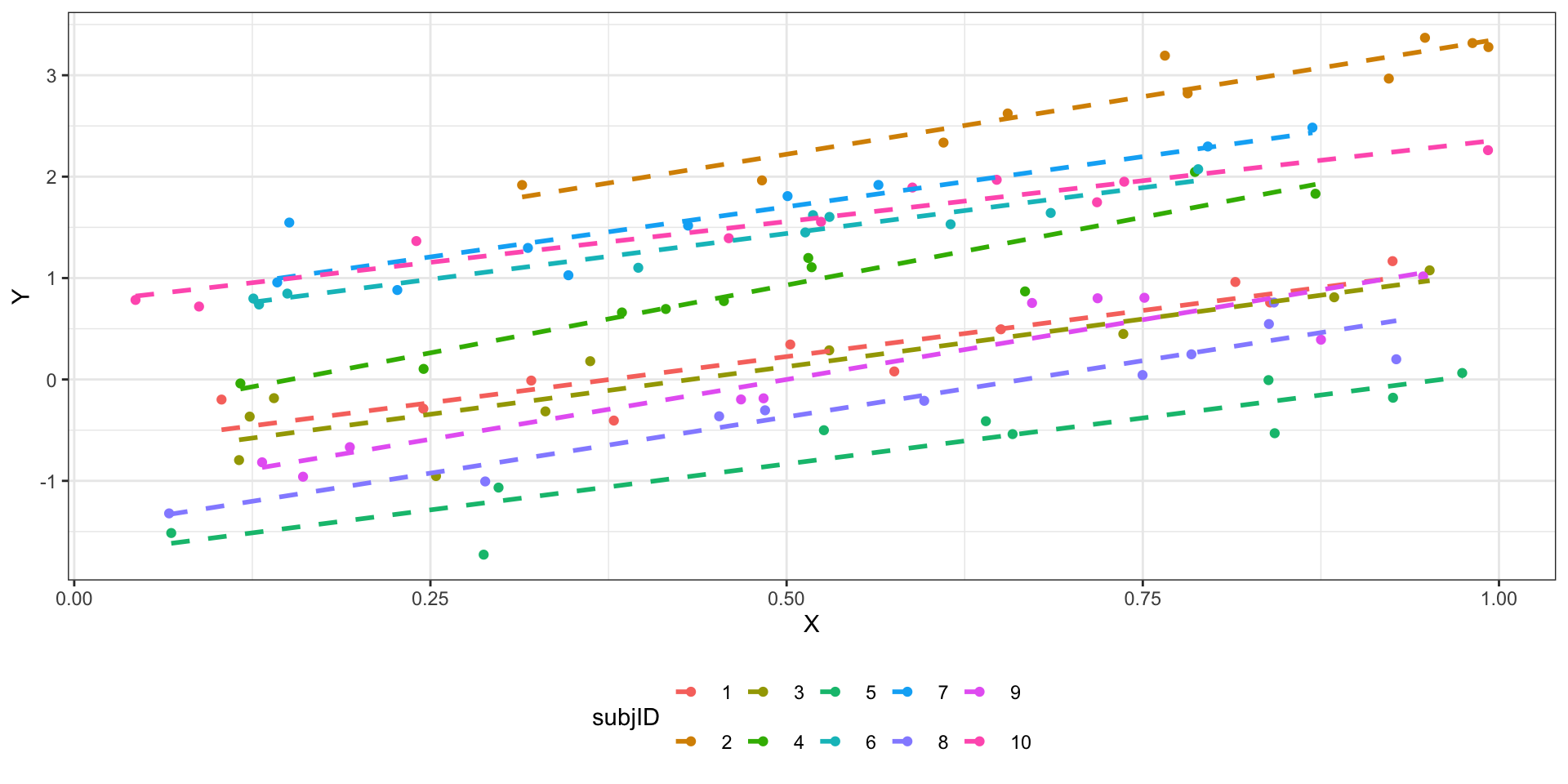
- Модель со случайным интерсептом и углом наклона
\[ \begin{split} y_{ij} &= \beta_0 + \beta_1 x_{ij} + \eta_{0i} + \eta_{1ij} x_{ij} + \varepsilon_{ij} \\ \eta_{0i} &\thicksim \mathrm{N} (0, \sigma^2_{\eta_0}) \\ \eta_{1ij} &\thicksim \mathrm{N} (0, \sigma^2_{\eta_1}) \\ \varepsilon_{ij} &\thicksim \mathrm{N} (0, \sigma^2) \end{split} \]
\(i\) — наблюдение (респондент), \(j\) — уровни (значения) предиктора.
Методы подбора параметров в смешанных моделях
- метод максимального правдоподобия (maximum likelihood, ML)
- оценка дисперсии методом максимального правдоподобия приводит к смещенным оценкам
- так как сразу приходится оценивать и \(\beta\), и дисперсии
- метод ограниченного максимального правдоподобия (restricted maximum likelihood, REML)
- с помощью математических преобразований зануляются \(\beta\)
- получаются несмещенные оценки дисперсий
REML-оценки \(\beta\) стремятся к ML-оценкам при увеличении объема выборки.
Что использовать?
- Для точных оценок фиксированных эффектов — ML.
- Для точных оценок случайных эффектов — REML.
- При работе с правдоподобиями в моделях, подобранных REML, должна быть одинаковая фиксированная часть.
- Для обобщенных негауссовских смешанных линейных моделей REML не определен — используется ML.
Диагностика модели
- коэффициент внутриклассовой корреляции (intra-class correlation, ICC)
\[ \eta \thicksim \mathrm{N} (0, \sigma^2_\eta) \]
\[ \varepsilon \overset{\text{i.i.d}}{\thicksim} \mathrm{N} (0, \sigma^2) \]
\[ \text{ICC} = \frac{\sigma^2_\eta}{\sigma^2_\eta + \sigma^2} \]
- Если ICC низкий, то наблюдения очень разные внутри каждой из групп. Значит, чтобы надежно оценить эффект этого случайного фактора, нужно брать больше наблюдений в группе.
- Если ICC высокий, то наблюдения очень похожи внутри каждой из групп, заданных случайным фактором. Значит, можно брать меньше наблюдений в группе.
Pseudo-\(R^2\)
- Marginal \(R^2\) — доля дисперсии, объясненной фиксированными факторами
- Conditional \(R^2\) — доля дисперсии, объясненной моделью в целом (и фиксированными, и случайными факторами)
Анализ остатков модели
- линейность связи
- распределение остатков
- (не)зависимость остатков от предсказанных значений
- зависимость остатков от случайных факторов
Тестирование гипотез
- t-тесты Вальда
\[ \begin{split} &H_0: \beta_k = 0 \\ &H_1: \beta_k \neq 0 \\ t &= \frac{b_k - \beta_k}{\text{se}_{b_k}} = \frac{b_k}{\text{se}_{b_k}} \thicksim t(n-p) \end{split} \]
- тесты отношения правдоподобий
\[ \text{LRT} = 2 \ln \Big( \frac{L_{\text{M}_1}}{L_{\text{M}_2}} \Big ) = 2 (\ln L_{\text{M}_1} - L_{\text{M}_2}) \]
- LRT для случайных эффектов
- модели с одинаковой фиксированной частью, подобранные REML
- уровни значимости будут завышены
- обычно тесты не делают, а набор случайных эффектов определяется структурой данных
- LRT для фиксированных эффектов
- модели с одинаковой случайной частью, подобранные ML
- уровни значимости будут занижены
Сравнение моделей
- тесты отношения правдоподобий
- информационные критерии (AIC, BIC)
Модели для других распределений
Совместив идеи GLM и mixed models можно получить модели для бинарных переменных.
- В основе — подбор параметров логистической регрессионной модели
- Параметры подбираются методом максимального правдоподобия
- Угловые коэффициенты — во сколько раз изменяется соотношение шансов для события при увеличении предиктора на единицу
- Группирующие факторы — дисперсия свободного члена модели или дисперсия углового коэффициента
- Внутриклассовые корреляции — приблизительные
- Если ICC равен нулю, стоит отказаться от случайных факторов и применить обычную GLM
Аналогично можно получить смешанные модели для счетных переменных.
Итоги
- Зависимость наблюдений нужно учитывать
- Сделать это можно введением случайных факторов в модель
- Существует случайный интерсепт и случайный угловой коэффициент
- REML работает на случайные эффекты, ML — на фиксированные
- Диагностика как и раньше, но шире
- Тестирование гипотез аналогично GLM
- Возможны модели для других распределений целевой переменной
L12 // Линейные модели со смешанными эффектами
Антон Ангельгардт

WLM 2023