L13 // Кластерный анализ

Антон Ангельгардт

Зачем?

Поиск структуры в данных
Кластеры и задача кластеризации
Четкая кластеризация — иерархическая и k-means
Нечеткая кластеризация — C-means

Регрессия, классификация, кластеризация

задача регрессии — выяснить влияние определенных факторов на количественную переменную и предсказать её значение
задача классификации — определить, к какому классу относиться объект
задача кластеризации — определить, какие наблюдения похожи друг на друга, то есть разбить их на группы, при условии что группы неизвестны.

Геометрическая интерпретация задачи кластеризации

каждый из \(n\) рассматриваемых объектов — это точка в некотором \(p\)-мерном признаковом пространстве;
похожие объекты будут располагаться «близко» друг с другу;
различающиеся объекты будут располагаться «далеко» друг от друга;
скопления точек — это искомые кластеры.

Проблема кластеризации

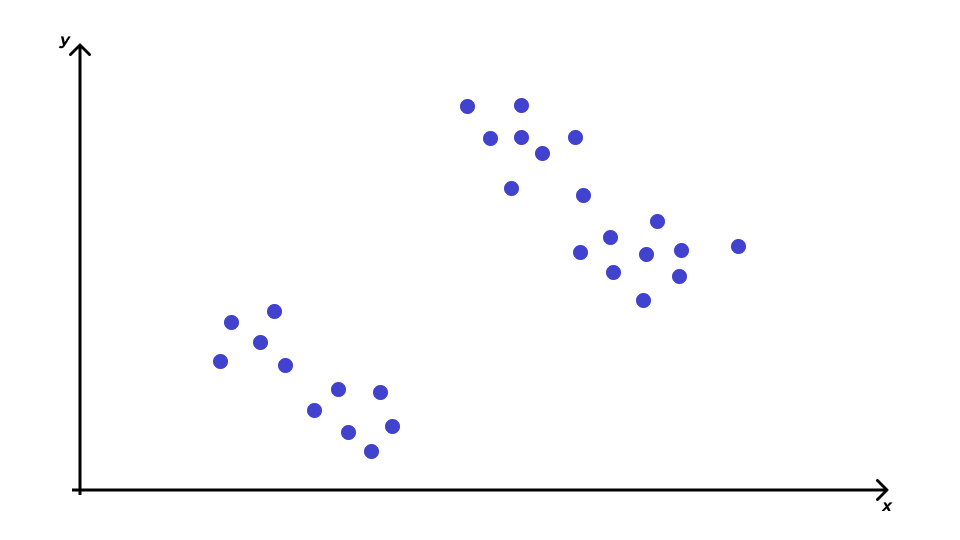
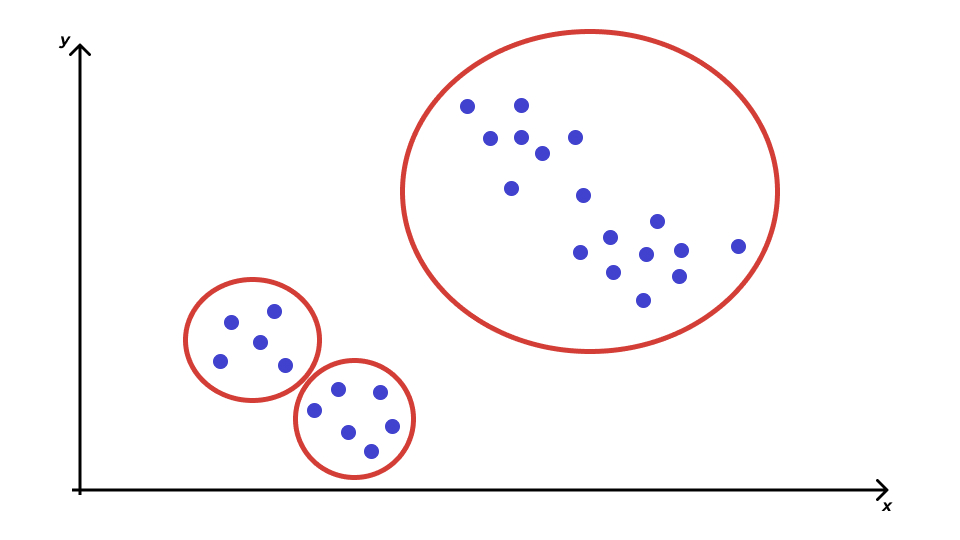
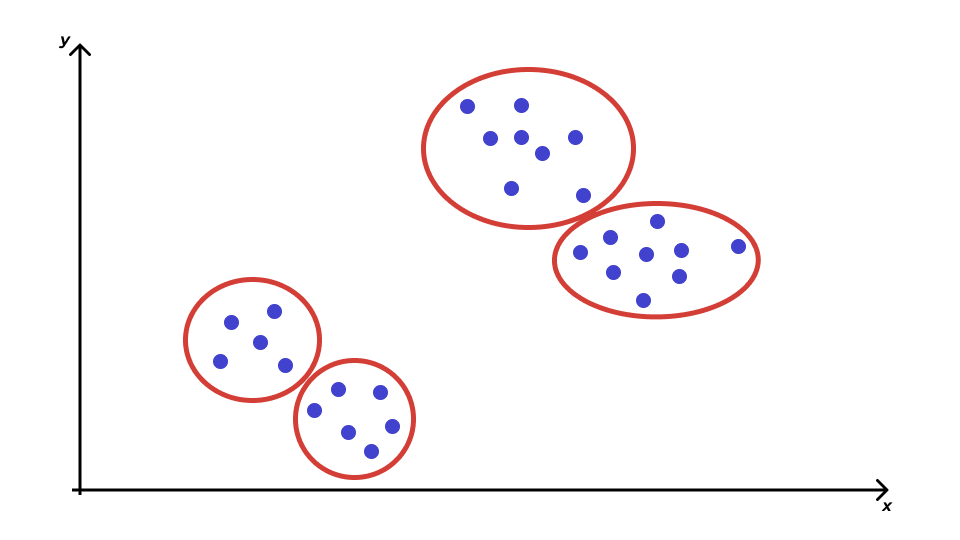
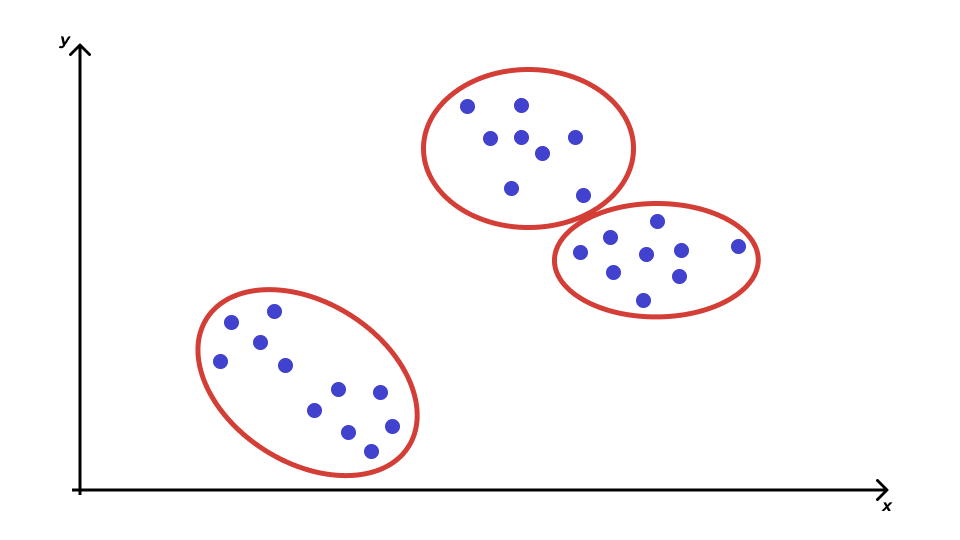
Расстояние между объектами

Евклидово расстояние

\[ d_{\text{Eucl},XY} = \sqrt{\sum_{j=1}^p (x_j - y_j)^2} \]

Манхэттеновское расстояние

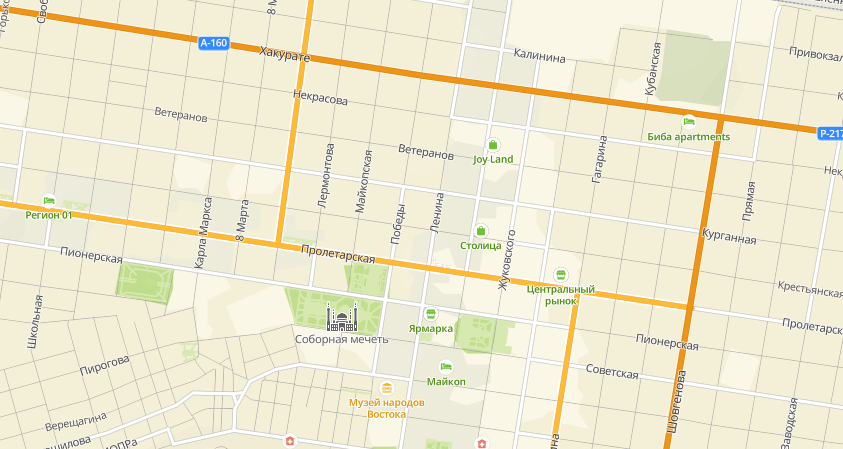
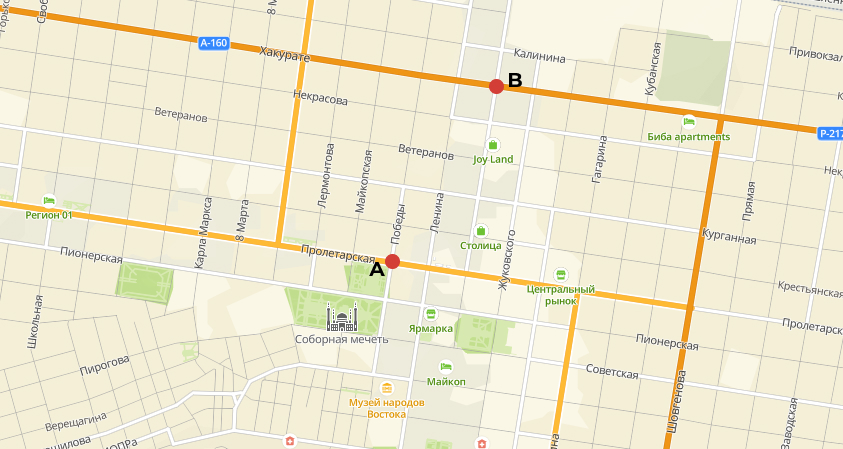
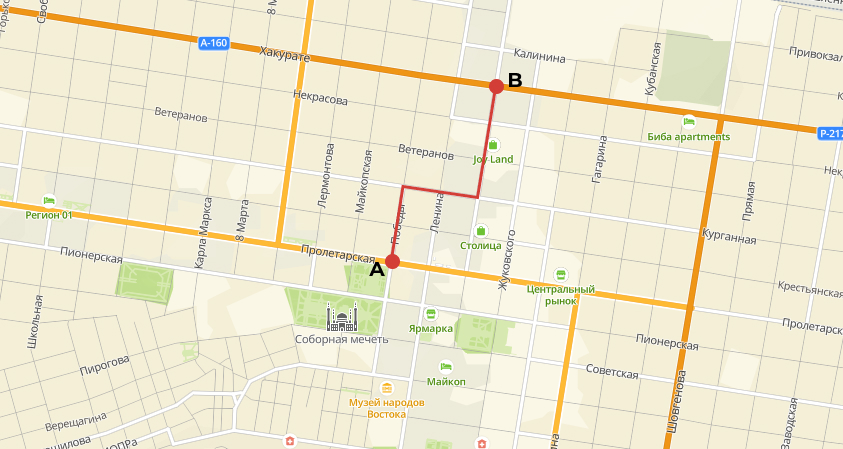
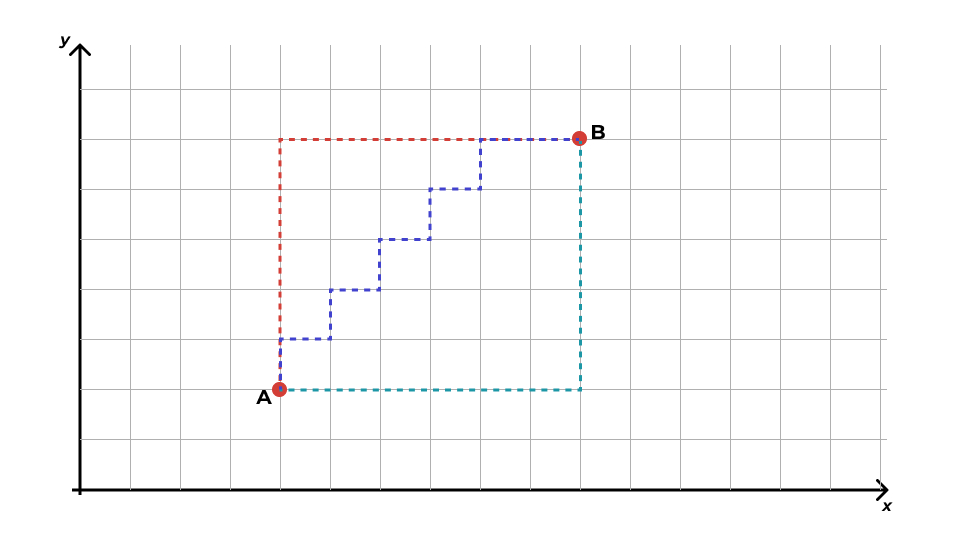
\[ d_{\text{Manh},XY} = \sum^p_{j=1} |x_j - y_j| \]

Евклид vs Манхэттен

Если большая разница значений по одной из переменных достаточным основанием для отнесения наблюдений к различным кластерам, то можно использовать такое расстояние. Если нет, то Манхэттен.
Если переменные непрерывные, то можно использовать евклидово расстояние. Если переменные дискретные, то манхэттеновское расстояние.

Проблема операционализации расстояния

Хотим кластеризовать наших испытуемых на «эффективных решателей задачи» и «неэффективных решателей задачи»
- время решения и число ошибок в ходе решения
- как мы будем замерять эти переменные?
Как нам кластеризовать менеджеров на «хороших», «плохих» и «средненьких продажников»?
- можем использовать разные подходы: оценку 360, показатели KPI и т. д.
Как определять расстояние между сайтами?

Субъективность кластерного анализа

отбор переменных для анализа
какие переменные включать в анализ? все? или необходимо проводить отбор?
возможно наличие переменных, которые будут хорошо работать с точки зрения поиска схожих объектов, но это не то сходство, которое мы ищем
одни переменные могут быть косвенно заменены другими (уровень дохода — профессия, образование, стаж работы)
«ковариаты» могут быть важны при формировании кластеров (число учащихся и учителей в школах)
правильный выбор переменных крайне важен
критерием при отборе переменных выступает ясность интерпретации полученного результата и «интуиция исследователя»
метод стандартизации
выбор метрики для расстояния между объектами
выбор метрики для расстояния между кластерами
[иногда] определение числа кластеров
интерпретация результатов

Расстояние между кластерами

среднее невзвешенное расстояние (average linkage clustering)

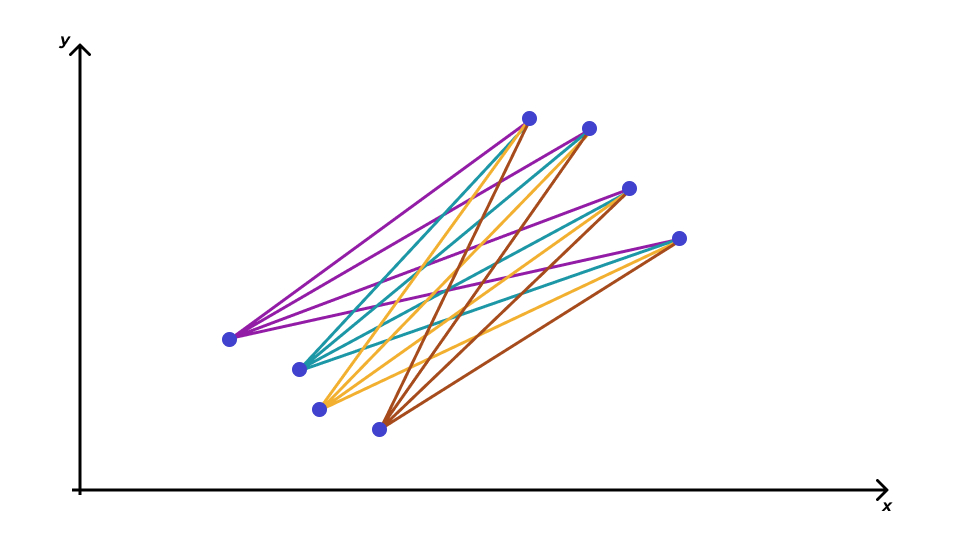
центроидный метод

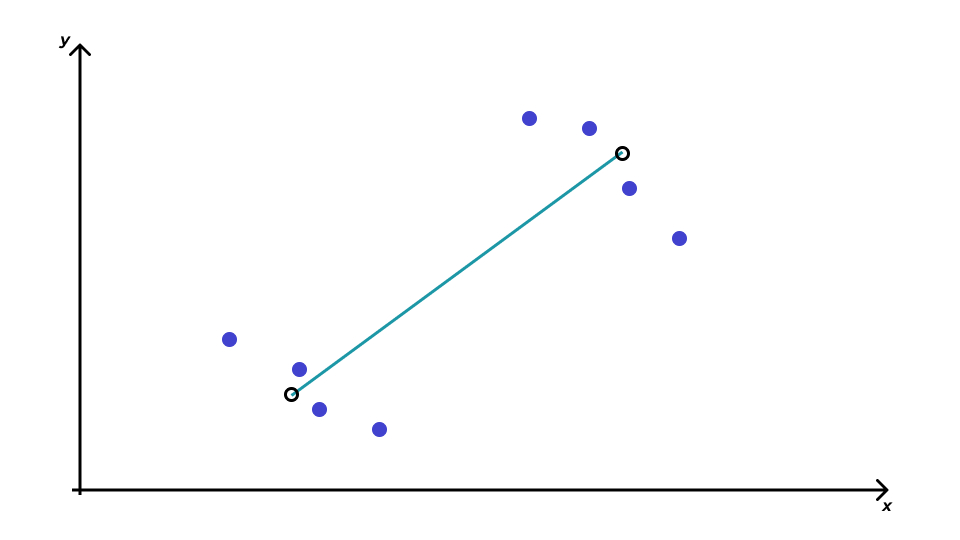
метод дальнего соседа

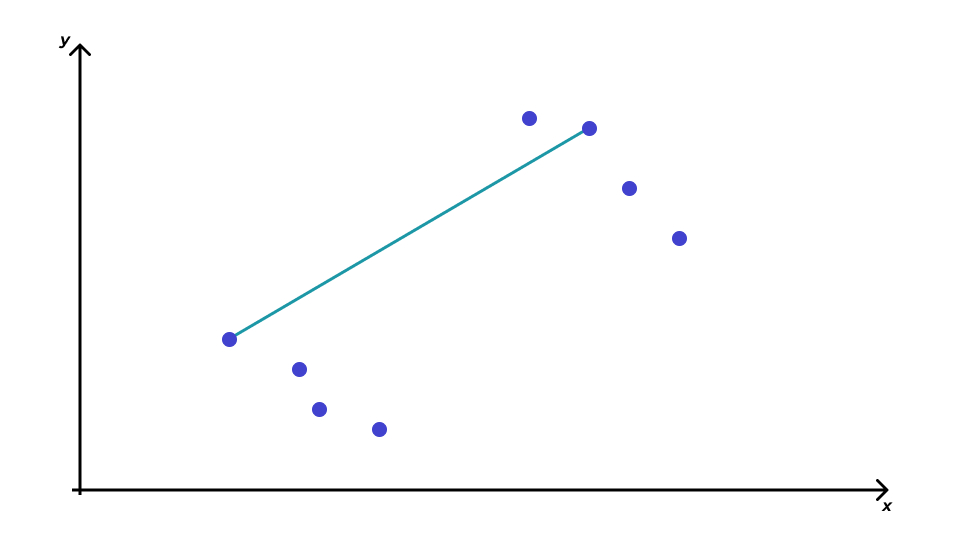
метод ближайшего соседа

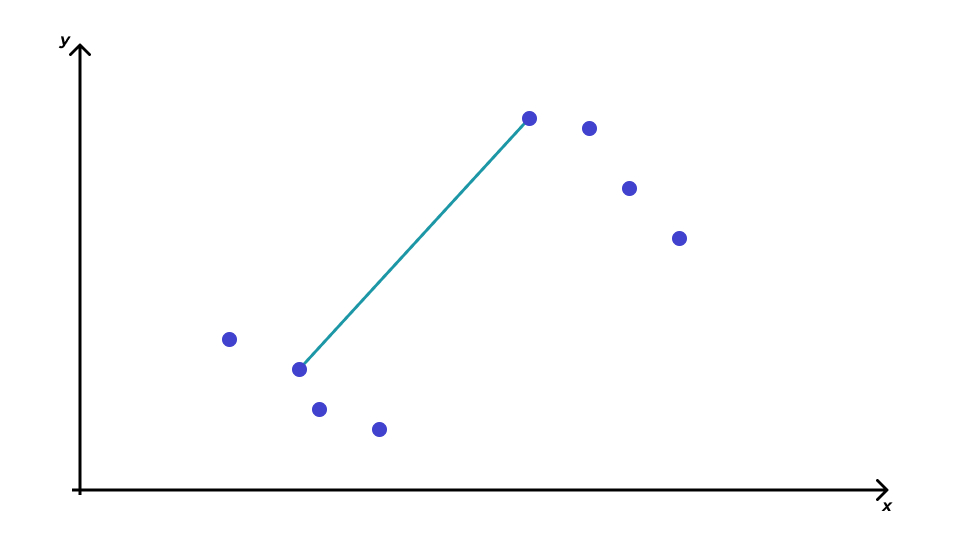
Иерархическая кластеризация

Алгоритм иерархического кластерного анализа

Каждый объект объявляется кластером — из \(n\) наблюдений получается \(n\) кластеров.
Выбираются два ближайших кластера — они объединяются.
Выбираются два ближайших кластера — они объединяются [2].
Выбираются два ближайших кластера — они объединяются [3].
Так происходит до тех пор, пока не остается два кластера.
Оставшиеся два кластера являются ближайшими друг с другу — поэтому объединяются в один.

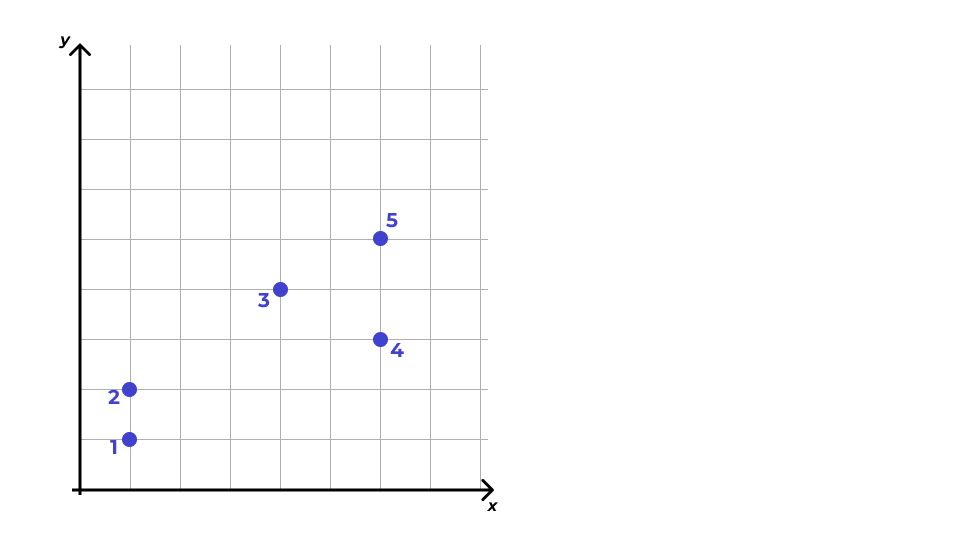
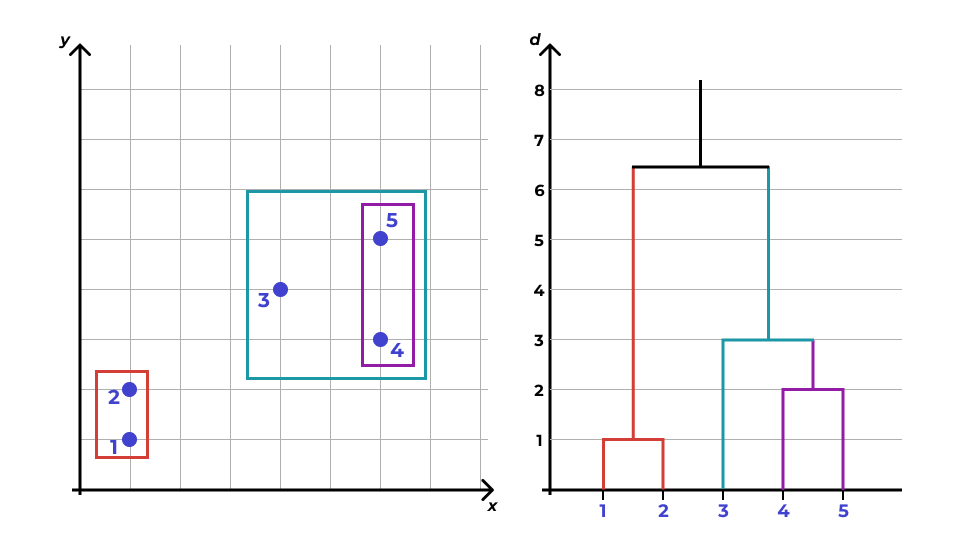
Дендрограмма

На прямой располагаются все наблюдения как отдельные кластеры.
Каждому кластеру соответствует вертикальная линия.
Каждому объединению кластеров соответствует горизонтальная линия.
Высота, на которой кластеры соединяются, отражает расстояние между кластерами.

Каменистая осыпь

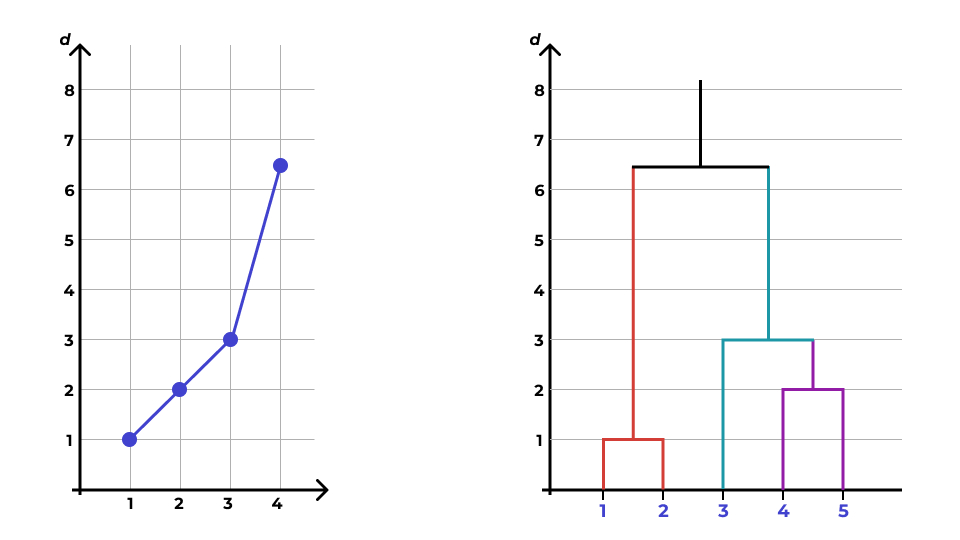
Когда кластеризации нет?

паттерны дендрограммы и каменистой осыпи могут быть крайне разнообразны
если кластеризаци нет, то отсутствует скачок расстояний на дендрограмме и излом линии на графике «каменистая осыпь»

Метод k-средних (k-means)

Алгоритм метода k-средних

Заранее определяется число кластеров \(k\). Хотя вообще-то это невозможно, однако уже найдены способы, чтобы обойти это ограничение.
Для анализа выбирается \(k\) точек — центры кластеров.
Объект приписывается к тому кластеру, чей центр ближайший.
Центр кластера — центр тяжести объектов кластера.

центр тяжести множества точек с координатами \((x_{i1}, x_{i2}, \dots, x_{ip})\) — это точка с координатами \((\bar x_1, \bar x_2, \dots, \bar x_p)\).

Повторяем поочерёдно пункты 3 и 4 до тех пор, пока центры кластеров не перестанут двигаться.

Визуализацию можно посмотреть тут.

Ограничения k-means

Необходимо заранее определить число кластеров
Используется только евклидово растояние
- хотя этот недостаток исправляется в других модификациях метода
Результат зависит от начальных центров кластеров

Начальное положение кластеров

Forgy — Случайным образом выбираются \(k\) наблюдений. Они объявляются начальными центрами кластеров.
Случайное разбиение (Random Partition) — Каждое наблюдение случайным образом приписывается к одному из кластеров. Находятся центры тяжести кластеров. Они объявляются начальными центрами кластеров.

Метрики качества кластеризации

Компактность кластеров (cluster cohesion)

\[ \text{WSS} = \sum_{j=1}^k \sum^{|C_j|}_{i=1} (x_{ij} − \bar x_j)^2, \]

где \(k\) — число кластеров, \(|C_j|\) — количество объектов в данном кластере.

Отделимость кластеров (cluster separation)

\[ \text{BSS} = n \cdot \sum_{j=1}^k (\bar x_j - \bar x)^2, \]

где \(k\) — число кластеров.

Нечеткая кластеризация

k-means и иерархическая кластеризаци приписывают каждому наблюдению некоторый единственный кластер — чёткая кластеризация
метод C-средних (C-means) позволяет разбить наблюдения на заданное число \(k\) нечетких кластеров
рассчитывается степень принадлежности (membership value) наблюдения к каждому из кластеров

Алгоритм C-means

Каждому наблюдению присваивается случайное число, задающее его принадлежность к кластеру.

Кластер	\((1,3)\)	\((2,5)\)	\((4,8)\)	\((7,9)\)
1	0.8	0.7	0.2	0.1
2	0.2	0.3	0.8	0.9

Вычисляются центры (центроиды) кластеров.

\[ V_{ij} = \frac{\sum_{k=1}^n \gamma_{ik}^m x^{(j)}_k}{\sum_{k=1}^n \gamma_{ik}^m}, \]

где \(\gamma\) — membership value, \(m\) — fuzziness parameter (степень нечеткости кластеров, стандартное значение — от 1.2 до 2), \(x^{(j)}_k\) — координата наблюдения, \(i\) — номер кластера, \(j\) — номера координаты.

Для представленной таблицы координаты центроидов будут таковы:

\[ \begin{split} \mathbf{V}_1 &= (V_{11}, V_{12}) = (1.568, 4.051) \\ \mathbf{V}_1 &= (V_{21}, V_{22}) = (5.350, 8.215) \end{split} \]

Расчитываются расстояния от каждого наблюдения до центров (центроидов) кластеров.

Если использовать евклидово расстояние, то для рассматриваемого примера они будут такими:

Кластер	\((1,3)\)	\((2,5)\)	\((4,8)\)	\((7,9)\)
1	\(d_{11} = 1.2\)	\(d_{21} = 1.04\)	\(d_{31} = 4.63\)	\(d_{41} = 7.34\)
2	\(d_{12} = 6.79\)	\(d_{22} = 4.64\)	\(d_{32} = 1.36\)	\(d_{42} = 1.82\)

Обновляются значения membership values для наблюдений по следующей формуле:

\[ \gamma_{pi} = \Bigg( \sum_{j=1}^J \Big( \frac{d_{pi}^2}{d_{pj}^2} \Big) ^{\frac{1}{m-1}} \Bigg)^{-1}, \]

где \(i\) — номер кластера, \(p\) — номер наблюдения, \(d\) — расстояние между наблюдением и центром кластера, \(J\) — количество кластеров, \(m\) — fuzziness parameter.

В рассматриваемом примере получатся такие значения:

Кластер	\((1,3)\)	\((2,5)\)	\((4,8)\)	\((7,9)\)
1	0.97	0.95	0.08	0.06
2	0.03	0.05	0.92	0.94

Повторяются шаги 2–4 до тех пор, пока значения membership values не перестанут меняться.

По полученой таблице и определяется структура данных — или её отсутствие.

Итоги

Кластеры и расстояния
Иерархическая кластеризация
Дендрограмма и каменистая осыпь
k-means
c-means

L13 // Кластерный анализ

Антон Ангельгардт