L14 // Анализ главных компонент. Эксплораторный факторный анализ

Антон Ангельгардт

Что будет?

проблема большого количества переменных
модели PCA и EFA
главные компоненты и факторы
решение задачи факторного анализа

Проклятие размености (curse of dimensionality)

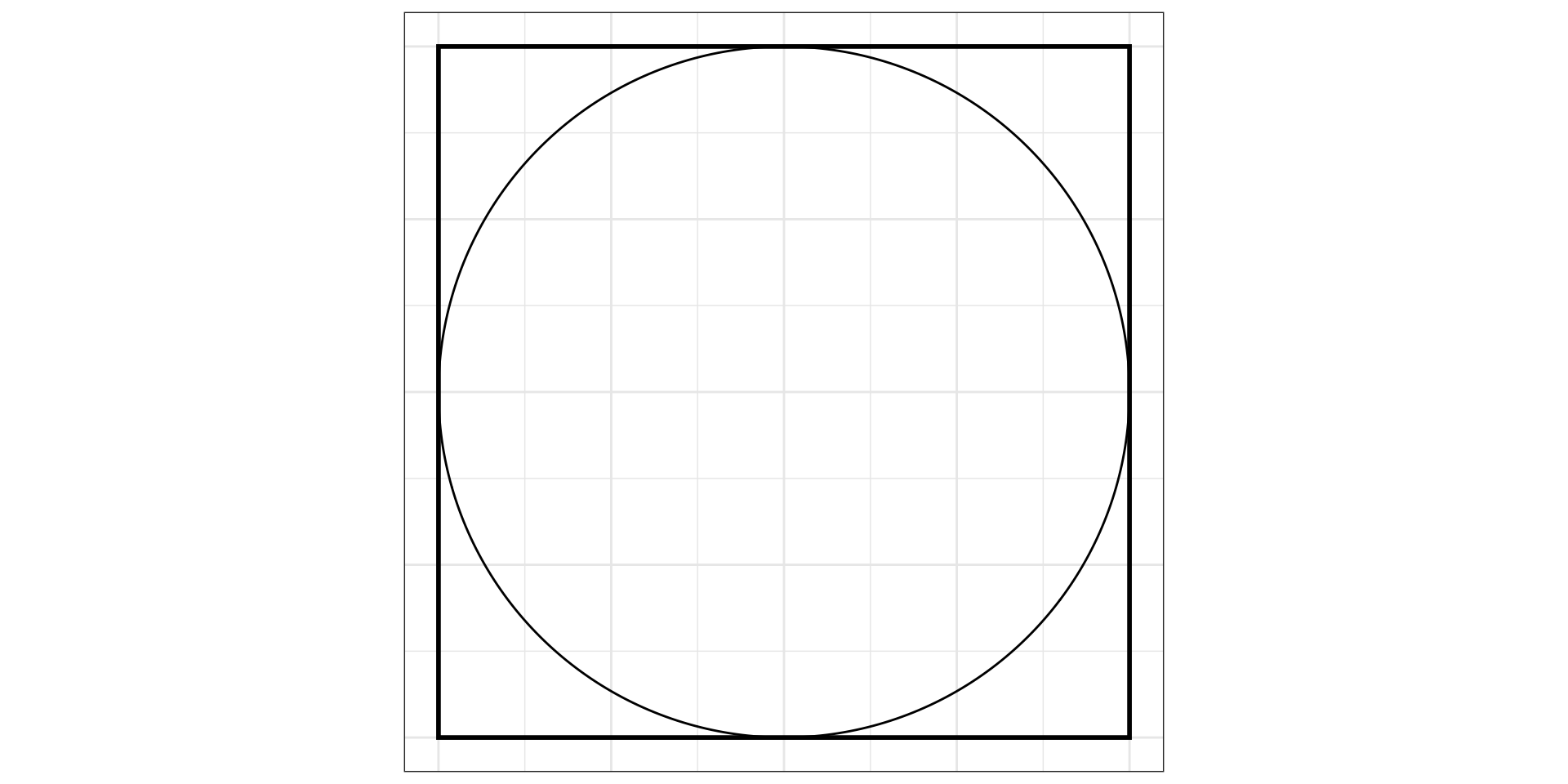
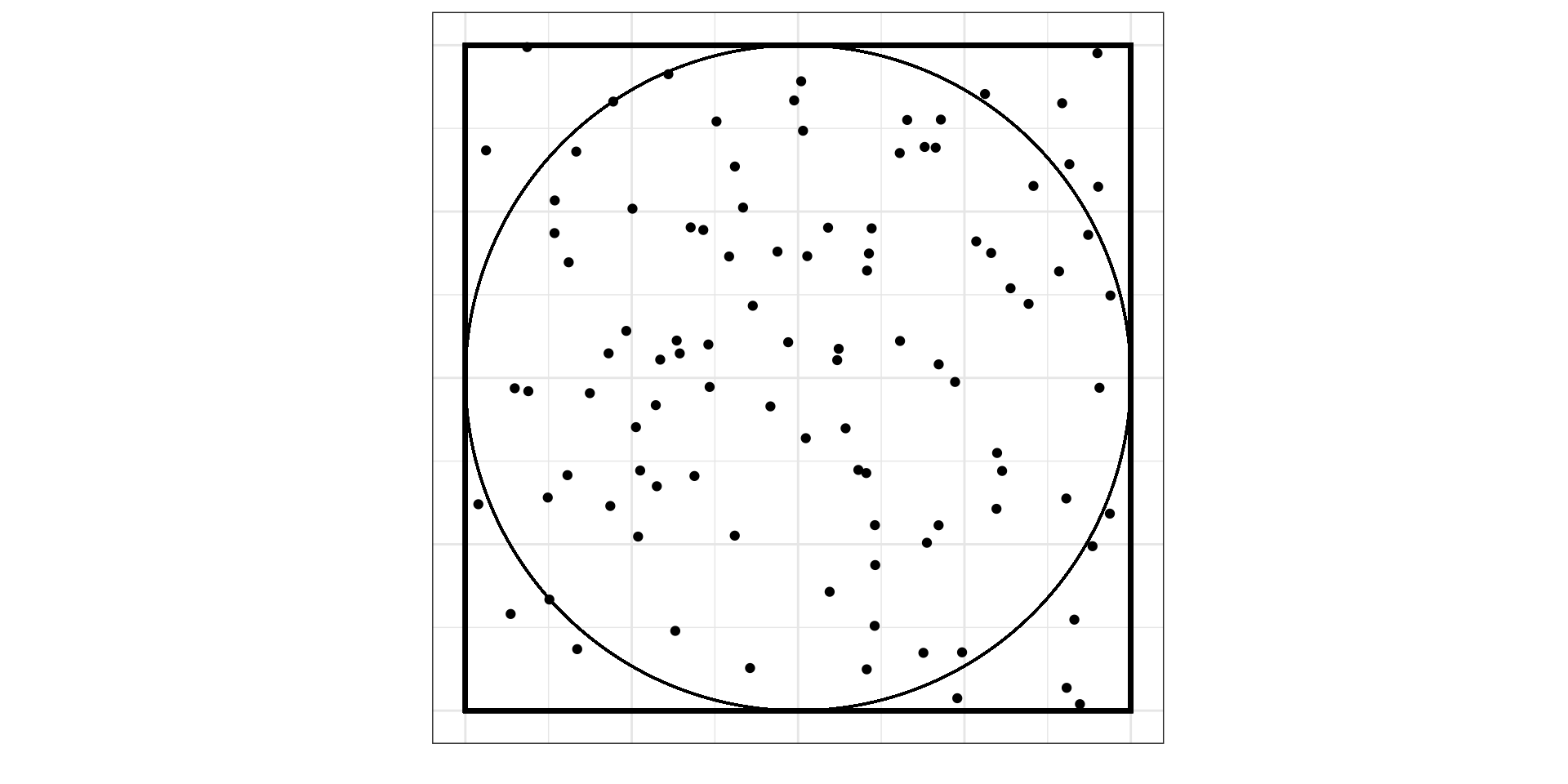
Какова вероятность, что случайно брошенная точка попадет в круг (событие \(A\))?

для \(\mathbb{R}^2\)

\[ \mathbb{P}(A) = \lim_{N \rightarrow \infty} \frac{n}{N} = \frac{S_\text{circle}}{S_\text{square}} \]

\[ \mathbb{P}(A) = \frac{S_\text{circle}}{S_\text{square}} = \frac{\pi r^2}{a^2} = \frac{\pi \big(\frac{1}{2}a\big)^2}{a^2} = \frac{1}{4}\pi \approx 0.785 \]

для \(\mathbb{R}^3\)

\[ \mathbb{P}(A) = \frac{V_\text{ball}}{V_\text{cube}} = \frac{\frac{4}{3}\pi r^3}{a^3} = \frac{\frac{4}{3}\pi \big(\frac{1}{2}a\big)^3}{a^3} \approx 0.523 \]

для \(\mathbb{R}^k\)

\[ \begin{split} k = 2n &, V = \frac{\pi^2}{n!}r^{2n} \\ k = 2n+1 &, V = \frac{2 \cdot (2\pi)^n}{(2n+1)!!} r^{2n+1} \end{split} \]

\(k \to \infty : V \to 0\).

Проклятие размерности

увеличивая количество переменных, мы делаем расстояния между точками больше
объем выборки должен расти экспоненциально, чтобы сохранялась достаточная точность оценки параметров

Что делать? Снижать размерность.

Задачи факторного анализа и анализа главных компонент

Сокращение числа переменных
Измерение неизмеримого (построение новых обобщеных показателей)
Наглядное представление многомерных наблюдений
Описание структуры взаимных связей между переменными
Преодоление мультиколлинеарности (в регрессионном анализе)
Заполнение пропущенных значений (при работе с разряженными матрицами)

и т.д.

Анализ главных компонент (Principal Component Analysis)

Математическая модель анализа главных компонент

Случайный вектор (матрица) \((\mathbf{X}_1, \mathbf{X}_2, \dots, \mathbf{X}_k)\)
- \(\mathbf{X}_i\) — некоторый столбец [числовых] данных
Задача — найти линейную комбинацию переменных, у которой максимальная дисперсия

\[ \begin{split} &\mathbf{Y}_1 = a_{11} \mathbf{X}_1 + a_{12} \mathbf{X}_2 + \dots + a_{1k} \mathbf{X}_k \\ &\text{var}(\mathbf{Y}_1) \to \max \\ &\mathbf{a}_1 \mathbf{a}_1^\top = 1, \, \mathbf{a}_1 = \begin{pmatrix} a_{11} & a_{12} \dots a_{1k} \end{pmatrix} \end{split} \]

\[ \begin{split} &\mathbf{Y}_2 = a_{21} \mathbf{X}_1 + a_{22} \mathbf{X}_2 + \dots + a_{2k} \mathbf{X}_k \\ &\text{var}(\mathbf{Y}_2) \to \max \\ &\mathbf{a}_2 \mathbf{a}_2^\top = 1, \, \mathbf{a}_2 = \begin{pmatrix} a_{21} & a_{22} \dots a_{2k} \end{pmatrix} \\ &\text{cor}(\mathbf{Y}_2, \mathbf{Y}_1) = 0 \end{split} \]

\[ \begin{split} &\mathbf{Y}_3 = a_{31} \mathbf{X}_1 + a_{32} \mathbf{X}_2 + \dots + a_{3k} \mathbf{X}_k \\ &\text{var}(\mathbf{Y}_3) \to \max \\ &\mathbf{a}_3 \mathbf{a}_3^\top = 1, \, \mathbf{a}_3 = \begin{pmatrix} a_{31} & a_{32} \dots a_{3k} \end{pmatrix} \\ &\text{cor}(\mathbf{Y}_3, \mathbf{Y}_1) = 0, \, \text{cor}(\mathbf{Y}_2, \mathbf{Y}_1) = 0 \end{split} \]

\[ \begin{split} &\mathbf{Y}_k = a_{k1} \mathbf{X}_1 + a_{k2} \mathbf{X}_2 + \dots + a_{kk} \mathbf{X}_k \\ &\text{var}(\mathbf{Y}_k) \to \max \\ &\mathbf{a}_k \mathbf{a}_k^\top = 1, \, \mathbf{a}_k = \begin{pmatrix} a_{k1} & a_{k2} \dots a_{kk} \end{pmatrix} \\ &\text{cor}(\mathbf{Y}_k, \mathbf{Y}_i) = 0, \, i = 1, 2, \ldots, k \end{split} \]

Главные компоненты

Полученные \(Y_i\) — искомые главные компоненты (principal components)
Новые оси, с помощью которых мы будем смотреть на данные и описывать их
Информативность — это дисперсия
Найти наиболее информативные линейные комбинации — некоторую «правильную систему координат».

Поиск главных компонент геометрически

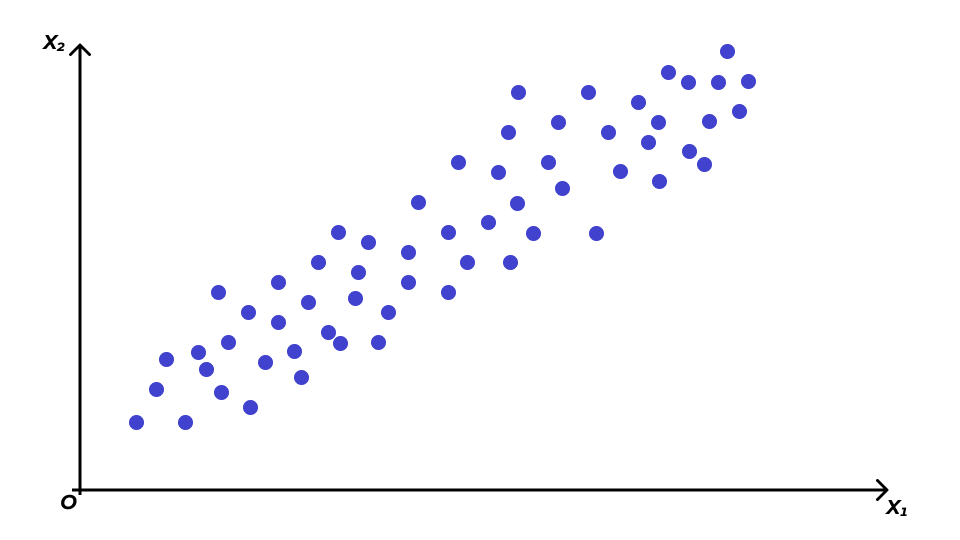
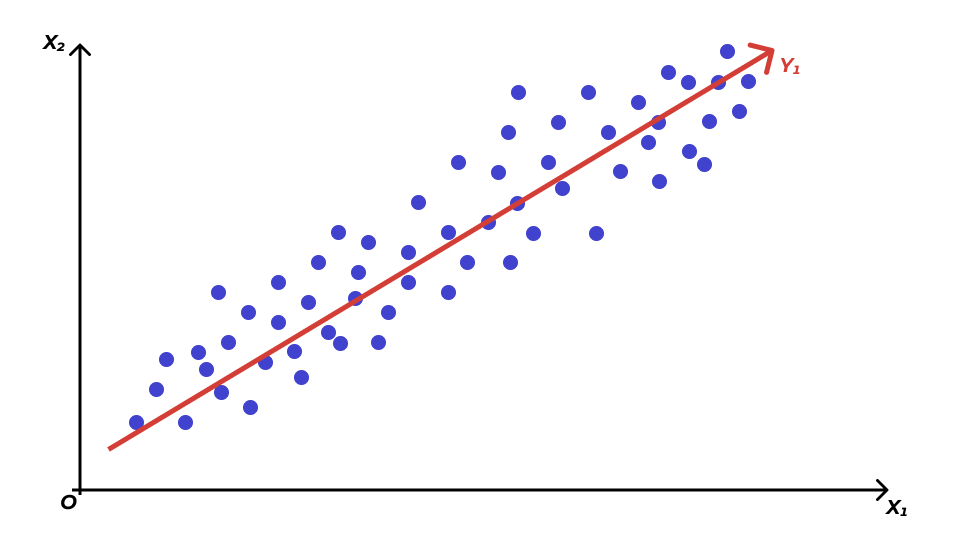
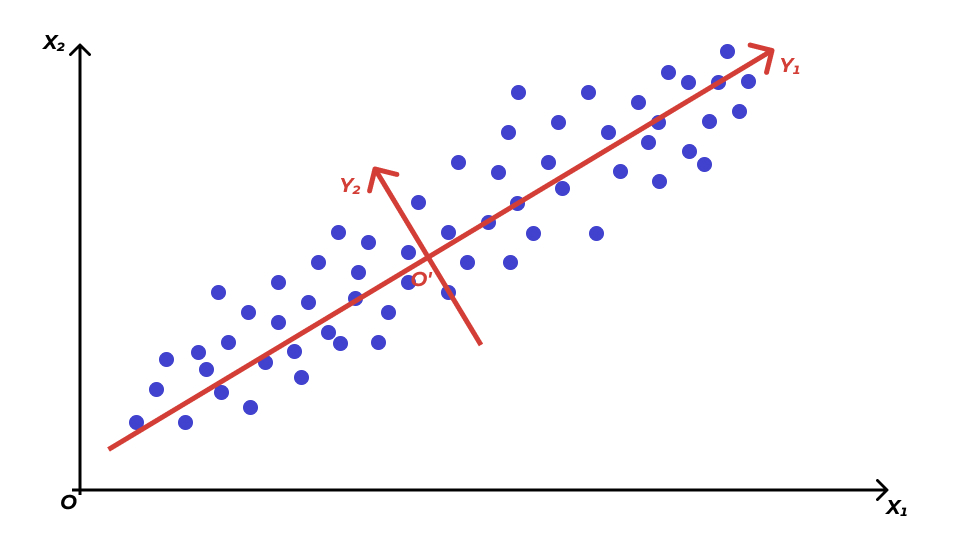
Сокращение размерности признакового пространства

Информативность компонент

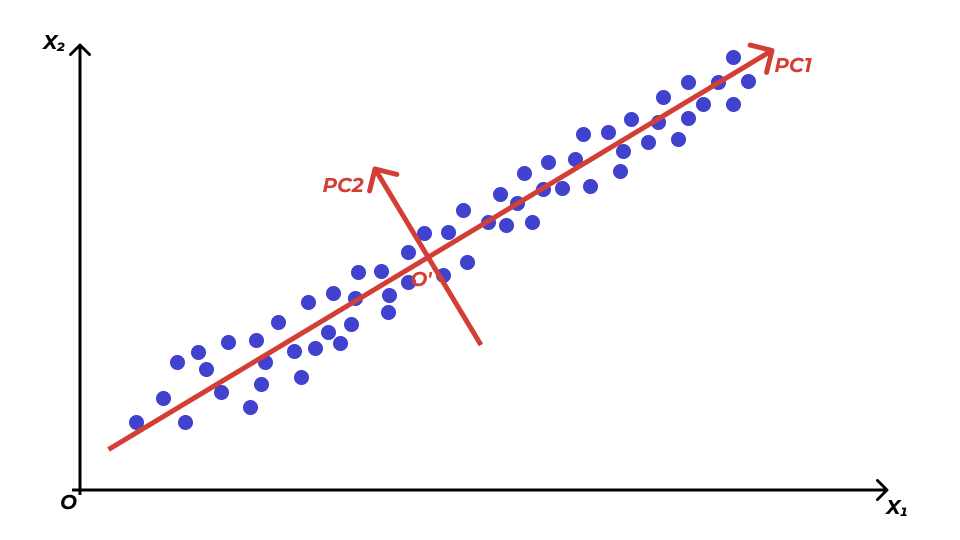
все наблюдения расположены более-менее вокруг одной прямой — первой главной компоненты \(\text{PC1}\)
изменчивостью по второй главной компоненте \(\text{PC2}\) можно пренебречь

Информативность компонент

каждая из главных компонент объясняет часть дисперсии данных
если новая переменная (главная компонента) объясняет меньше дисперсии, чем исходная переменная, то она не информативна
кумулятивная доля объясняемой дисперсии позволяет определить количество главных компонент, достаточное для объяснения не менее 80% дисперсии данных

	PC1	PC2	PC3	…	PCk
Standard Deviation	2.214	1.501	0.622	…	0.003
Proportion of Variance	0.596	0.327	0.059	…	0.000
Cumulative Proportion	0.596	0.923	0.982	…	1.000

Интерпретация главных компонент

матрица нагрузок (matrix of variable loadings)

	PC1	PC2	PC3	…	PCk
X1	0.06	−0.62	0.42	…	−0.42
X2	0.38	−0.27	−0.74	…	−0.27
X3	0.44	−0.24	0.19	…	−0.38
…	…	…	…	…	−0.05
Xk	0.24	0.57	−0.11	…	−0.77

Эксплораторный факторный анализ (Exploratory Factor Analysis)

Математическая модель эксплораторного факторного анализа

матрица наблюдений \(X^\top = \pmatrix{X_1 & X_2 & \ldots X_k}\)
за нашими наблюдениями лежат \(p\) факторов, \(p < k\)
матрица факторов \(F^\top = \pmatrix{F_1 & F_2 & \ldots & F_p}\)

\[ \begin{split} &\mathbf{X}_i = a_{i1} \mathbf{F}_1 + a_{i2} \mathbf{F}_2 + \dots + a_{ip} \mathbf{F}_p + \mathbf{U}_i, \, i = 1, 2, \ldots, k \\ & \mathbf{X} = \mathbf{A} \mathbf{F} + \mathbf{U}, \\ & \mathbf{A} = (a_{ij}), \, i = 1,2,\ldots,k, \, j = 1,2,\dots,p \\ & \mathbf{U}^\top = \pmatrix{\mathbf{U}_1 & \mathbf{U}_2 & \dots & \mathbf{U}_k} \end{split} \]

\(\mathbf{U}\) — то, что не удалось объяснить факторами (остатки, уникальность, uniqueness).

Допущения эксплораторного факторного анализа

\(\mathbb{E}\mathbf{X} = 0\).
\(\text{cor}(\mathbf{F}_j, \mathbf{F}_t) = 0, \, \forall j \forall t, \, j \neq t, j = 1,2,\ldots,p, \, t = 1,2,\ldots,p\).
\(\text{var}(\mathbf{F}) = \mathbf{I}\).
\(\text{cor}(\mathbf{U}_i, \mathbf{U}_r) = 0, \, \text{cor}(\mathbf{U}_i, \mathbf{F}_j) = 0, \, \forall i \forall r \forall j, i \neq r, \, i = 1,2,\ldots,k, \, r = 1,2,\ldots,k, \, j = 1,2,\ldots,p\).

Элементы матрицы \(\mathbf{A}\) — факторные нагрузки (factor loadings).
Элементы вектора \(\mathbf{U}\) — уникальные факторы (specific variates).

Уникальности

\[ \text{var}\mathbf{X}_i = \sum_{j=1}^p a^2_{ij} + \text{var}\mathbf{U}_i \]

чем больше уникальность (uniqueness), тем хуже наши факторы объясняют переменную.

Вращение факторов (factor rotation)

varimax — находит наиболее «контрастное» решение, еще более «изолируя» друг от друга факторы
quartimax — минимизирует количество факторов, необходимых для объяснения каждой переменной
equamax — количество переменных, сильно нагружающих фактор, и количество факторов для объяснения переменных минимальны
promax — наклонное вращение, позволяющее коррелировать факторы
oblimin — косоугольное вращение, позволяющее коррелировать факторы

Итоги

модели PCA и EFA
главные компоненты и факторы
решение задачи факторного анализа
вращение факторов

L14 // Анализ главных компонент. Эксплораторный факторный анализ

Антон Ангельгардт