L3 // Математика для анализа данных
Что будет?
- Алгебра логики и теория множеств
- Производная и интеграл
- Матрицы и работа с ними в линале
L3.1 // Дискретная математика
Алгебра логики
Формальная логика — это наука об общих структурах правильного мышления в его языковой форме
Высказывание
- отражает определённую объективную связь между предметами
- истинно, если в нём содержится адекватное отражение этой связи
- ложно в ином случае
Атомарные высказывания
- элементарные высказывания, которые невозможно разделить на составляющие — более мелкие высказывания
- могут быть либо истинны, либо ложны
- могут быть обозначены пропозициональными переменными
Логические операции
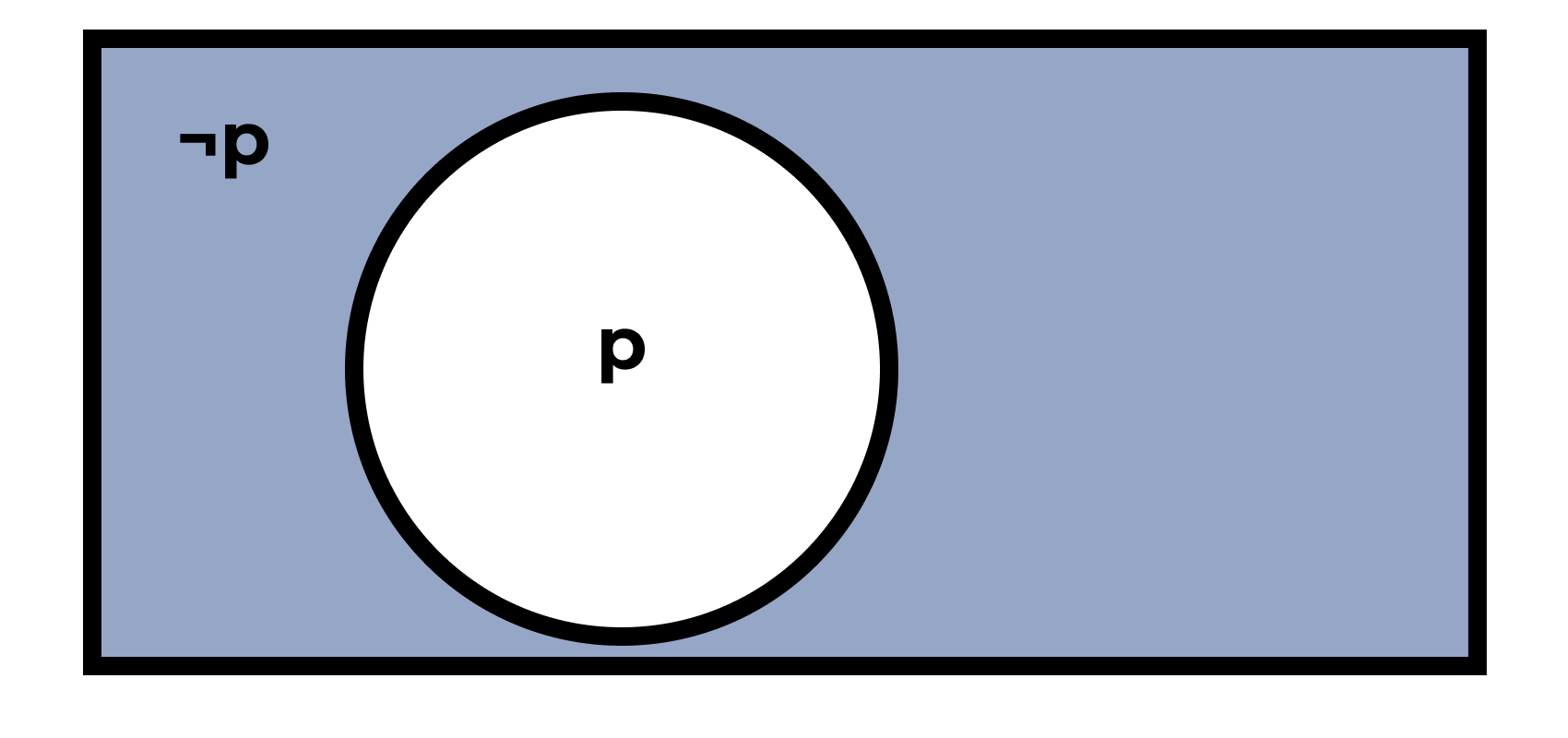
Инверсия, отрицание
| \(p\) | \(\neg p\) |
|---|---|
| истина | ложь |
| ложь | истина |
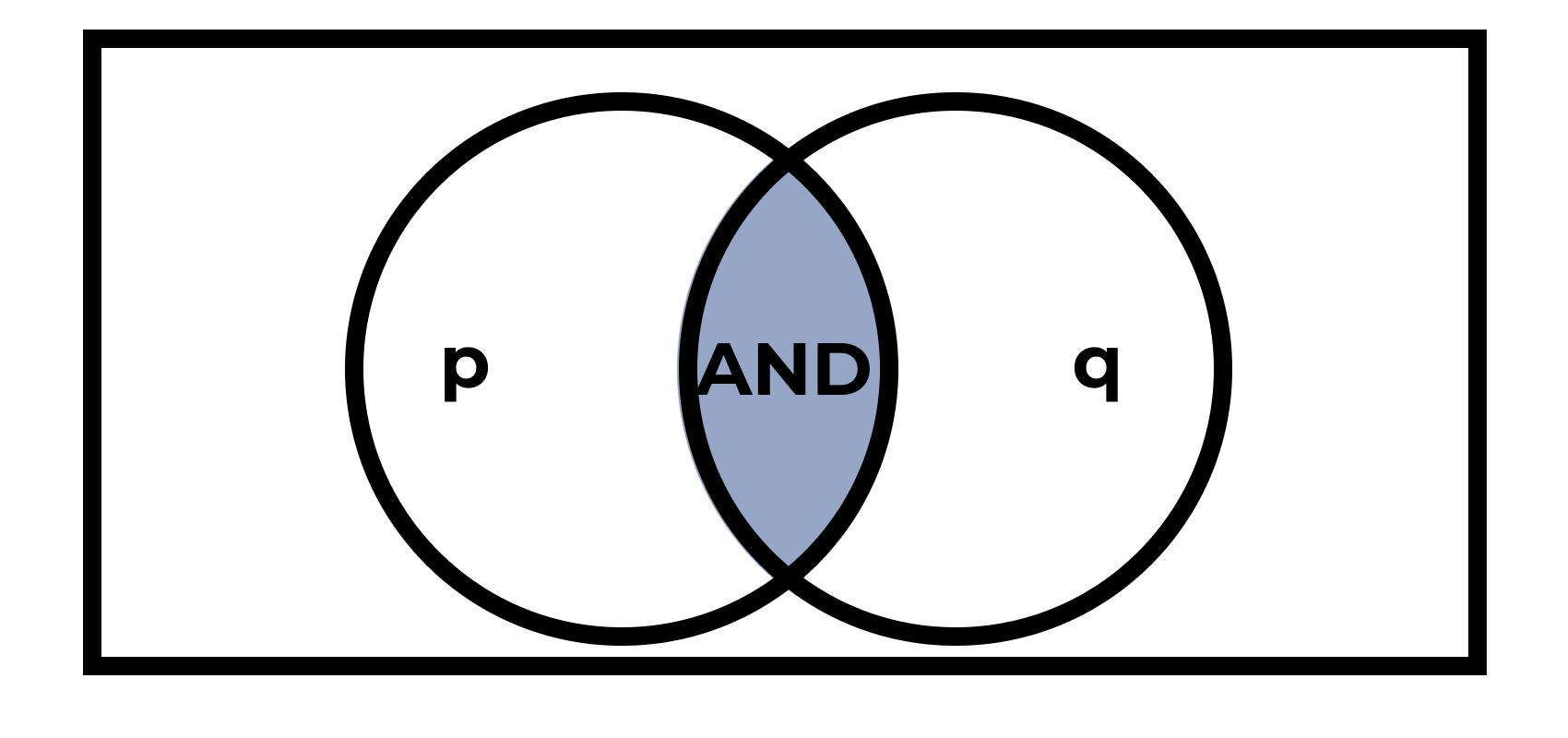
Конъюнкция, логическое умножение, логическое И
«как \(p\), так и \(q\)».
| \(p\) | \(q\) | \(p \wedge q\) |
|---|---|---|
| истина | истина | истина |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
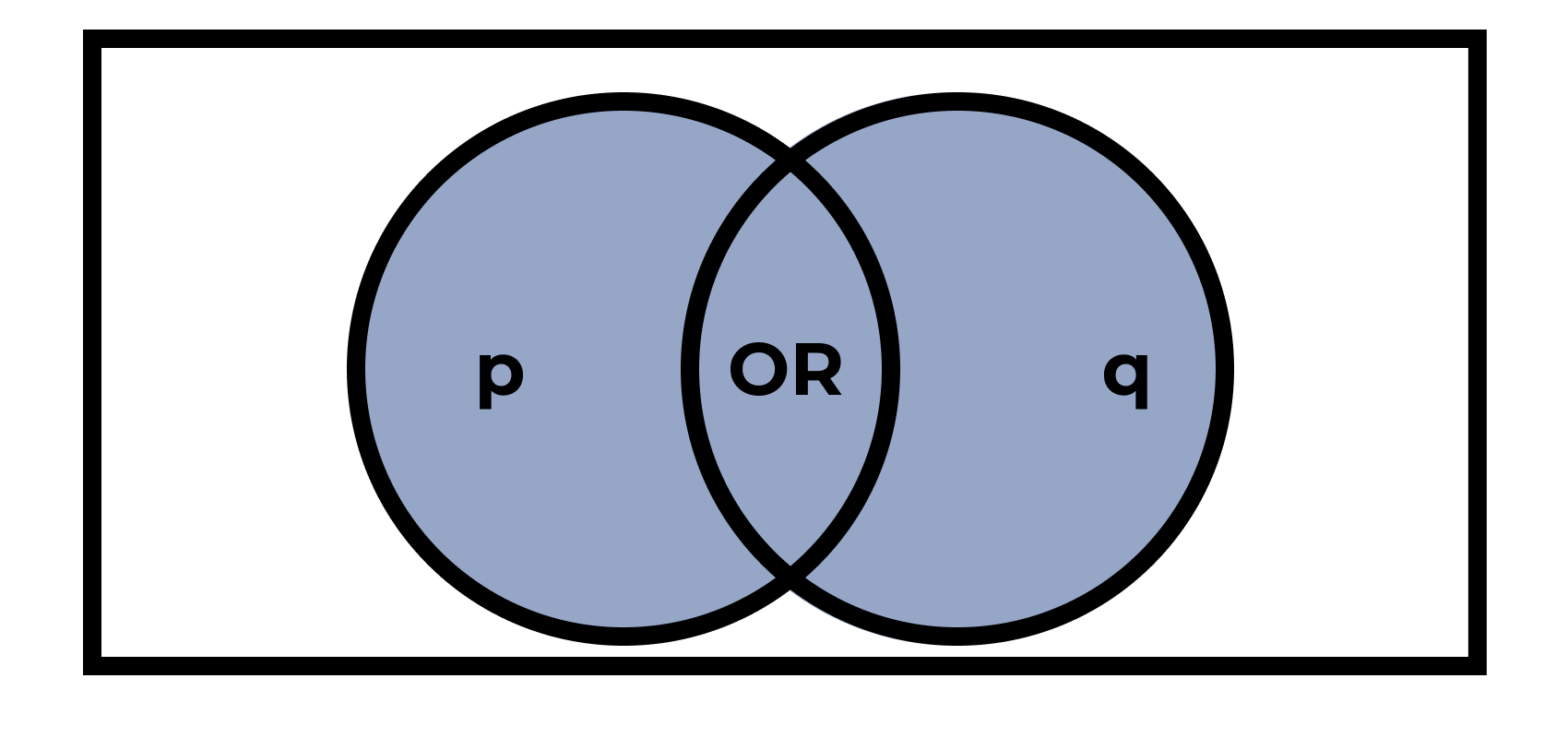
Дизъюнкция, логическое сложение, логические ИЛИ
«или \(p\), или \(q\), или и то и другое»
| \(p\) | \(q\) | \(p \vee q\) |
|---|---|---|
| истина | истина | истина |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
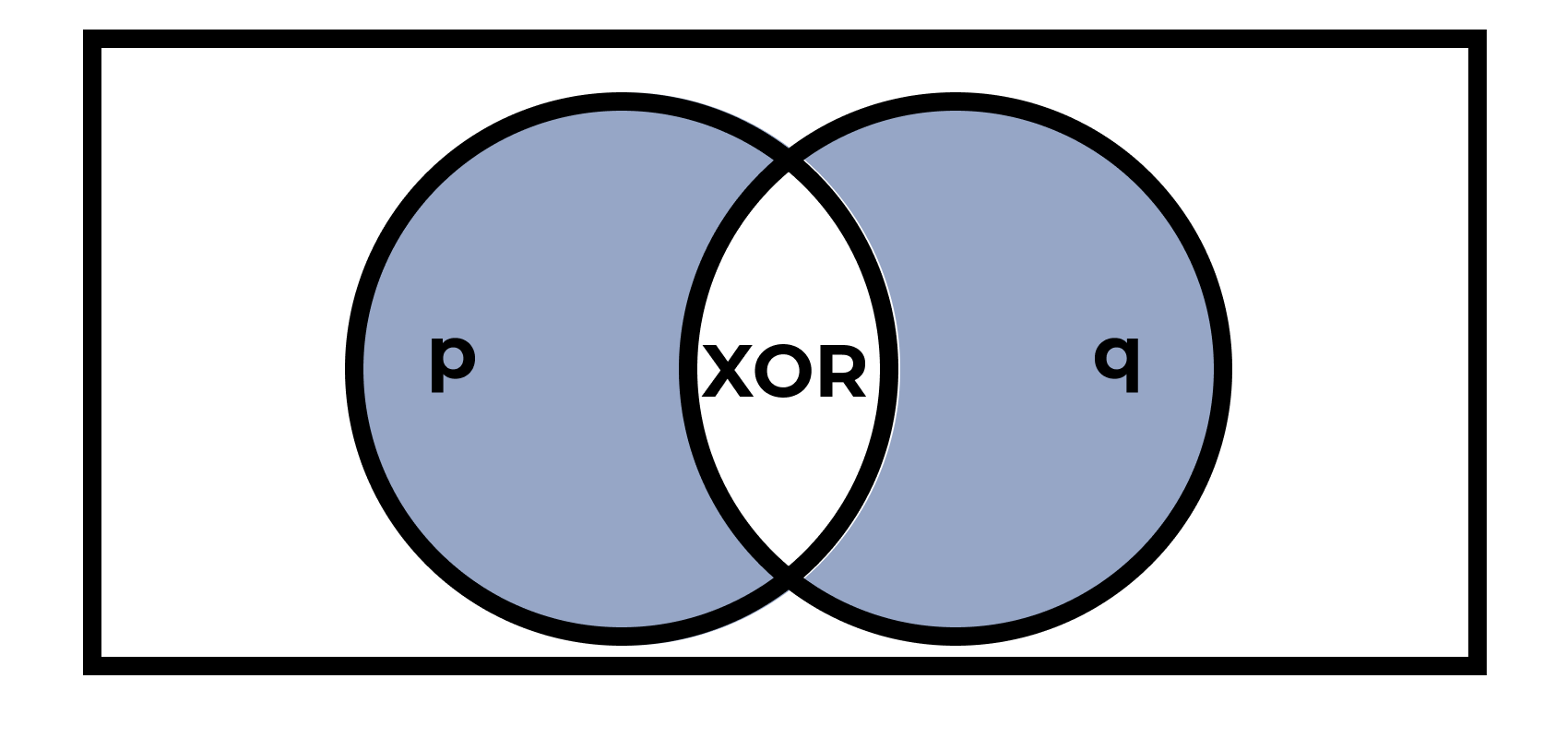
Разделительная дизъюнкция, исключающее ИЛИ
«либо \(p\), либо \(q\)»
| \(p\) | \(q\) | \(p \,\text{XOR}\,q\) |
|---|---|---|
| истина | истина | ложь |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
Условные высказывания
Импликация
«если \(p\), то \(q\)»
- \(p\) — антецедент
- \(q\) — консеквент
| \(p\) | \(q\) | \(p \rightarrow q\) |
|---|---|---|
| истина | истина | истина |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
Из ложного утверждения может следовать любое
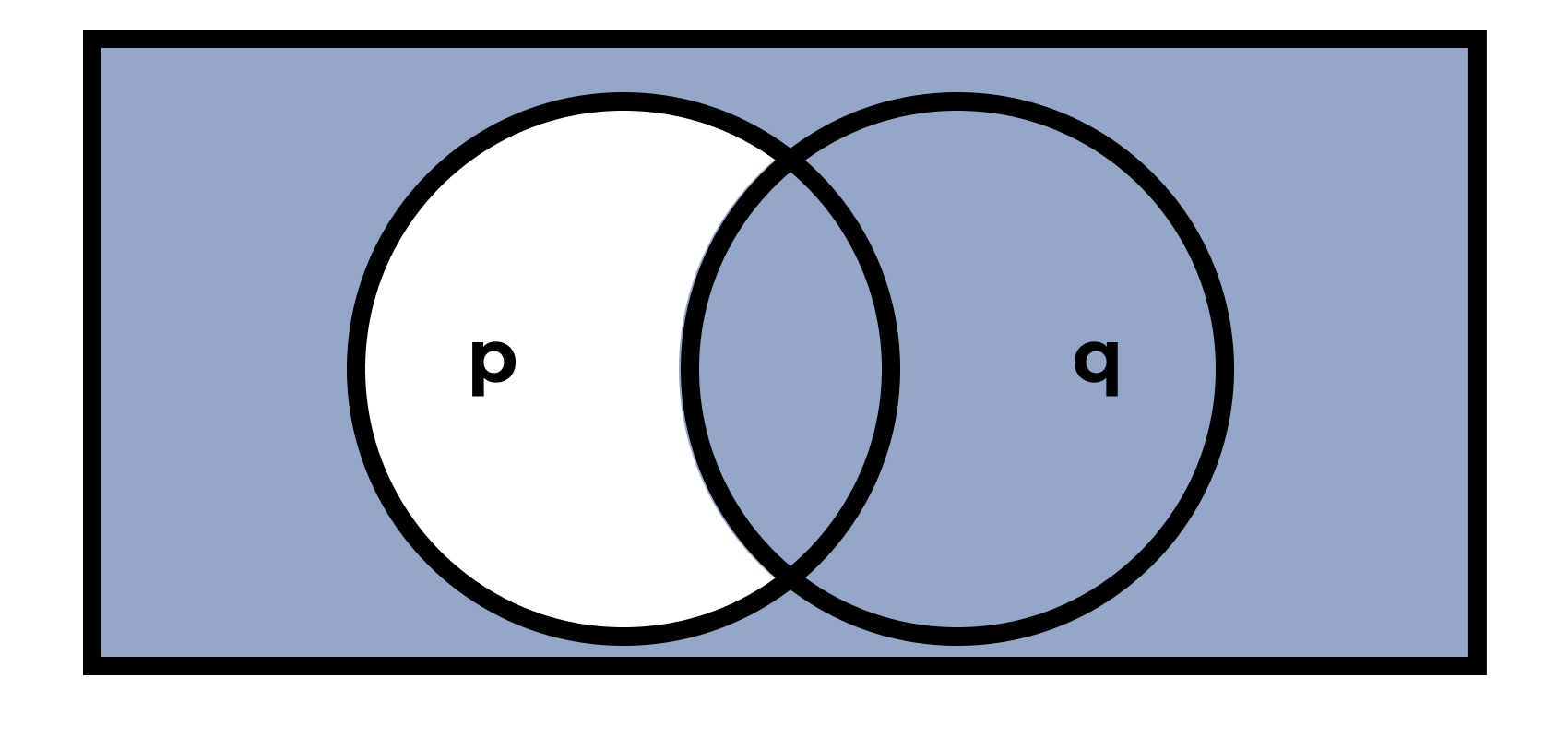
Репликация
«только если \(p\), то \(q\)»
| \(p\) | \(q\) | \(p \leftarrow q\) |
|---|---|---|
| истина | истина | истина |
| истина | ложь | истина |
| ложь | истина | ложь |
| ложь | ложь | истина |
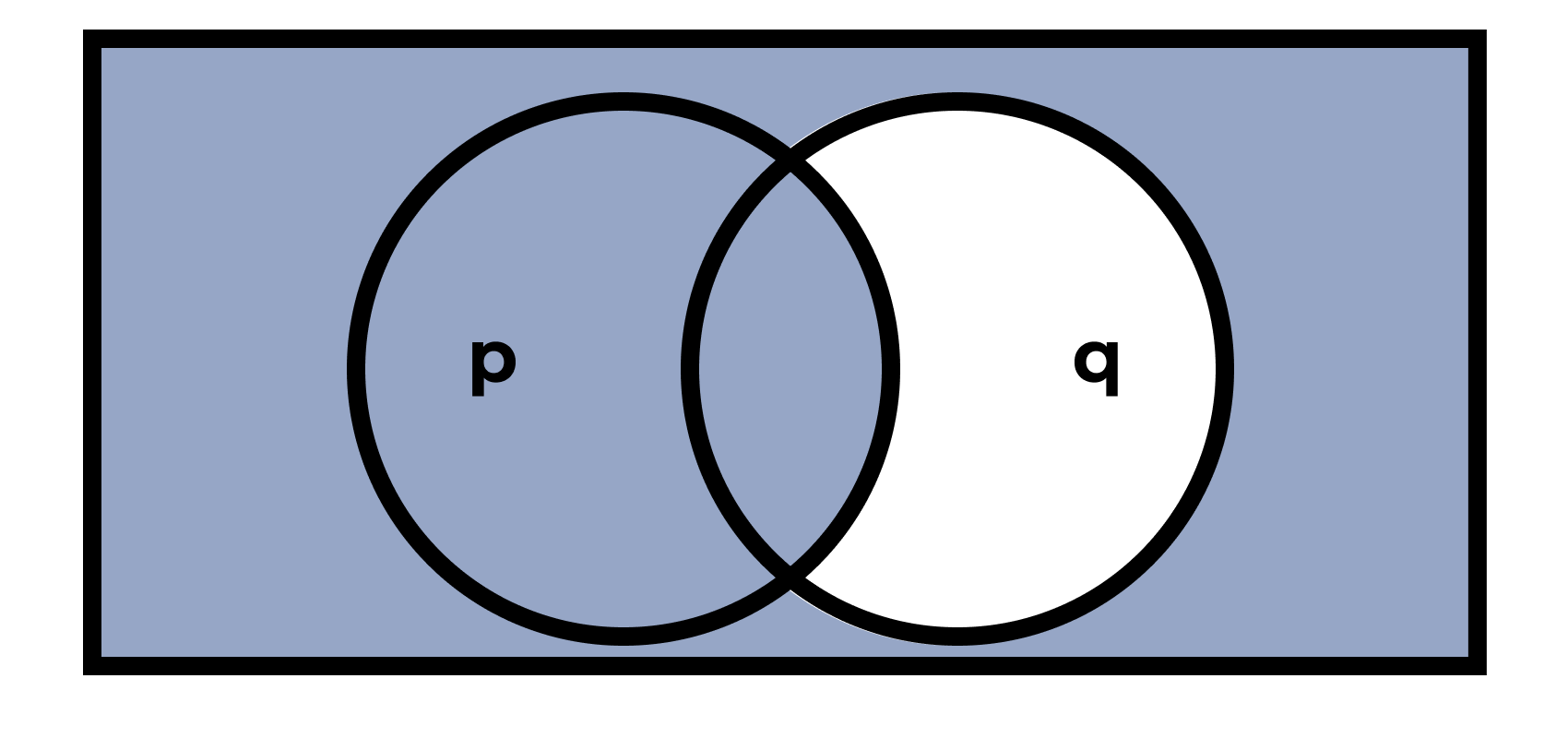
Эквиваленция
«\(p\) только тогда, когда \(q\)»
| \(p\) | \(q\) | \(p \leftrightarrow q\) |
|---|---|---|
| истина | истина | истина |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
Элементы теории множеств
Множество
- совокупность, или набор, некоторых (в общем случае любых) объектов
- обозначаются заглавными латинскими буквами (например, \(A\)), а его элементы — строчными латинскими буквами (например, \(a_1\), \(a_2\) и т.д.).
Множества удобно изображать кружочками. Примерно так:
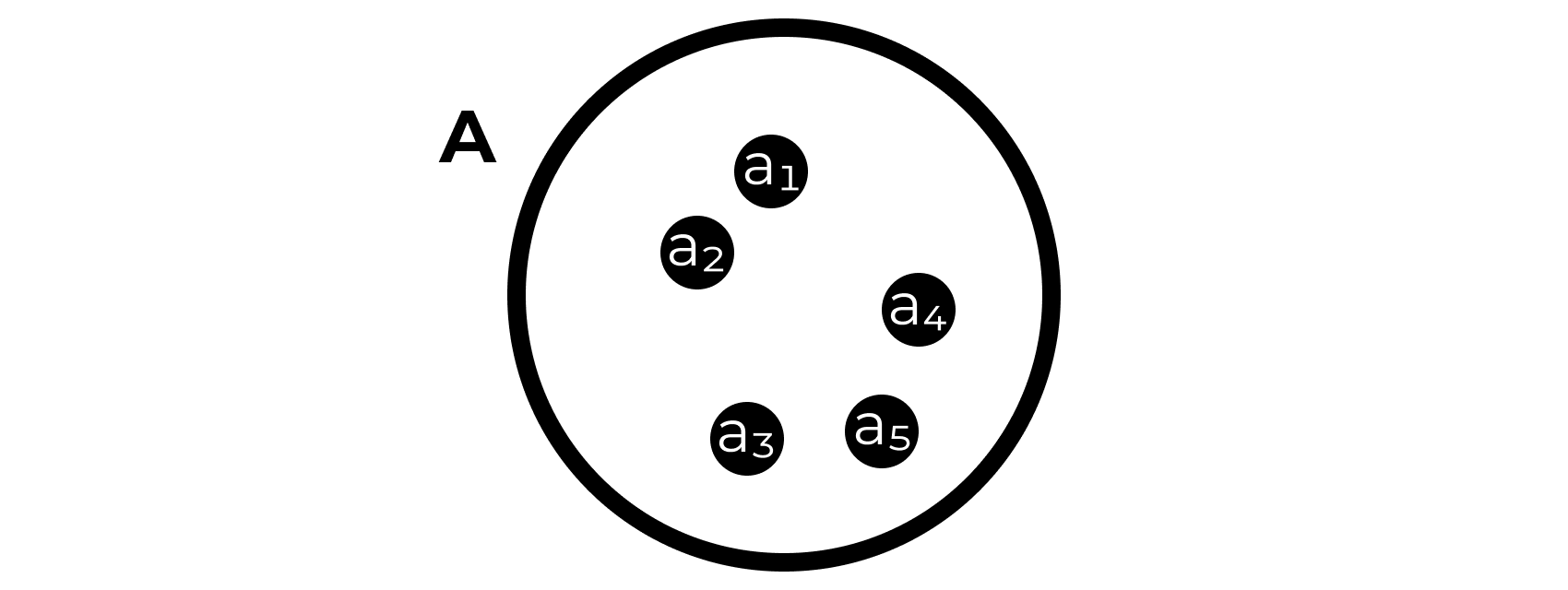
Множество
- Элемент может принадлежать данному множеству:
\[ a_i \in A \]
- Задать множество можно через перечисление элементов:
\[ B = \{ 0,1,2,3,4,5 \} \]
- Примеры множеств:
- Множество букв русского алфавита: \(L = \{ а, б, в, г, д, \dots, э, ю, я \}\)
- Множество всех натуральных чисел: \(\mathbb{N}= \{ 0, 1, 2, 3, \dots \}\)
- Множество всех целых чисел: \(\mathbb{Z}= \{0, 1, -1, 2, -2, 3, -3, \dots \}\)
Подмножество
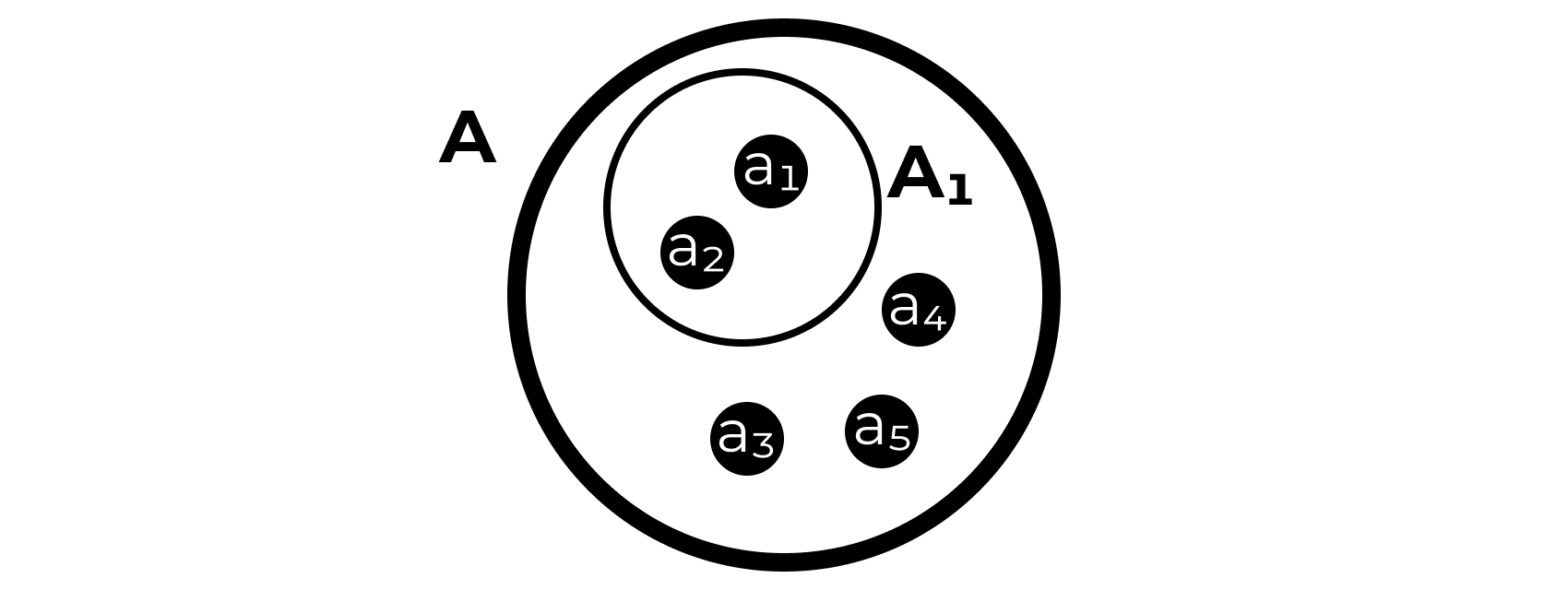
Множество \(A_1 = \{a_1, a_2\}\) является подмножеством множества \(A\):
\[ A_1 \subset A \]
- Множество натуральных чисел включается во множество целых \(\mathbb{N}\subset \mathbb{Z}\), и далее:
\[ \mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C} \]
- Тривиальными подмножествами любого множества являются пустое множество \(\varnothing\) и само это множество
\[ \varnothing \subset M \]
\[ M \subset M \]
Операции над множествами
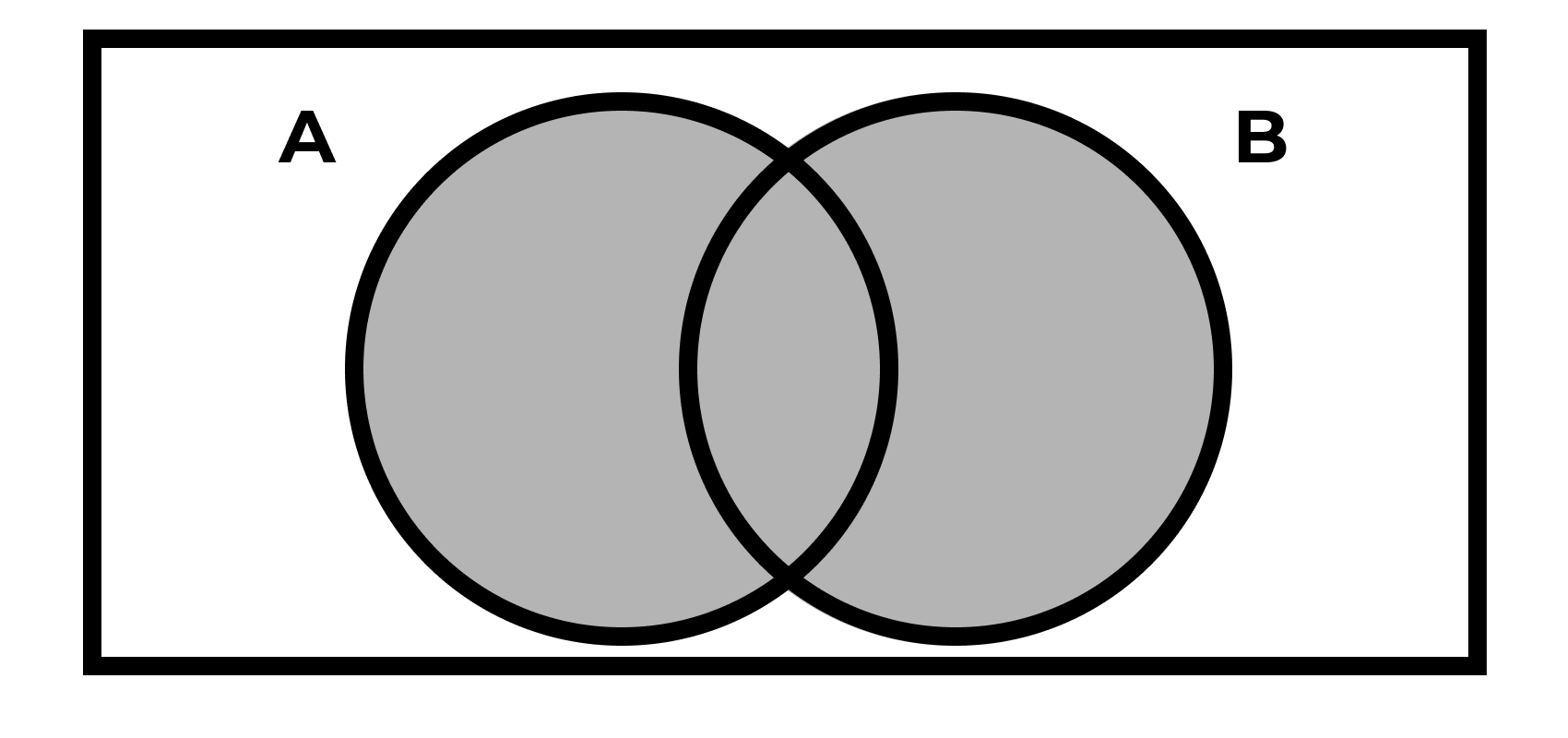
Объединение
\[ A + B = A \cup B = \{ x : x \in A \vee x \in B \} \]
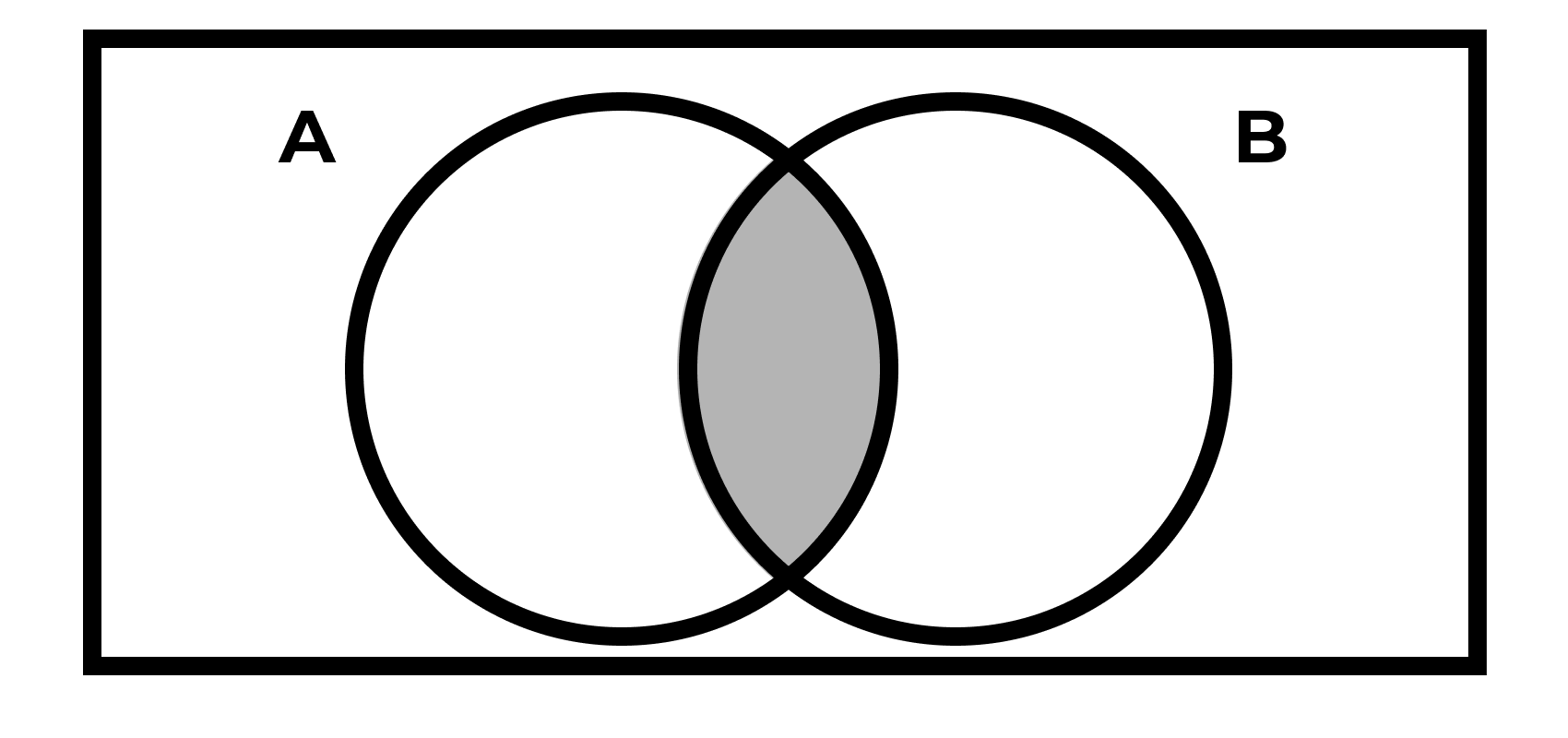
Пересечение
\[ A \cdot B = A \cap B = \{ x : x \in A \wedge x \in B \} \]
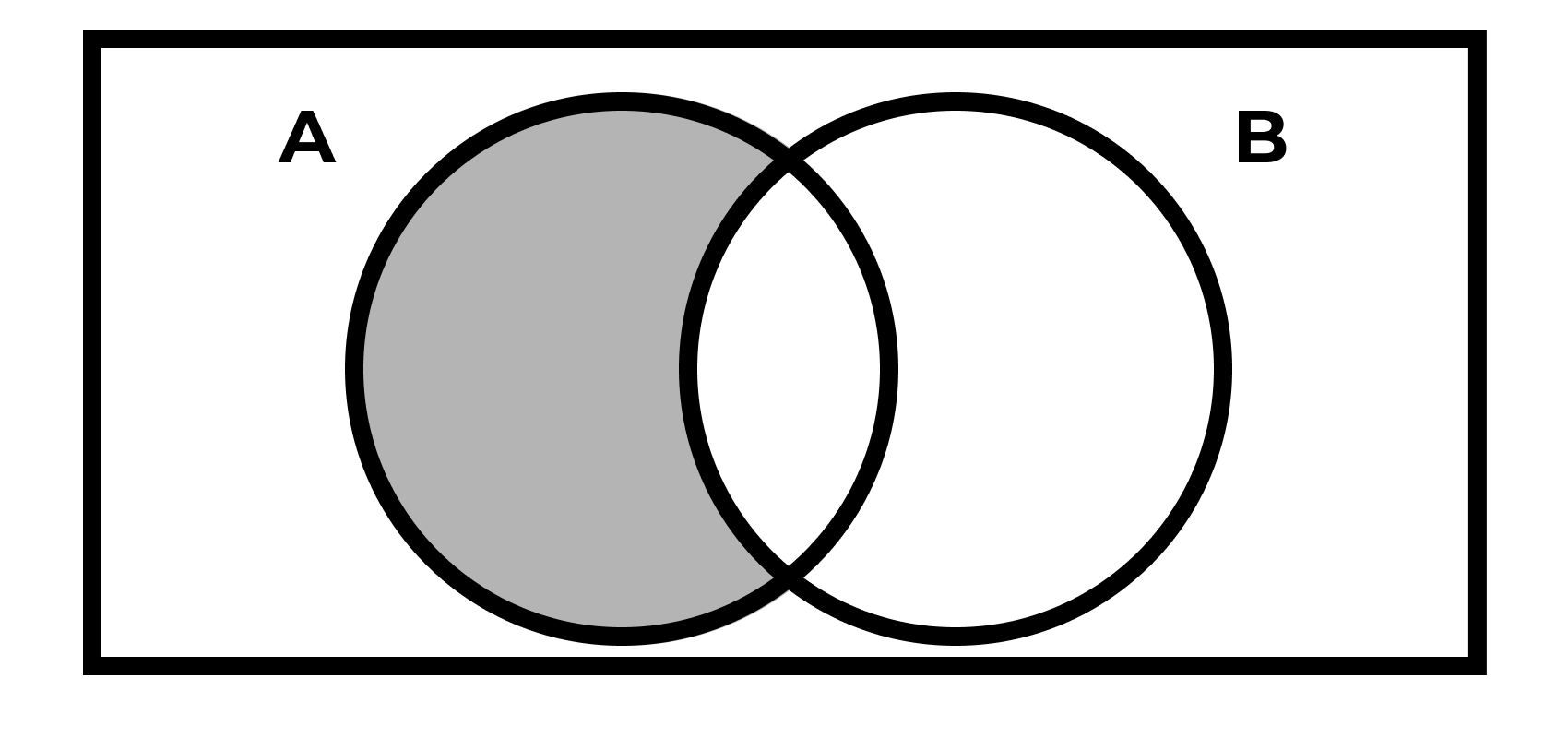
Разность множеств
\[ A ∖ B = \{ x : x \in A \wedge x \notin B \} \]
Дополнение
\[ U ∖ A = A^c = \bar A = \{ x : x \notin A \} \]
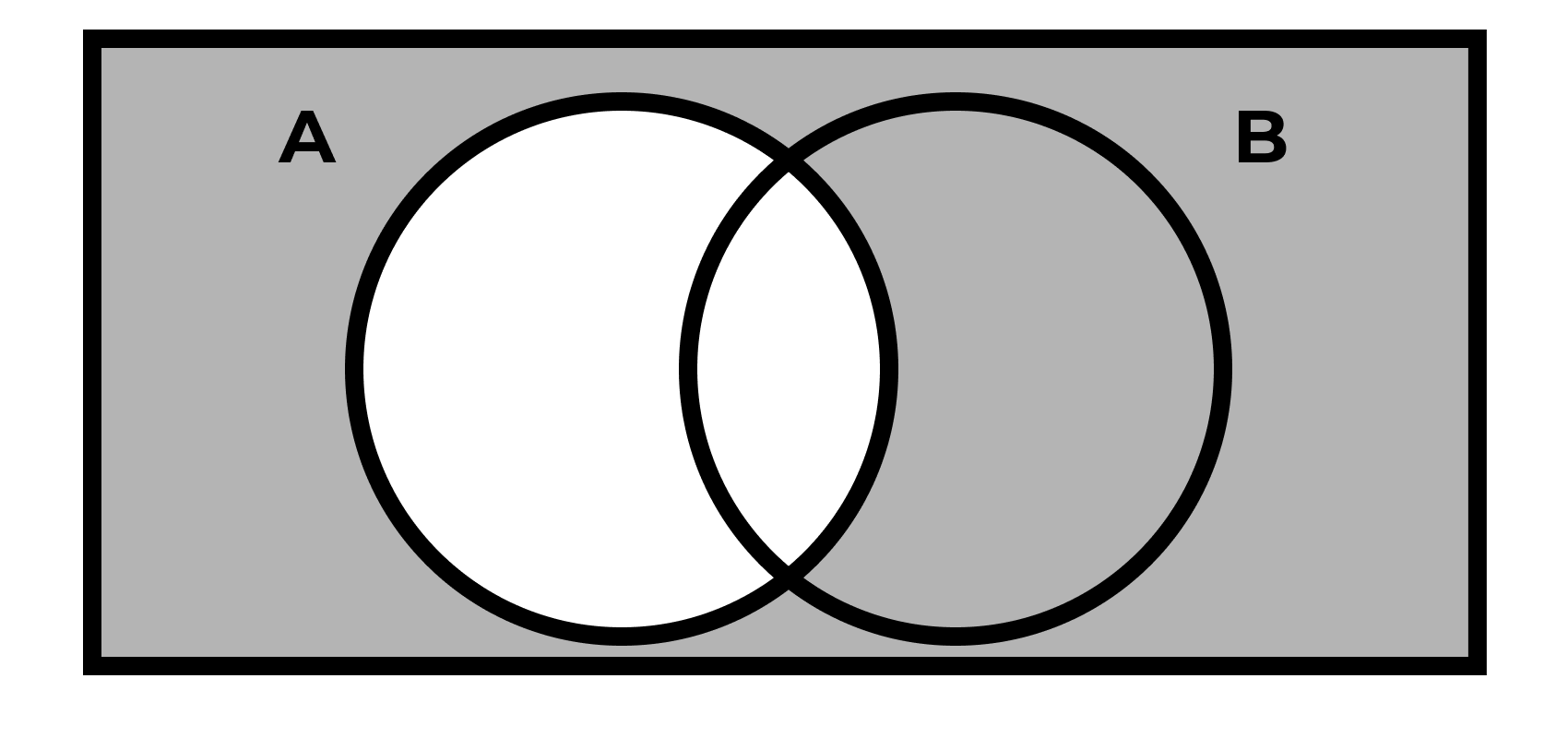
Симметрическая разность
\[ A \, \Delta \, B = ( A ∖ B ) \cup ( B ∖ A ) = \{ x : x \in A \,\text{XOR}\,x \in B \} \]
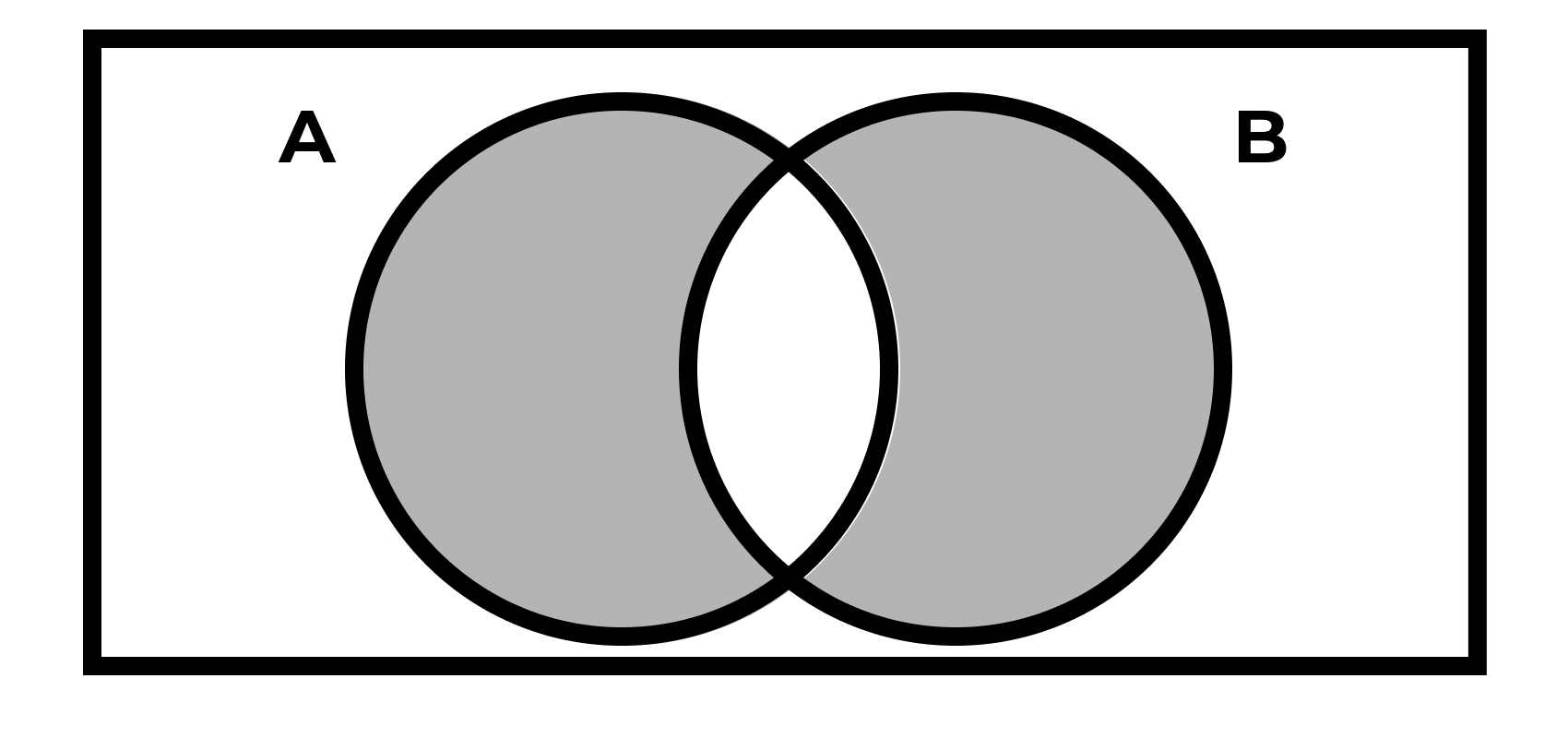
Декартово произведение
\[ A \times B = \{ (a,b) : a \in A, b \in B \} \]
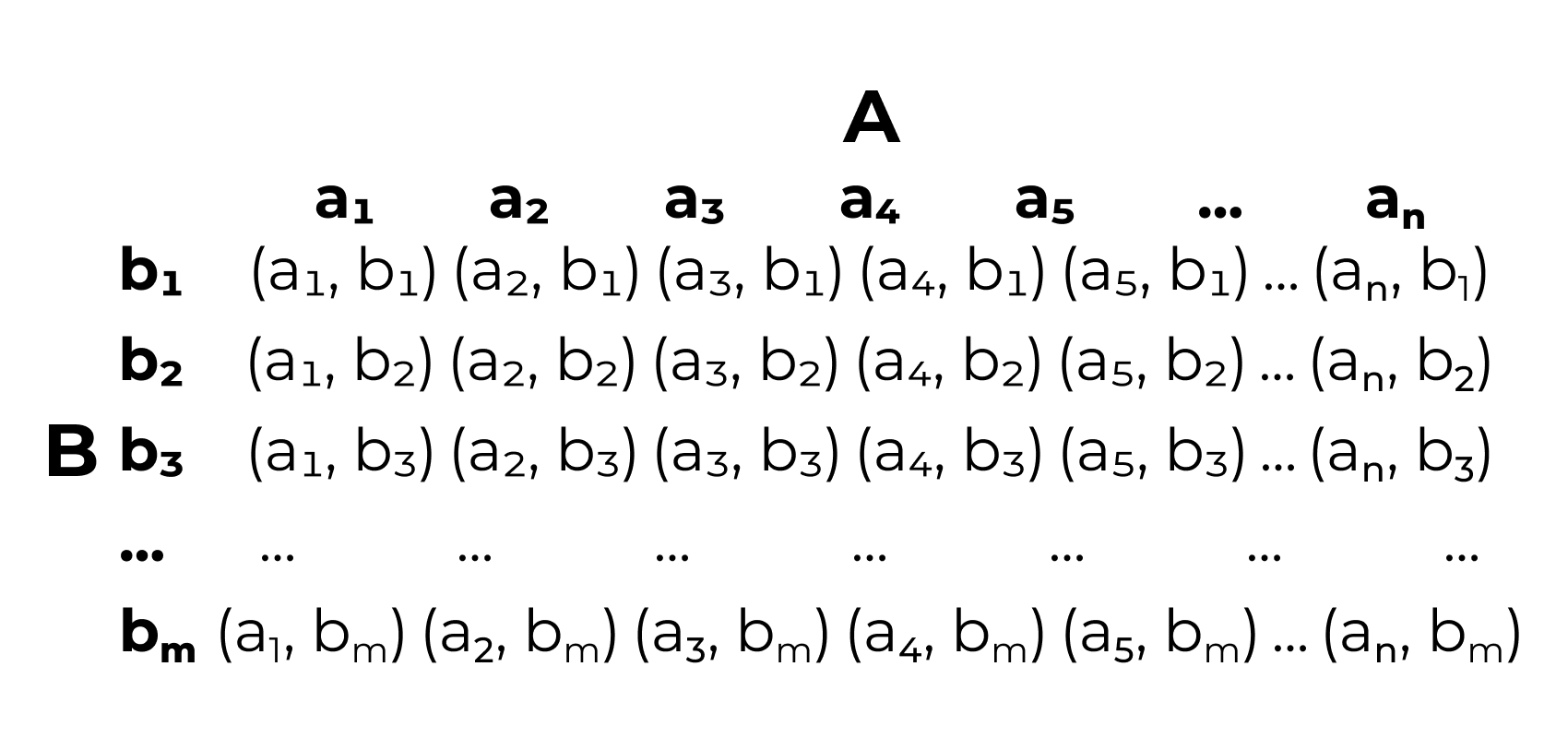
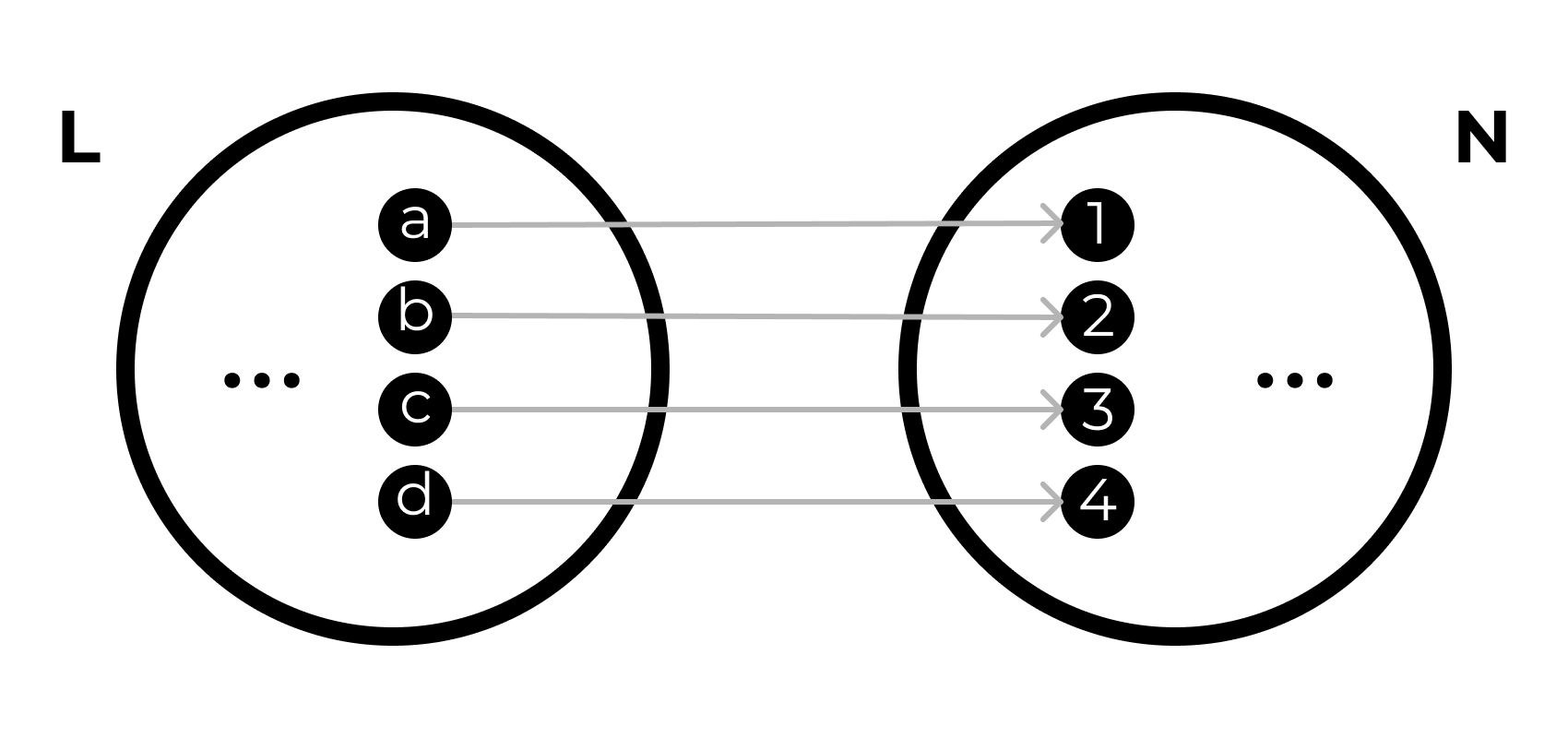
Отображения
- сопоставляет элементы одного множества элементам другого.
Пусть \(L\) — множество букв латинского алфавита
\[ L = \{ \text{a}, \text{b}, \text{c}, \text{d},\dots, \text{x}, \text{y}, \text{z} \} \]
а \(N\) — множество натуральных чисел от 1 до 26
\[ N = \{ 1,2,3, \dots,24,25,26 \} \]
Тогда мы можем задать такое отображение \(F\)
\[ F : L \rightarrow N, \]
где каждой букве будет соответствовать её порядковый номер в алфавите.
Мощность множества
- характеристика, описывающая, сколько элементов содержит данное множество
Множества могут быть конечными и бесконечными.
- Если множество конечно, то его мощность равна количеству его элементов.
- Например, множество очков, которое может выпаcть на стандартном игральном кубике — это \(S_1 = \{1,2,3,4,5,6\}\). Его мощность равна 6 — \(|S_1| = 6\).
- Множество значений пятибалльной шкалы Ликерта — это \(S_2 = \{1, 2, 3, 4, 5\}\). Его мощность равна 5 — \(|S_2| = 5\).
- Если множество бесконечно, то надо понять, насколько оно бесконечно.
Бесконечные множества
- Если можно построить отображение, в котором каждом элементу некоторого множества \(S\) будет сопоставлено единственное натуральное число, то такое множество называется счётным.
- Это значит, что элементов во множестве \(S\) бесконечное количество — так как количество натуральных чисел бесконечно — однако при неограниченном количестве времени их все-таки можно пересчитать.
- Мощность такого множетсва обозначается \(\aleph_0\), то есть \(|\mathbb{N}| = \aleph_0\).
- Если количество элементов множества больше количества натуральных чисел, то такое множество обладает мощностью континуума \(\aleph_1\).
- Это множество будет равномощно множеству вещественных чисел \(\mathbb{R}\).
Элементы комбинаторики
Перестановки
Формула числа перестановок из \(n\) элементов:
\[ P_n = n \cdot (n-1) \cdot (n-2) \cdot \ldots = n! \]
Любые \(n\) объектов можно расставить на \(n\) мест \(n!\) способами.
Например, для пяти элементов все возможные перестановки выглядят так:
\[ \matrix{ 1 & 2 & 3 & 4 & 5 \\ 1 & 2 & 3 & 5 & 4 \\ \\ 1 & 2 & 4 & 3 & 5 \\ 1 & 2 & 4 & 5 & 3 \\ \\ 1 & 2 & 5 & 3 & 4 \\ 1 & 2 & 5 & 4 & 3 \\ \\ \\ 1 & 3 & 2 & 4 & 5 \\ 1 & 3 & 2 & 5 & 4 \\ \\ 1 & 3 & 4 & 2 & 5 \\ 1 & 3 & 4 & 5 & 2 \\ \\ 1 & 3 & 5 & 2 & 4 \\ 1 & 3 & 5 & 4 & 2 \\ \\ \\ 1 & 4 & 2 & 3 & 5 \\ 1 & 4 & 2 & 5 & 3 \\ \\ 1 & 4 & 3 & 2 & 5 \\ 1 & 4 & 3 & 5 & 2 \\ \\ 1 & 4 & 5 & 2 & 3 \\ 1 & 4 & 5 & 3 & 2 \\ \\ \\ 1 & 5 & 2 & 3 & 4 \\ 1 & 5 & 2 & 4 & 3 \\ \\ 1 & 5 & 3 & 2 & 4 \\ 1 & 5 & 3 & 4 & 2 \\ \\ 1 & 5 & 4 & 2 & 3 \\ 1 & 5 & 4 & 3 & 2 \\ \\ \\ 2 & 1 & 3 & 4 & 5 \\ 2 & 1 & 3 & 5 & 4 \\ \\ 2 & 1 & 4 & 3 & 5 \\ 2 & 1 & 4 & 5 & 3 \\ \\ 2 & 1 & 5 & 3 & 4 \\ 2 & 1 & 5 & 4 & 3 \\ \\ \\ 2 & 3 & 1 & 4 & 5 \\ 2 & 3 & 1 & 5 & 4 \\ \\ 2 & 3 & 4 & 1 & 5 \\ 2 & 3 & 4 & 5 & 1 \\ \\ 2 & 3 & 5 & 1 & 4 \\ 2 & 3 & 5 & 4 & 1 \\ \\ \\ 2 & 4 & 1 & 3 & 5 \\ 2 & 4 & 1 & 5 & 3 \\ \\ 2 & 4 & 3 & 1 & 5 \\ 2 & 4 & 3 & 5 & 1 \\ \\ 2 & 4 & 5 & 1 & 3 \\ 2 & 4 & 5 & 3 & 1 \\ \\ \\ 2 & 5 & 1 & 3 & 4 \\ 2 & 5 & 1 & 4 & 3 \\ \\ 2 & 5 & 4 & 1 & 3 \\ 2 & 5 & 4 & 3 & 1 \\ \\ 2 & 5 & 3 & 1 & 4 \\ 2 & 5 & 3 & 4 & 1 \\ \\ \\ 3 & 1 & 2 & 4 & 5 \\ 3 & 1 & 2 & 5 & 4 \\ \\ 3 & 1 & 4 & 2 & 5 \\ 3 & 1 & 4 & 5 & 2 \\ \\ 3 & 1 & 5 & 2 & 4 \\ 3 & 1 & 5 & 4 & 2 \\ \\ \\ 3 & 2 & 1 & 4 & 5 \\ 3 & 2 & 1 & 5 & 4 \\ \\ 3 & 2 & 4 & 1 & 5 \\ 3 & 2 & 4 & 5 & 1 \\ \\ 3 & 2 & 5 & 1 & 4 \\ 3 & 2 & 5 & 4 & 1 \\ \\ \\ 3 & 4 & 1 & 2 & 5 \\ 3 & 4 & 1 & 5 & 2 \\ \\ 3 & 4 & 2 & 1 & 5 \\ 3 & 4 & 2 & 5 & 1 \\ \\ 3 & 4 & 5 & 1 & 2 \\ 3 & 4 & 5 & 2 & 1 \\ \\ \\ 3 & 5 & 1 & 2 & 4 \\ 3 & 5 & 1 & 4 & 2 \\ \\ 3 & 5 & 2 & 1 & 4 \\ 3 & 5 & 2 & 4 & 1 \\ \\ 3 & 5 & 4 & 1 & 2 \\ 3 & 5 & 4 & 2 & 1 \\ \\ \\ 4 & 1 & 2 & 3 & 5 \\ 4 & 1 & 2 & 5 & 3 \\ \\ 4 & 1 & 3 & 2 & 5 \\ 4 & 1 & 3 & 5 & 2 \\ \\ 4 & 1 & 5 & 2 & 3 \\ 4 & 1 & 5 & 3 & 2 \\ \\ \\ 4 & 2 & 1 & 3 & 5 \\ 4 & 2 & 1 & 5 & 3 \\ \\ 4 & 2 & 3 & 1 & 5 \\ 4 & 2 & 3 & 5 & 1 \\ \\ 4 & 2 & 5 & 1 & 3 \\ 4 & 2 & 5 & 3 & 1 \\ \\ \\ 4 & 3 & 1 & 2 & 5 \\ 4 & 3 & 1 & 5 & 2 \\ \\ 4 & 3 & 2 & 1 & 5 \\ 4 & 3 & 2 & 5 & 1 \\ \\ 4 & 3 & 5 & 1 & 2 \\ 4 & 3 & 5 & 2 & 1 \\ \\ \\ 4 & 5 & 1 & 2 & 3 \\ 4 & 5 & 1 & 3 & 2 \\ \\ 4 & 5 & 2 & 1 & 3 \\ 4 & 5 & 2 & 3 & 1 \\ \\ 4 & 5 & 3 & 1 & 2 \\ 4 & 5 & 3 & 2 & 1 \\ \\ \\ 5 & 1 & 2 & 3 & 4 \\ 5 & 1 & 2 & 4 & 3 \\ \\ 5 & 1 & 3 & 2 & 4 \\ 5 & 1 & 3 & 4 & 2 \\ \\ 5 & 1 & 4 & 2 & 3 \\ 5 & 1 & 4 & 3 & 2 \\ \\ \\ 5 & 2 & 1 & 3 & 4 \\ 5 & 2 & 1 & 4 & 3 \\ \\ 5 & 2 & 3 & 1 & 4 \\ 5 & 2 & 3 & 4 & 1 \\ \\ 5 & 2 & 4 & 1 & 3 \\ 5 & 2 & 4 & 3 & 1 \\ \\ \\ 5 & 3 & 1 & 2 & 4 \\ 5 & 3 & 1 & 4 & 2 \\ \\ 5 & 3 & 2 & 1 & 4 \\ 5 & 3 & 2 & 4 & 1 \\ \\ 5 & 3 & 4 & 1 & 2 \\ 5 & 3 & 4 & 2 & 1 \\ \\ \\ 5 & 4 & 1 & 2 & 3 \\ 5 & 4 & 1 & 3 & 2 \\ \\ 5 & 4 & 2 & 1 & 3 \\ 5 & 4 & 2 & 3 & 1 \\ \\ 5 & 4 & 3 & 1 & 2 \\ 5 & 4 & 3 & 2 & 1 \\ } \]
Размещения
Формула подсчета числа размещений (без повторений) из \(n\) элементов по \(k\) местам:
\[ A_n^k = \frac{n!}{(n-k)!} \]
Так как \(k < n\), то некоторые перестановки для нас становтся идентичны:
\[ \matrix{ 1 & 2 & 3 & [4 & 5] && 1 & 2 & 3 & [5 & 4] \\ \\ 1 & 2 & 4 & [3 & 5] && 1 & 2 & 4 & [5 & 3] \\ \\ 1 & 2 & 5 & [3 & 4] && 1 & 2 & 5 & [4 & 3] \\ \\ \\ 1 & 3 & 2 & [4 & 5] && 1 & 3 & 2 & [5 & 4] \\ \\ 1 & 3 & 4 & [2 & 5] && 1 & 3 & 4 & [5 & 2] \\ \\ 1 & 3 & 5 & [2 & 4] && 1 & 3 & 5 & [4 & 2] \\ \\ \\ 1 & 4 & 2 & [3 & 5] && 1 & 4 & 2 & [5 & 3] \\ \\ 1 & 4 & 3 & [2 & 5] && 1 & 4 & 3 & [5 & 2] \\ \\ 1 & 4 & 5 & [2 & 3] && 1 & 4 & 5 & [3 & 2] \\ \\ \\ 1 & 5 & 2 & [3 & 4] && 1 & 5 & 2 & [4 & 3] \\ \\ 1 & 5 & 3 & [2 & 4] && 1 & 5 & 3 & [4 & 2] \\ \\ 1 & 5 & 4 & [2 & 3] && 1 & 5 & 4 & [3 & 2] \\ \\ \\ 2 & 1 & 3 & [4 & 5] && 2 & 1 & 3 & [5 & 4] \\ \\ 2 & 1 & 4 & [3 & 5] && 2 & 1 & 4 & [5 & 3] \\ \\ 2 & 1 & 5 & [3 & 4] && 2 & 1 & 5 & [4 & 3] \\ \\ \\ 2 & 3 & 1 & [4 & 5] && 2 & 3 & 1 & [5 & 4] \\ \\ 2 & 3 & 4 & [1 & 5] && 2 & 3 & 4 & [5 & 1] \\ \\ 2 & 3 & 5 & [1 & 4] && 2 & 3 & 5 & [4 & 1] \\ \\ \\ 2 & 4 & 1 & [3 & 5] && 2 & 4 & 1 & [5 & 3] \\ \\ 2 & 4 & 3 & [1 & 5] && 2 & 4 & 3 & [5 & 1] \\ \\ 2 & 4 & 5 & [1 & 3] && 2 & 4 & 5 & [3 & 1] \\ \\ \\ 2 & 5 & 1 & [3 & 4] && 2 & 5 & 1 & [4 & 3] \\ \\ 2 & 5 & 4 & [1 & 3] && 2 & 5 & 4 & [3 & 1] \\ \\ 2 & 5 & 3 & [1 & 4] && 2 & 5 & 3 & [4 & 1] \\ \\ \\ 3 & 1 & 2 & [4 & 5] && 3 & 1 & 2 & [5 & 4] \\ \\ 3 & 1 & 4 & [2 & 5] && 3 & 1 & 4 & [5 & 2] \\ \\ 3 & 1 & 5 & [2 & 4] && 3 & 1 & 5 & [4 & 2] \\ \\ \\ 3 & 2 & 1 & [4 & 5] && 3 & 2 & 1 & [5 & 4] \\ \\ 3 & 2 & 4 & [1 & 5] && 3 & 2 & 4 & [5 & 1] \\ \\ 3 & 2 & 5 & [1 & 4] && 3 & 2 & 5 & [4 & 1] \\ \\ \\ 3 & 4 & 1 & [2 & 5] && 3 & 4 & 1 & [5 & 2] \\ \\ 3 & 4 & 2 & [1 & 5] && 3 & 4 & 2 & [5 & 1] \\ \\ 3 & 4 & 5 & [1 & 2] && 3 & 4 & 5 & [2 & 1] \\ \\ \\ 3 & 5 & 1 & [2 & 4] && 3 & 5 & 1 & [4 & 2] \\ \\ 3 & 5 & 2 & [1 & 4] && 3 & 5 & 2 & [4 & 1] \\ \\ 3 & 5 & 4 & [1 & 2] && 3 & 5 & 4 & [2 & 1] \\ \\ \\ 4 & 1 & 2 & [3 & 5] && 4 & 1 & 2 & [5 & 3] \\ \\ 4 & 1 & 3 & [2 & 5] && 4 & 1 & 3 & [5 & 2] \\ \\ 4 & 1 & 5 & [2 & 3] && 4 & 1 & 5 & [3 & 2] \\ \\ \\ 4 & 2 & 1 & [3 & 5] && 4 & 2 & 1 & [5 & 3] \\ \\ 4 & 2 & 3 & [1 & 5] && 4 & 2 & 3 & [5 & 1] \\ \\ 4 & 2 & 5 & [1 & 3] && 4 & 2 & 5 & [3 & 1] \\ \\ \\ 4 & 3 & 1 & [2 & 5] && 4 & 3 & 1 & [5 & 2] \\ \\ 4 & 3 & 2 & [1 & 5] && 4 & 3 & 2 & [5 & 1] \\ \\ 4 & 3 & 5 & [1 & 2] && 4 & 3 & 5 & [2 & 1] \\ \\ \\ 4 & 5 & 1 & [2 & 3] && 4 & 5 & 1 & [3 & 2] \\ \\ 4 & 5 & 2 & [1 & 3] && 4 & 5 & 2 & [3 & 1] \\ \\ 4 & 5 & 3 & [1 & 2] && 4 & 5 & 3 & [2 & 1] \\ \\ \\ 5 & 1 & 2 & [3 & 4] && 5 & 1 & 2 & [4 & 3] \\ \\ 5 & 1 & 3 & [2 & 4] && 5 & 1 & 3 & [4 & 2] \\ \\ 5 & 1 & 4 & [2 & 3] && 5 & 1 & 4 & [3 & 2] \\ \\ \\ 5 & 2 & 1 & [3 & 4] && 5 & 2 & 1 & [4 & 3] \\ \\ 5 & 2 & 3 & [1 & 4] && 5 & 2 & 3 & [4 & 1] \\ \\ 5 & 2 & 4 & [1 & 3] && 5 & 2 & 4 & [3 & 1] \\ \\ \\ 5 & 3 & 1 & [2 & 4] && 5 & 3 & 1 & [4 & 2] \\ \\ 5 & 3 & 2 & [1 & 4] && 5 & 3 & 2 & [4 & 1] \\ \\ 5 & 3 & 4 & [1 & 2] && 5 & 3 & 4 & [2 & 1] \\ \\ \\ 5 & 4 & 1 & [2 & 3] && 5 & 4 & 1 & [3 & 2] \\ \\ 5 & 4 & 2 & [1 & 3] && 5 & 4 & 2 & [3 & 1] \\ \\ 5 & 4 & 3 & [1 & 2] && 5 & 4 & 3 & [2 & 1] \\ } \]
Сочетания
Формула для подсчета числа сочетаний из \(n\) элементов по \(k\):
\[ С_n^k = \frac{n!}{k!(n-k)!} \]
Нам все равно на порядок элементов, поэтому число сочетаний меньше числа размещений в количество раз, равное числу перестановок \(k!\).
Все возможные сочетания пяти элементов по три представлены ниже:
\[ \matrix { 1 & 2 & 3 && 1 & 4 & 5 \\ 1 & 2 & 4 && 2 & 3 & 4 \\ 1 & 2 & 5 && 2 & 3 & 5 \\ 1 & 3 & 4 && 2 & 4 & 5 \\ 1 & 3 & 5 && 3 & 4 & 5 } \]
L3.2 // Элементы математического анализа
Последовательности
Числовая последовательность — это последовательность любых чисел.
\[ (x_n)^\infty_{n=1} \]
- \(x_n\) — это некоторый элемент последовательности
- верхний и нижний индексы обозначают границы изменения индекса \(n\).
Например, \(\langle 1,-1,1,-1,\dots \rangle\) — это числовая последовательность, которую можно обозначить \(\big( (-1)^n \big)^\infty_{n=1}\).
Монотонная последовательность
- это последовательность, которая
- не возрастает — то есть стоит на месте или убывает
- или не убывает — то есть стоит на месте или возрастает
Предел последовательности
Если существует такой объект (число), к которому элементы последовательности приближаются с ростом номера, то он является пределом этой последовательности.
Пусть есть последовательность:
\[ \Big( \frac{1}{n} \Big)^{\infty}_{n=1} = \Big \langle 1, \frac{1}{2}, \frac{1}{3}, \dots \Big \rangle \]
- каждый следующий её элемент, меньше предыдущего
- отрицательными элементы данной последовательности быть не могут
- когда-то последовательность упрётся в ноль.
Формальное определение предела последовательности
Число \(a\) называется пределом последовательности \(\{x_n\}\), если для любого положительного числа \(\varepsilon\) существует номер \(N_\varepsilon\), такой что для любого \(n > N_\varepsilon\), выполняется равенство \(|x_n - a| < \varepsilon\), или на математическом:
\[ \lim_{n \rightarrow \infty} x_n = a \Leftrightarrow \forall \varepsilon > 0 \, \, \exists N_\varepsilon \in \mathbb{N}: n \geq N_\varepsilon, |x_n - a| < \varepsilon \]
Функции
- Функция устанавливает соответствие между элементами двух числовых множеств.
- У любой функции есть область определения (множество \(X\)) и область значений (множество \(Y\)). Сама же функция представляет собой множество упорядоченных пар
\[ (x,y) \in X \times Y, \] таких что
- пары существуют для всех элементов \(X\), и
- если первые элементы пар равны, то равны и их вторые элементы.
Дискретная функция
Если функция определена на множестве целых чисел \(\mathbb{Z}\), то она будет дискретная, так как между, например, \(1\) и \(2\) будет пусто.
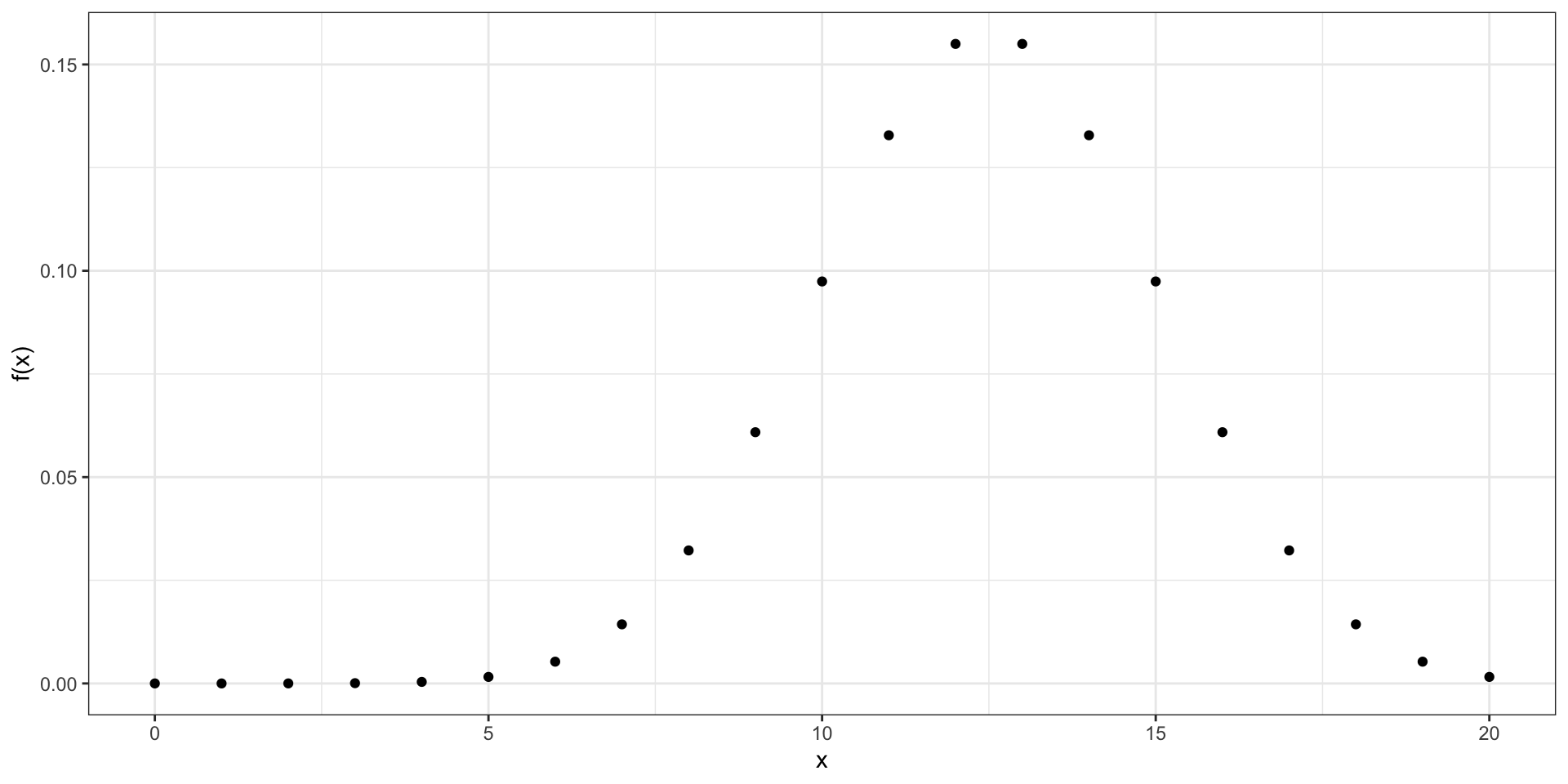
Непрерывная функция
Если функция определена на множестве \(\mathbb{R}\), то она будет непрерывной. Например, функция \(f(x) = x^2\) является непрерывной, как ифункции \(f(x) = \sqrt{x}\) и \(f(x) = \ln(x)\). Если функция непрерывная, то она дифференцируема.
Производная
А раз они дифференцируемы, то мы можем взять производную!
Производная показывает
- тангенс угла наклона касательной в данной точке
- скорость и направление изменения функции в данной точке
Логика производной
Пусть дана функция \(f(x) = 2x^3 + 3x^2-4x+6\).
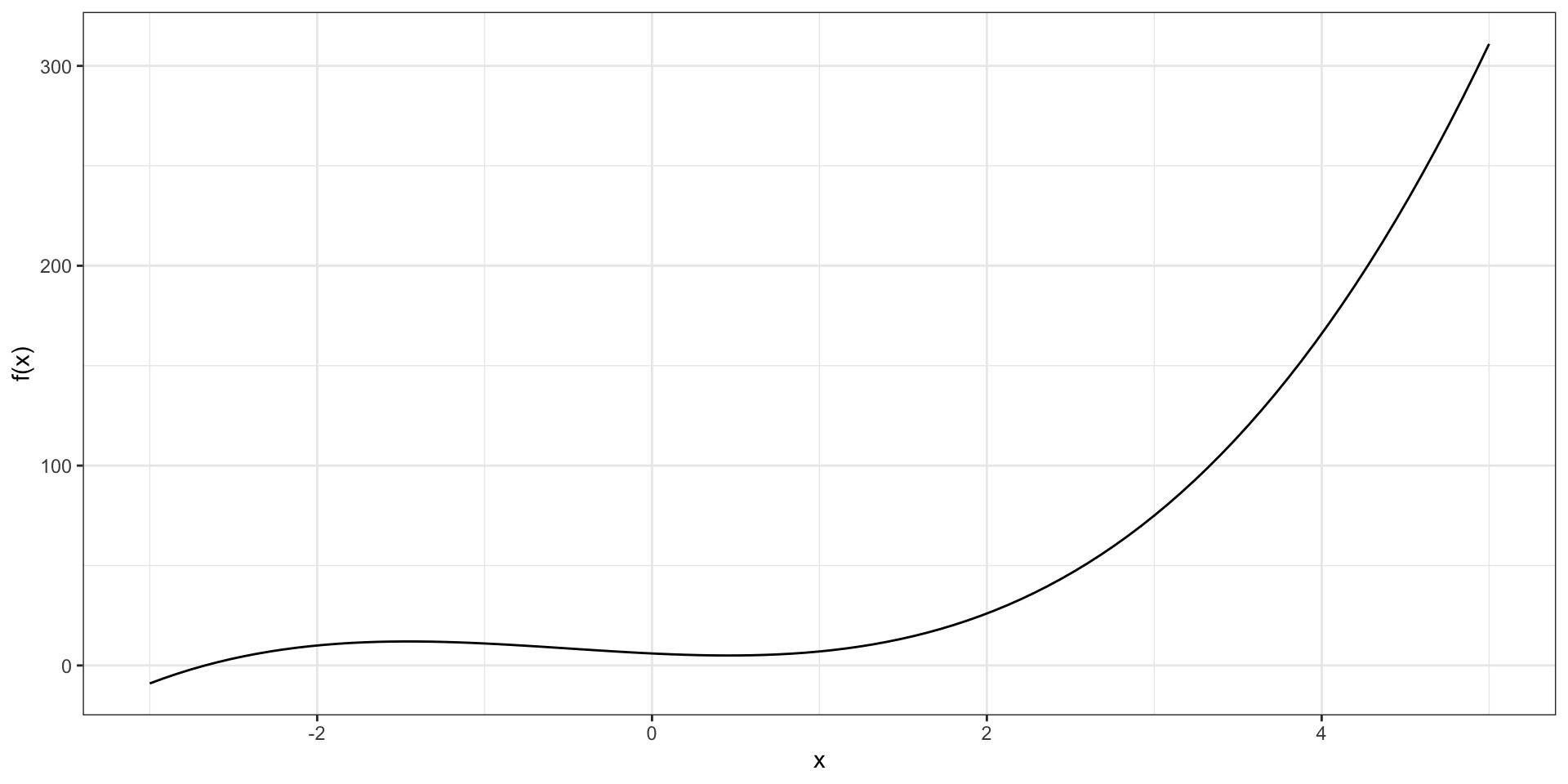
Логика производной
Выберем точку \(x_0\), в которой мы хотим определить, куда и с какой скоростью движется наша функция. В этой точке функция имеет значение \(y_0\):
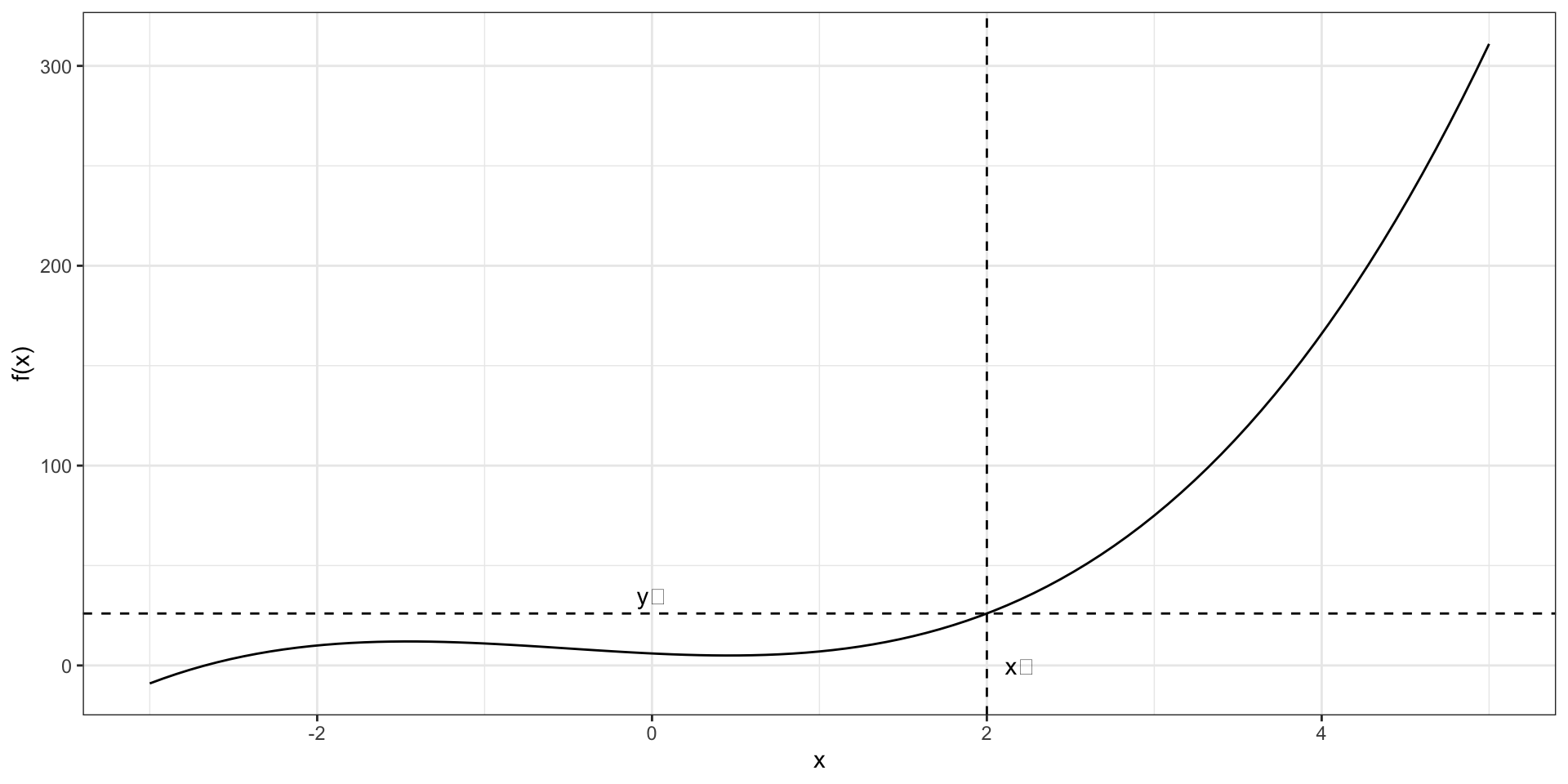
Логика производной
Шагнём на некоторую дистанцию \(\Delta x\) вправо (по направлению оси \(x\)). Назовём эту дистанцию приращением аргумента. В точке \(x_0 + \Delta x\) фунция будет иметь какое-то значение \(y_0 + \Delta y\), где \(\Delta y\) — приращение функции.
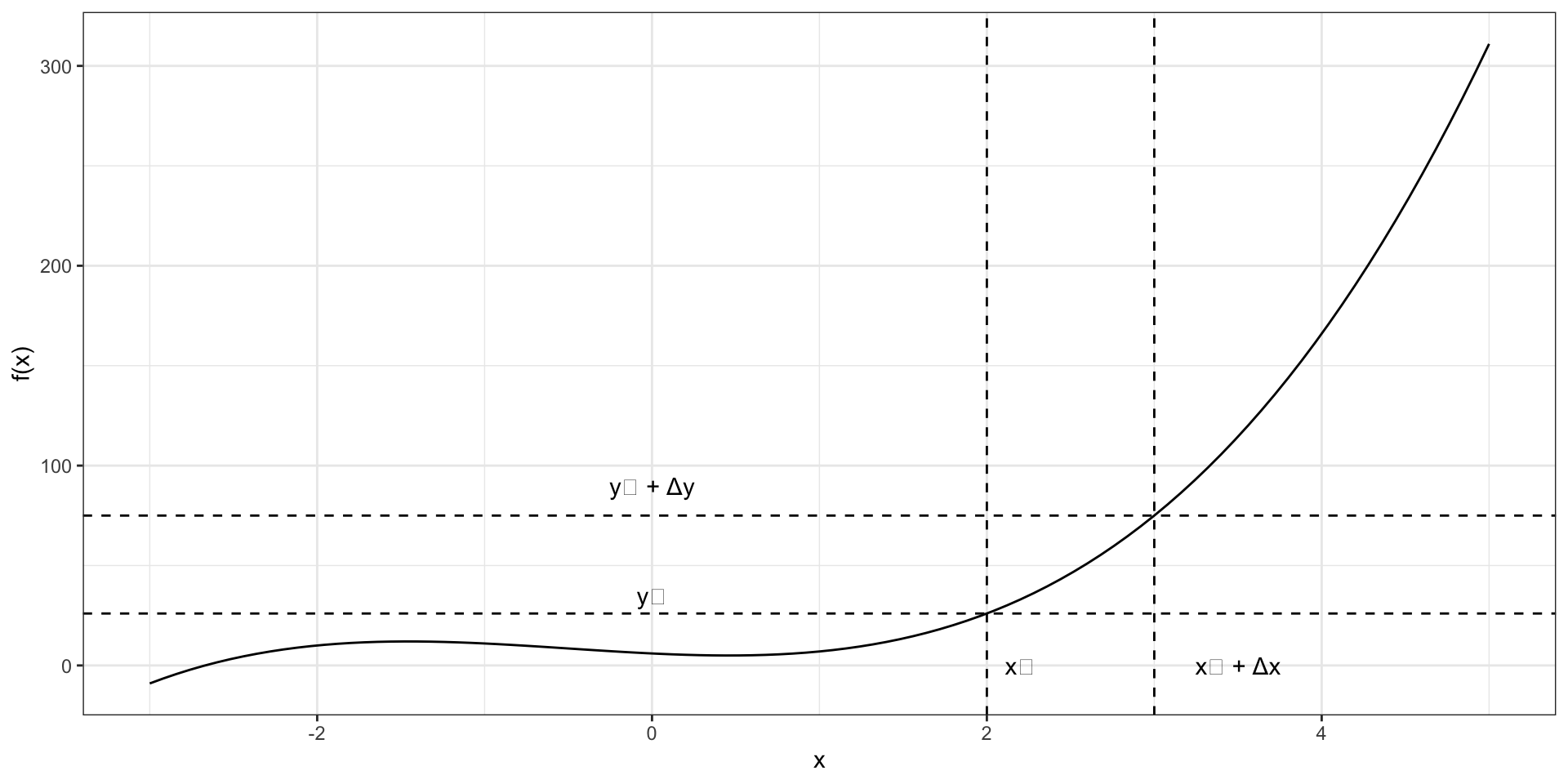
Логика производной
Наша функция движется из точки \((x_0,y_0)\) в точку \((x_0 + \Delta x, y_0 + \Delta y)\). Имеем следующий треугольник:
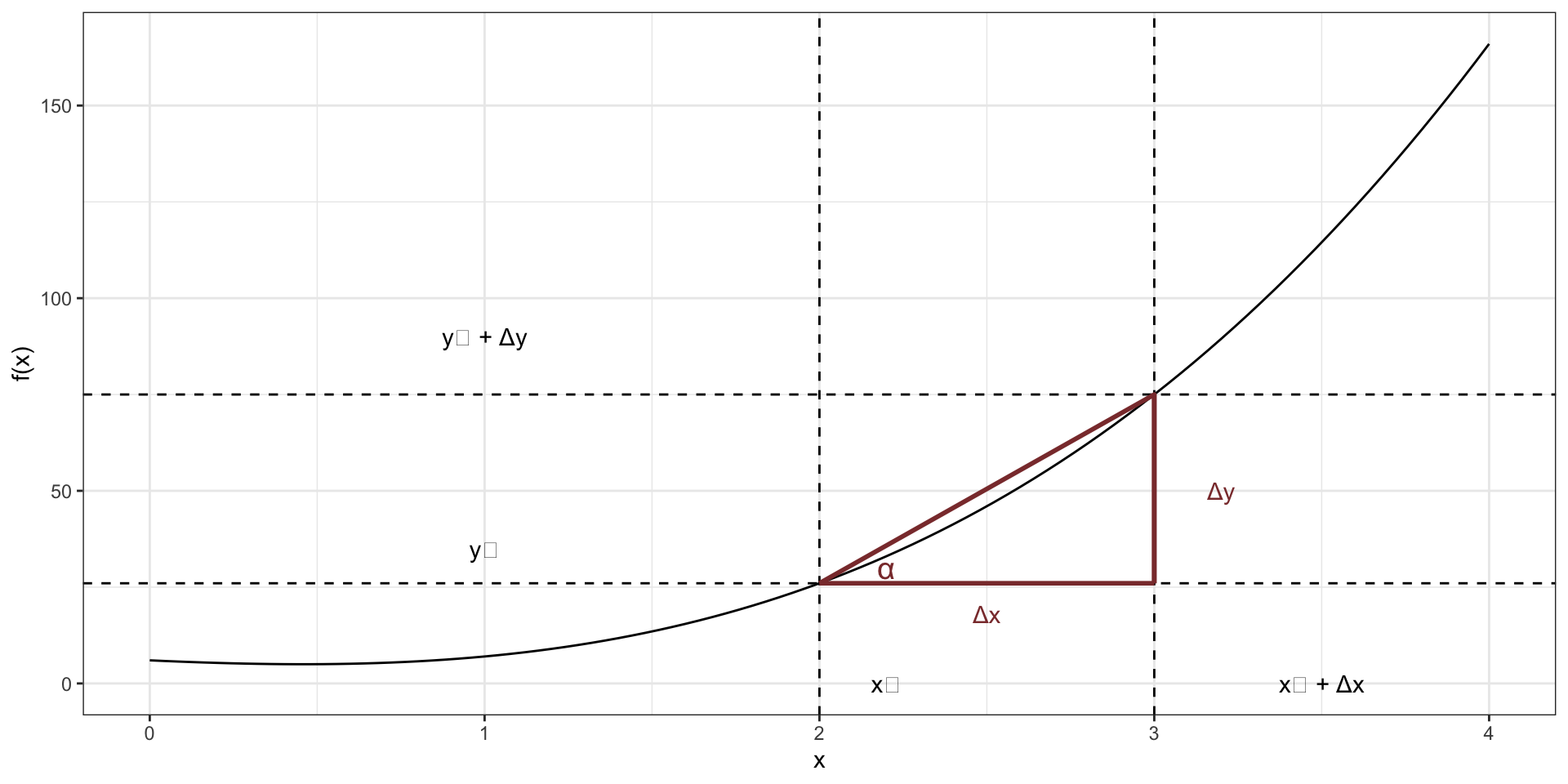
Логика производной
Нас интересует угол \(\alpha\) — именно он задает скорость и направление изменения функции. Если мы узнаем, каков угол \(\alpha\) — а точнее \(\tan \alpha\), потому что так проще — то узнаем, куда движется функция.
\[ \tan \alpha = \frac{\Delta y}{\Delta x} \]
Ну, хорошо. Но мы шагали достаточно далеко от точки, которая нас интесует. Если мы будем постепенно уменьшать шаг, то получим последовательность
\[ \langle \tan \alpha_1, \tan \alpha_2, \tan \alpha_3, ... \rangle \]
Логика производной
У этой последовательности есть предел, и если мы его рассчитаем, то как раз и получим значение производной в данной точке.
\[ f'(x_0) = \lim_{\Delta x \rightarrow 0} \frac{\Delta f_(x)}{\Delta x} = \frac{df}{dx}(x_0) \]
Очень маленькое приращение обозначается \(dx\) (или \(df\) , если это приращение функции). Вот мы и получили производную.
График производной
В точках, где график производной пересекает ось \(x\) — то есть там, где производная равна нулю — на исходной функции случаются точки смены монотонности — точки минимума и максимума.
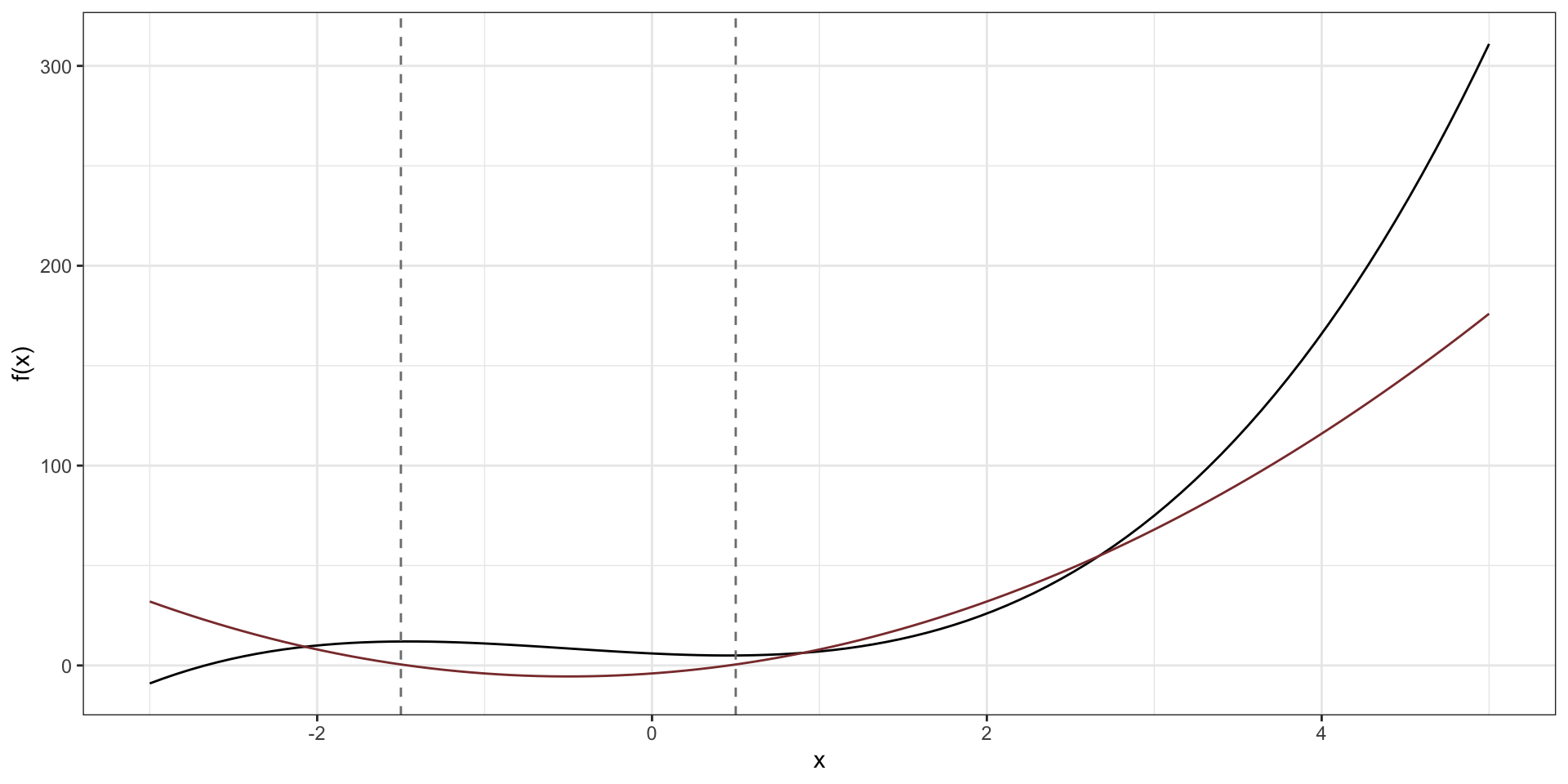
Функции нескольких переменных
Мы хорошо знакомы с функциями одной переменной, где некий \(y\) зависит от некоего \(x\) и более ни от чего не зависит. Однако в общем случае никто нам не может помешать задать следующую функцию:
\[ f(x, y) = 2x^2 + y^3 \]
Теперь у нас две переменные — \(x\) и \(y\) — и от них обоих зависит значение функции. Это даже можно изобразить:
Частная производная
- мы можем смотреть, как изменяются значения функции при изменении каждой переменной в отдельности
- для этого существуют частные производные.
- при взятии частной производной все другие переменные, по которым мы не берём производную в данный момент, считаются константами
Частная производная. Пример
Рассмотрим на примере нашей функции \(f(x, y) = 2x^2 + y^3\). Пусть мы хотим взять производную по \(x\). Тогда мы предполагаем следующее:
\[ y = \text{const}\Rightarrow y^3 = \text{const}= c \]
Фцнкция примет следующий вид:
\[ f(x, y) = 2x^2 + c, \]
а производная по \(x\) будет вычисляться следующим образом:
\[ \frac{\partial f(x, y)}{\partial x} = (2x^2 + c)' = (2x^2)' = 4x \]
Частная производная. Пример
Аналогично можно найти частную производную по \(y\):
\[ x = \text{const}\Rightarrow 2x^2 = \text{const}= c \]
\[ \frac{\partial f(x, y)}{\partial y} = (c + y^3)' = (y^3)' = 3x^2 \]
Знакомство с вычислением частной производной понадобится нам, чтобы понять, как внутри устроена линейная регрессия и ухватить идею градиентного спуска.
Площадь под графиком
Пусть у нас есть функция \(y = \sqrt{x}\). Нам надо найти площадь под её графиком на отрезке от \(0\) до \(3\).
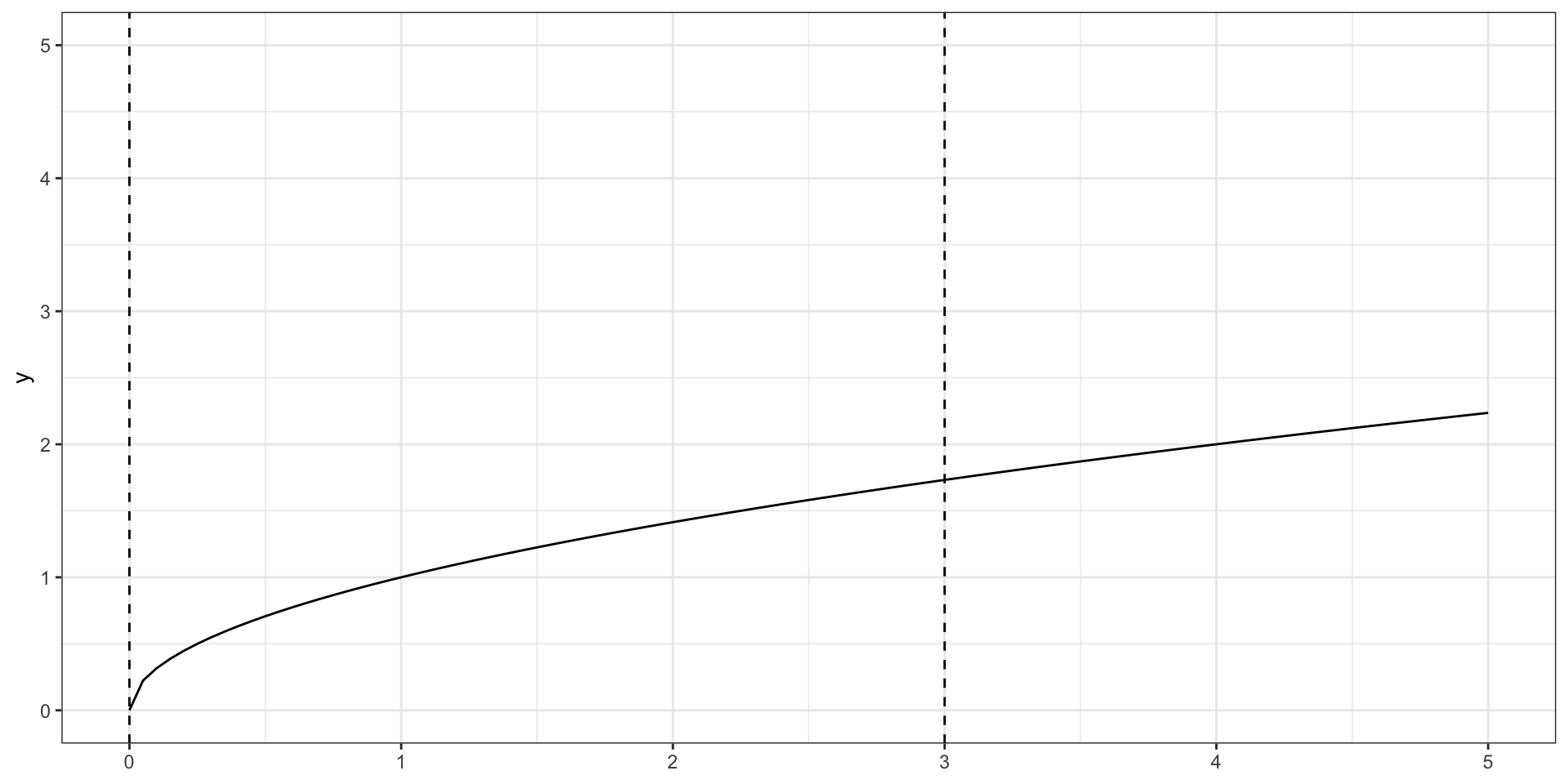
Площадь под графиком
Мы можем разбить этот отрезок на части размером \(\Delta x\), а саму площадь на соответствующие прямоугольники. Это нам позволит оценить площадь. На рисунке ниже \(\Delta x = 0.25\).
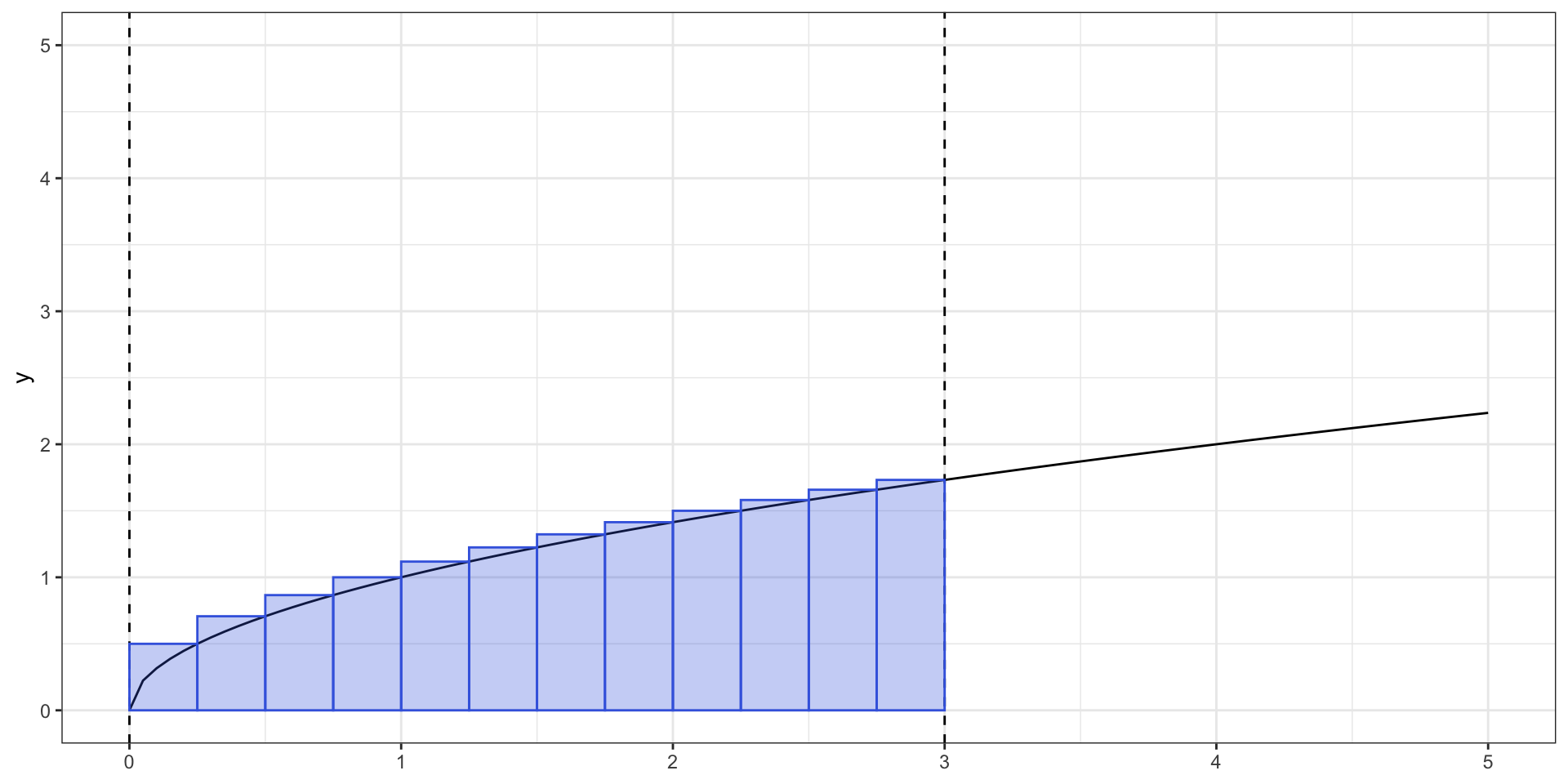
Площадь под графиком
Получается, площадь можно оценить, сложив площади всех прямоугольников:
\[ S \approx \sum_{i=1}^n y_i \Delta x \]
Чем более узкими прямоугольники у нас будут, тем точнее мы будем знать площадь. Ниже представлены рисунки для случая \(\Delta x = 0.1\) и \(\Delta x = 0.05\).
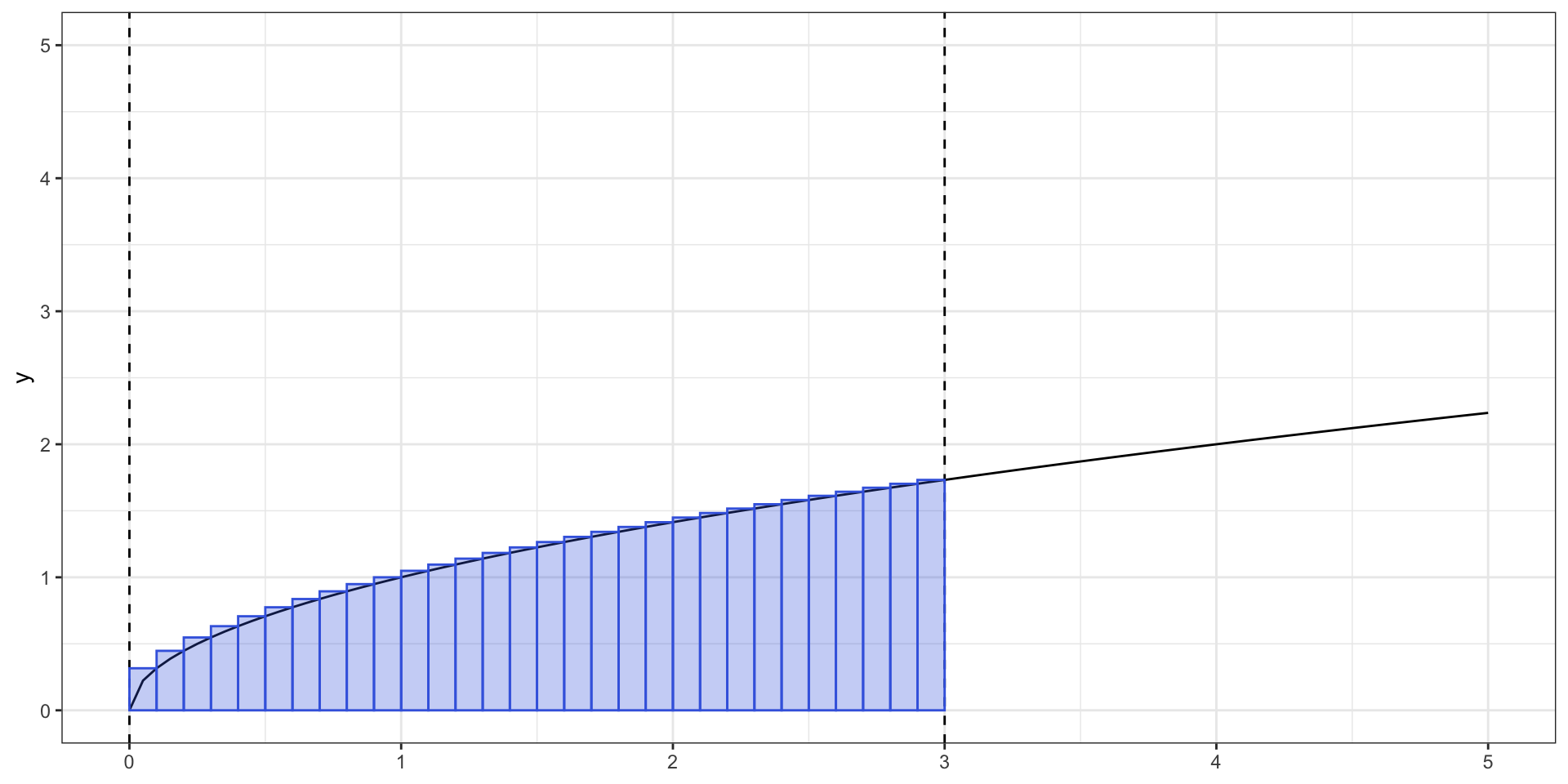
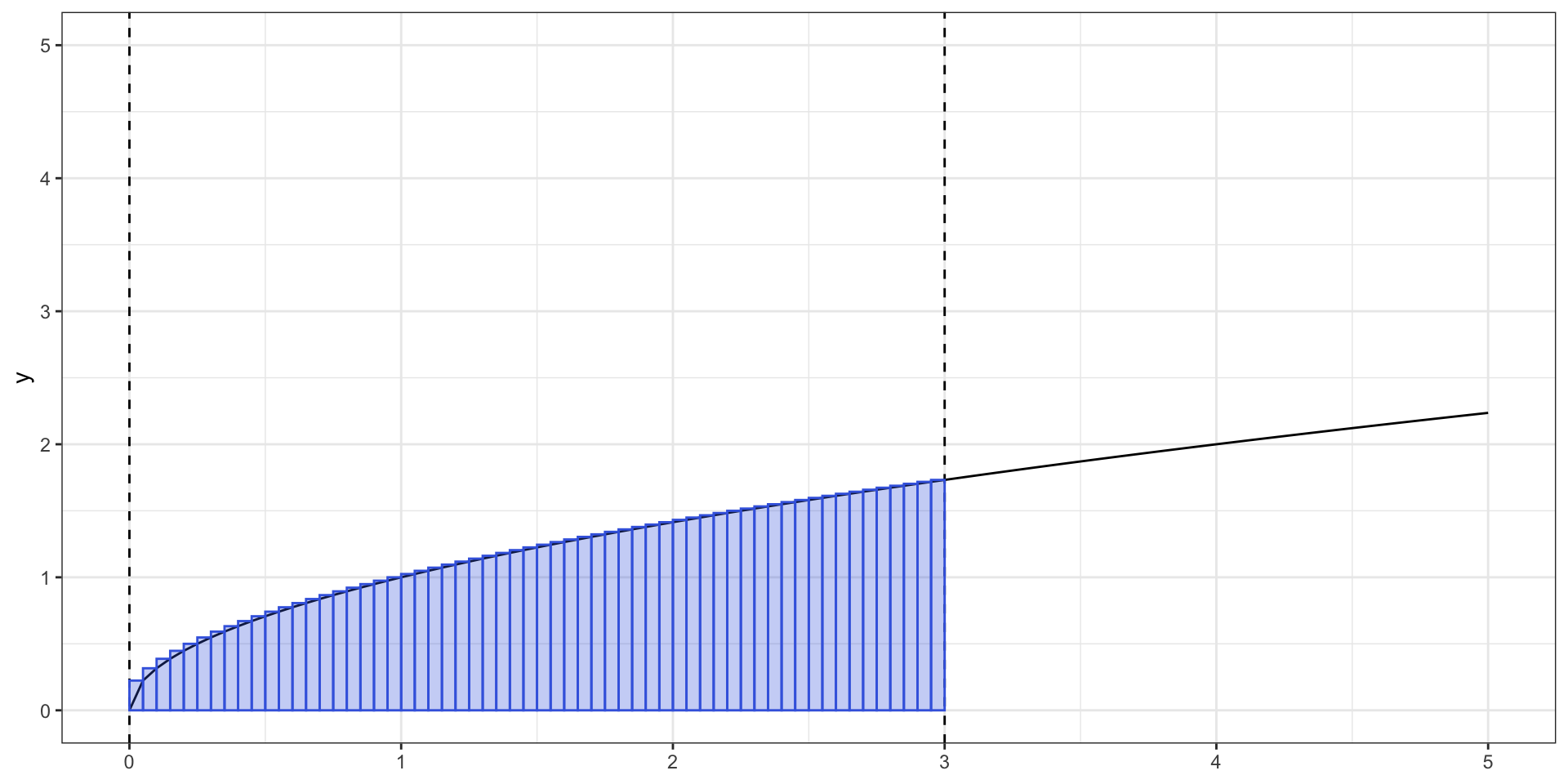
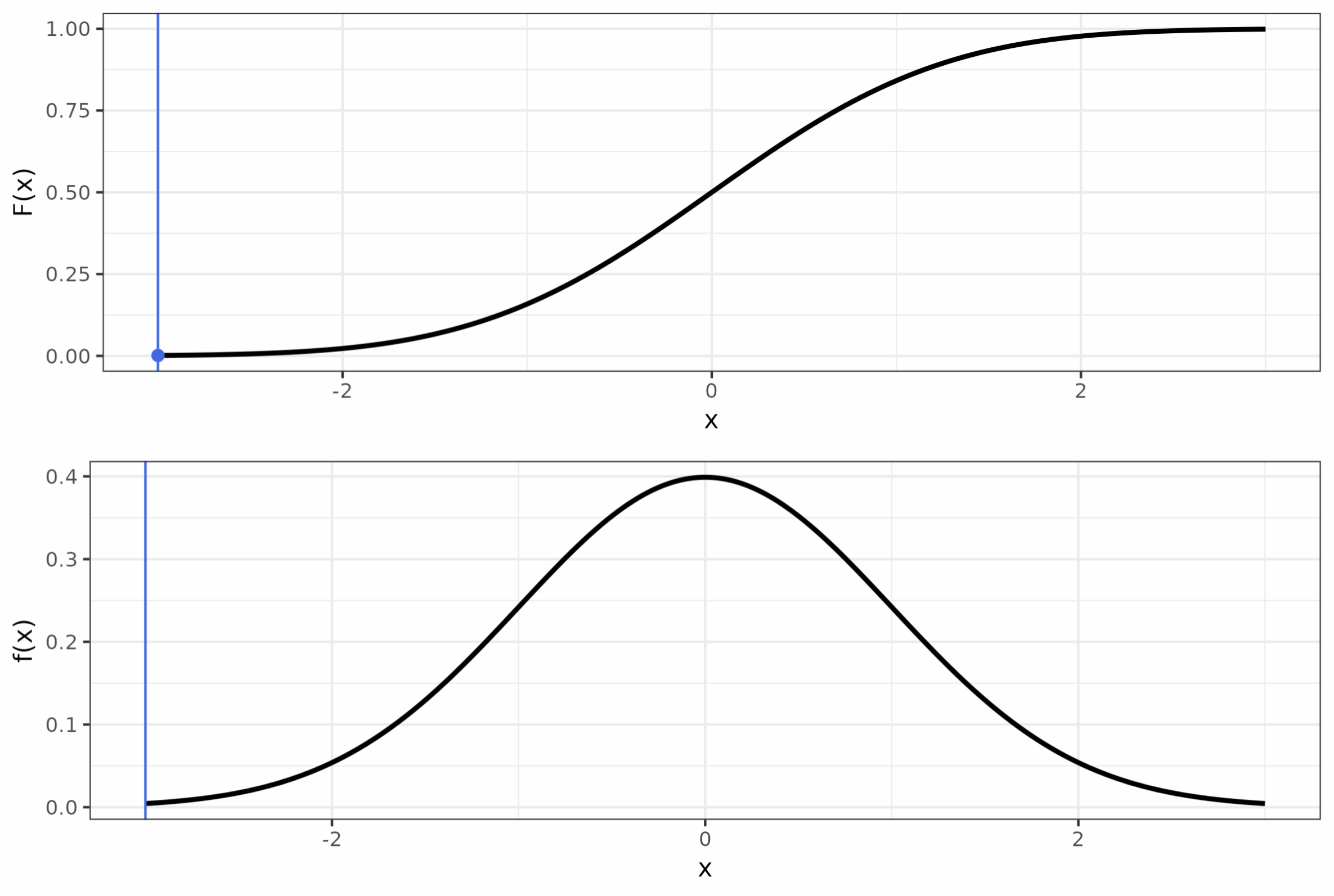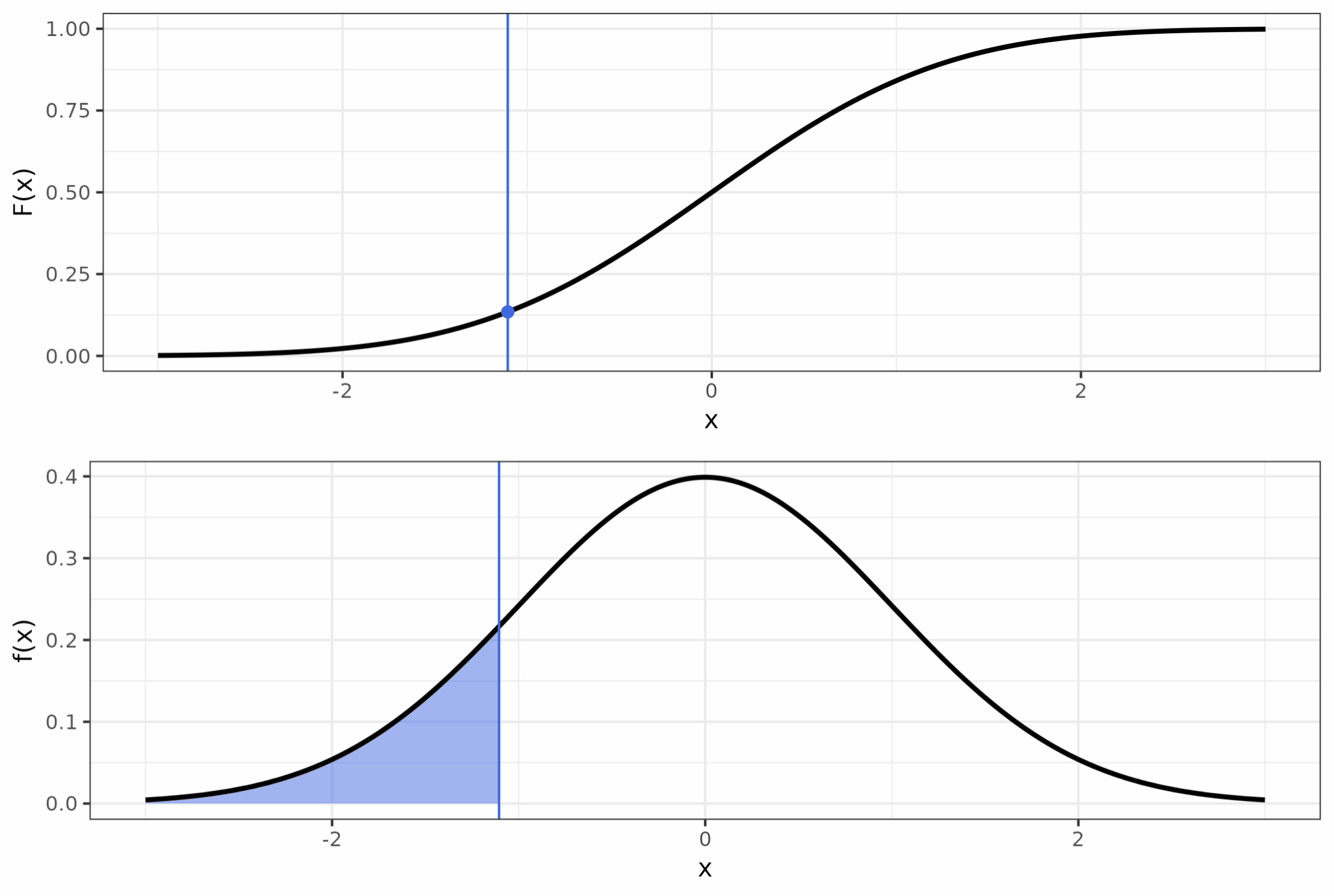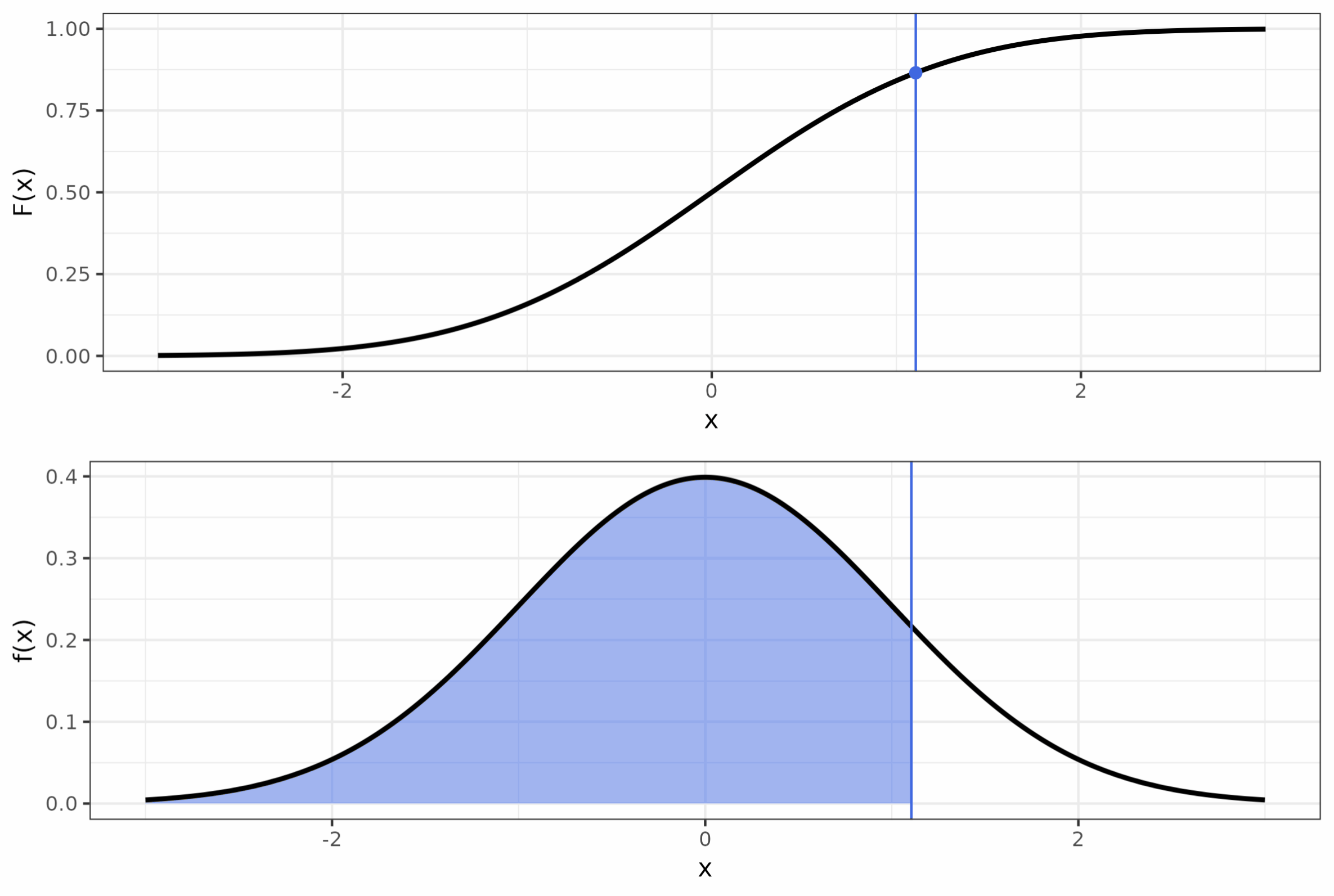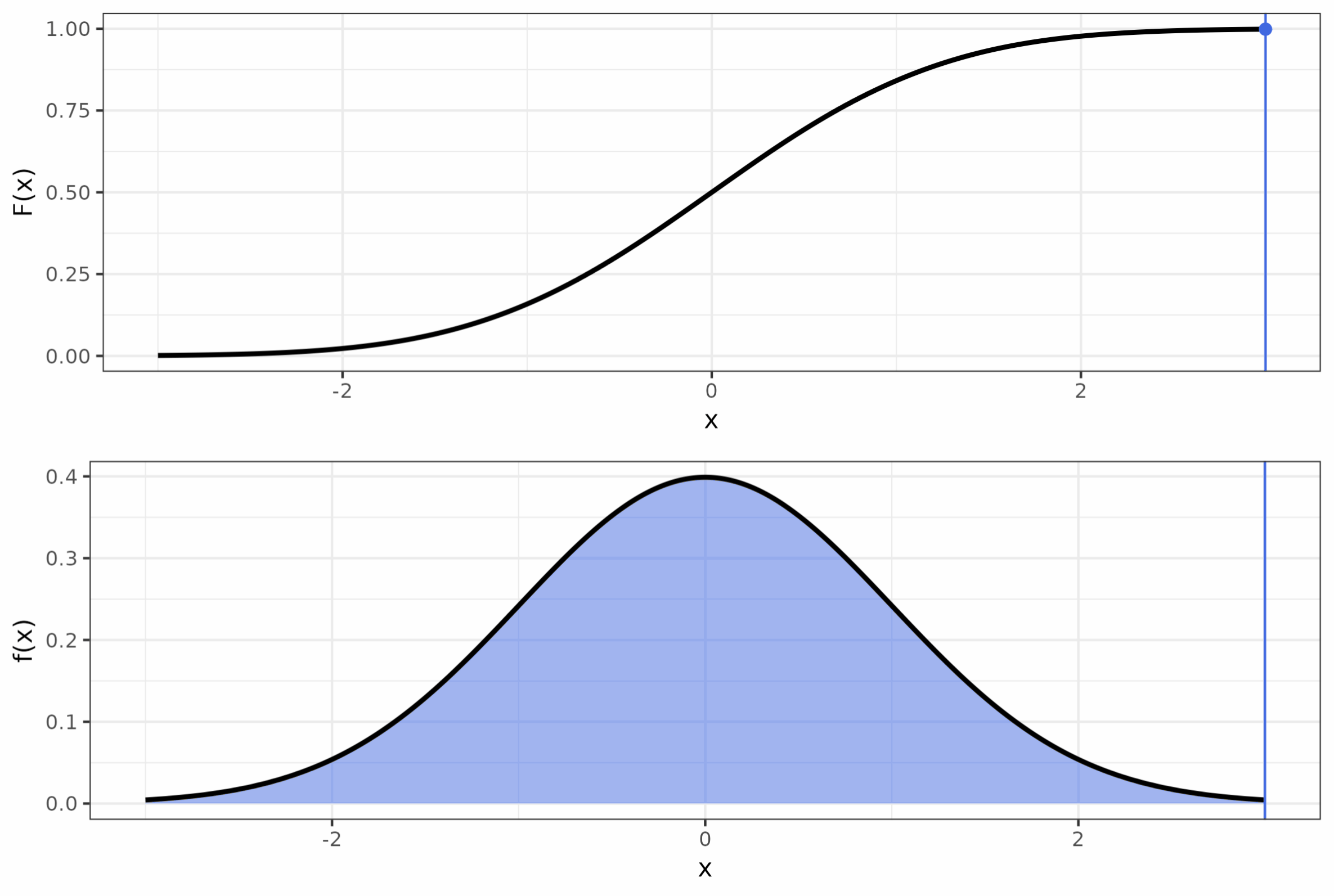
Определенный интеграл
Чтобы вычислить площадь точно, снова воспользуемся пределами, и определим с их помощью определенный интеграл:
\[ \lim_{\Delta x \rightarrow 0} \sum_{i = 1}^n y_i \Delta x = \int_a^b \sqrt{x}\,dx \]
Определенный он потому, что мы знаем, площадь в каких границах нас интересует. Определённый интеграл — это число.
\[ \int_0^3 \sqrt{x} \, dx \approx 3.46 \]
Неопределенный интеграл
Неопределённый интеграл (первообразная) — это такая функция \(F(x)\), производная которой \(F'(x)\) равняется \(f(x)\), то есть исходной функции. Таким образом, справедливо равенство
\[ F'(x) = f(x) \]
\[ \int_a^b f(x) dx = F(b) - F(a) \]
L3.3 // Элементы линейной алгебры
Системы линейных уравнений
\[ \cases{ a_{11}x_1 + a_{12}x_2 + \cdots + a_{1m}x_m = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2m}x_m = b_2 \\ \cdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nm}x_m = b_n \\ } \]
\[ \mathbf{A}\mathbf{x} = \mathbf{b} \]
\[ \mathbf{A} = \pmatrix{ a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} } \quad \mathbf{x} = \pmatrix{x_1 \\ x_2 \\ \vdots \\ x_m} \quad \mathbf{b} = \pmatrix{b_1 \\ b_2 \\ \vdots \\ b_n} \]
Векторы
\[ \mathbf{r} = \pmatrix{r_1 & r_2 & r_3 & \dots & r_n} \] \[ \mathbf{c} = \pmatrix{c_1 \\ c_2 \\ c_3 \\ \vdots \\ c_m} \]
Сложение векторов
\[ \mathbf{v} = \pmatrix{v_1 & v_2 & v_3 & \dots & v_n} \]
\[ \mathbf{w} = \pmatrix{w_1 & w_2 & w_3 & \dots & w_n} \]
\[ \mathbf{v} + \mathbf{w} = \pmatrix{v_1 + w_1 & v_2 + w_2 & v_3 + w_3 & \dots & v_n + w_n} \]
Умножение вектора на число
\[ \alpha \cdot \mathbf{v} = \pmatrix{\alpha \cdot v_1 & \alpha \cdot v_2 & \alpha \cdot v_3 & \dots & \alpha \cdot v_n}, \quad \forall \alpha \in \mathbb{R} \]
Скалярное произведение векторов
\[ \mathbf{v} \cdot \mathbf{w} = v_1 w_1 + v_2 w_2 + v_3 w_3 + \dots + v_n w_n \]
В результате скалярного произведения векторов получается одно число.
Матрицы
\[ \mathbf{A} = \pmatrix{ a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} } \]
\[ \mathbf{A} = \pmatrix{ \mathbf{a_1} & \mathbf{a_2} & \cdots & \mathbf{a_m} \\ } \]
\[ \mathbf{A} = \pmatrix{ \mathbf{a_1} \\ \mathbf{a_2} \\ \cdots \\ \mathbf{a_n} } \]
Матрицы
Матрица характеризуется размером. В размере сначала указывается количество строк, затем — количество столбцов. Рассматриваемая нами матрица \(\mathbf{A}\) имеет размер \(n \times m\), что можно записать как \(\mathbf{A}_{n \times m}\).
- Если количество строк и столбцов в матрице совпадает, она называется квадратной.
- В матрице есть главная диагональ — слева сверху вправо вниз — и побочная диагональ — справа сверху влево вниз.
- Квадратная матрица, все элементы которой, кроме стоящий на главной диагонали, равны нулю, называется диагональной матрицей.
- Есть две замечательные матрицы: единичная \(\mathbf{I}\) (или \(\mathbf{E}\)) и нулевая \(\mathbf{O}\).
\[ \mathbf{I} = \mathbf{E} = \pmatrix{ 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \\ } \quad \mathbf{O} = \pmatrix{ 0 & 0 & \dots & 0 \\ 0 & 0 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 0 \\ } \]
Сложение матриц
\[ \mathbf{A}_{n \times m} + \mathbf{B}_{n \times m} = \pmatrix { a_{11} + b_{11} & a_{12} + b_{12} & \dots & a_{1m} + b_{1m} \\ a_{21} + b_{21} & a_{22} + b_{22} & \dots & a_{2m} + b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} + b_{n1} & a_{n2} + b_{n2} & \dots & a_{nm} + b_{nm} \\ } \]
Умножение матрицы на число
\[ \alpha \cdot \mathbf{A} = \pmatrix{ \alpha \cdot a_{11} & \alpha \cdot a_{12} & \alpha \cdot \cdots & a_{1m} \\ \alpha \cdot a_{21} & \alpha \cdot a_{22} & \cdots & \alpha \cdot a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ \alpha \cdot a_{n1} & \alpha \cdot a_{n2} & \cdots & \alpha \cdot a_{nm} } \quad \forall \alpha \in \mathbb{R} \]
Матричное умножение
- Матрицы можно матрично перемножить друг с другом, если у них совпадают внутренние размерности.
- Результатом перемножения \(\mathbf{A}_{n \times k} \times \mathbf{B}_{k \times m}\) является матрица \(\mathbf{C}_{n \times m}\).
- Элемент \(c_{ij}\) матрицы \(\mathbf{C}\) равен скалярному произведению \(i\)-го вектора-строки матрицы \(\mathbf{A}\) и \(j\)-го вектора-столбца матрицы \(\mathbf{B}\).
Визуально:
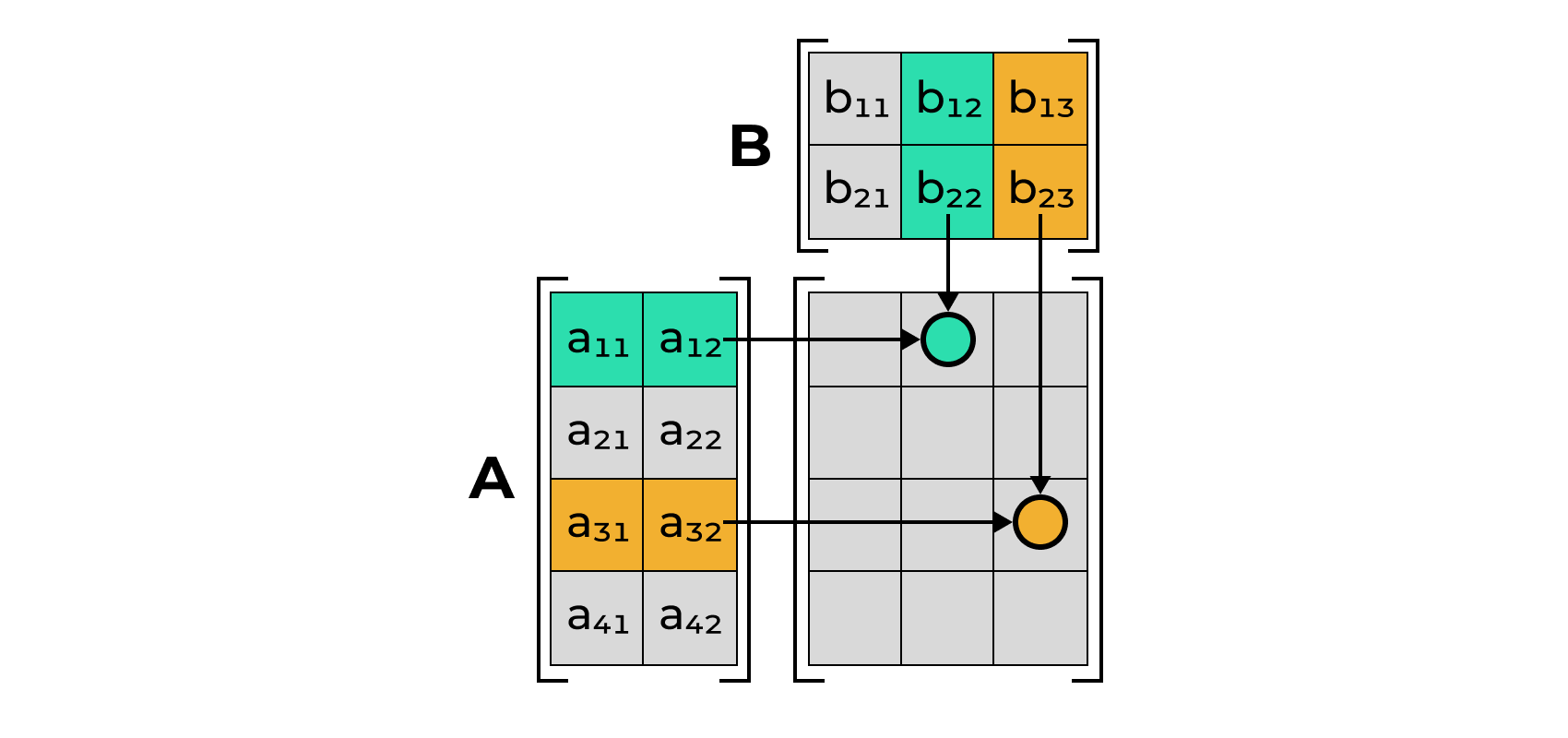
Матричное умножение
Пусть есть две матрицы \(\mathbf{A}_{n \times k} \times \mathbf{B}_{k \times m}\), которые выглядят следующим образом:
\[ \mathbf{A} = \pmatrix{\mathbf{a}_1 \\ \mathbf{a}_2 \\ \vdots \\ \mathbf{a}_n} = \pmatrix{ a_{11} & a_{12} & \dots & a_{1k} \\ a_{21} & a_{22} & \dots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nk} } \]
\[ \mathbf{B} = \pmatrix{\mathbf{b}_1 & \mathbf{b}_2 & \dots & \mathbf{b}_m} = \pmatrix{ b_{11} & b_{12} & \dots & b_{1m} \\ b_{21} & b_{22} & \dots & b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{k1} & b_{k2} & \dots & b_{km} } \]
\[ \mathbf{A} \times \mathbf{B} = \pmatrix{ \mathbf{a}_1 \cdot \mathbf{b}_1 & \mathbf{a}_1 \cdot \mathbf{b}_2 & \dots & \mathbf{a}_1 \cdot \mathbf{b}_m \\ \mathbf{a}_2 \cdot \mathbf{b}_1 & \mathbf{a}_2 \cdot \mathbf{b}_2 & \dots & \mathbf{a}_2 \cdot \mathbf{b}_m \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{a}_n \cdot \mathbf{b}_1 & \mathbf{a}_n \cdot \mathbf{b}_2 & \dots & \mathbf{a}_n \cdot \mathbf{b}_m \\ } = \]
\[ = \pmatrix{ (a_{11}b_{11} + a_{12}b_{21} + \dots + a_{1k}b_{k1}) & (a_{11}b_{12} + a_{12}b_{22} + \dots + a_{1k}b_{k2}) & \dots & (a_{11}b_{1m} + a_{12}b_{2m} + \dots + a_{1k}b_{km}) \\ (a_{21}b_{11} + a_{22}b_{21} + \dots + a_{2k}b_{k1}) & (a_{21}b_{12} + a_{12}b_{22} + \dots + a_{2k}b_{k2}) & \dots & (a_{21}b_{1m} + a_{22}b_{2m} + \dots + a_{2k}b_{km}) \\ \vdots & \vdots & \ddots & \vdots \\ (a_{n1}b_{11} + a_{n2}b_{21} + \dots + a_{nk}b_{k1}) & (a_{n1}b_{12} + a_{n2}b_{22} + \dots + a_{nk}b_{k2}) & \dots & (a_{n1}b_{1m} + a_{n2}b_{2m} + \dots + a_{nk}b_{km}) \\ } = \]
\[ = \pmatrix{ c_{11} & c_{12} & \dots & c_{1m} \\ c_{21} & c_{22} & \dots & c_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \dots & c_{nm} } = \mathbf{C} \]
\[ c_{ij} = \sum_{t=1}^k a_{it}b_{tj} \]
Свойства матричного умножения
- Ассоциативность: \(\mathbf{A}(\mathbf{B}\mathbf{C}) = (\mathbf{A}\mathbf{B})\mathbf{C}\) и \(\alpha(\mathbf{A}\mathbf{B}) = (\alpha\mathbf{A})\mathbf{B} = \mathbf{A}(\alpha\mathbf{B})\)
- Дистрибутивность: \(\mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{B}\mathbf{C}\) и \((\mathbf{A} + \mathbf{B})\mathbf{C} = \mathbf{A}\mathbf{C} + \mathbf{B}\mathbf{C}\)
- Отсутствие коммутативности: в общем случае \(\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}\)
- Умножение на единичный элемент: \(\mathbf{I}\mathbf{A} = \mathbf{A}\), \(\mathbf{A}\mathbf{I} = \mathbf{A}\)
- Умножение на нулевой элемент: \(\mathbf{O}\mathbf{A} = \mathbf{O}\), \(\mathbf{A}\mathbf{O} = \mathbf{O}\)
- Умножение на обратный элемент — выполняется только для некоторых квадратных матриц (см. ниже): \(\mathbf{A}\mathbf{A}^{-1} = \mathbf{A}^{-1}\mathbf{A} = \mathbf{I}\)
Транспонирование матрицы
\[ \mathbf{A} = \pmatrix{\mathbf{a}_1 & \mathbf{a}_2 & \dots & \mathbf{a}_n} = \pmatrix{ a_{11} & a_{12} & \dots & a_{1k} \\ a_{21} & a_{22} & \dots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nk} } \]
\[ \mathbf{A}^T = \pmatrix{\mathbf{a}_1 \\ \mathbf{a}_2 \\ \vdots \\ \mathbf{a}_n} = \pmatrix{ a_{11} & a_{21} & \dots & a_{n1} \\ a_{12} & a_{22} & \dots & a_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1k} & a_{2k} & \dots & a_{nk} } \]
Определитель и обратная матрица
Определитель (детерминант) матрицы \(\det \mathbf{A}\), \(|\mathbf{A}|\), \(\Delta A\) — это величина, которая «определяет» свойства матрицы, в том числе одно из ключевых — её обратимость.
- Если матрица не является квадратной, то детерминант не определен.
- Если детерминант матрицы не равен нулю, то:
- система линейных уравнений, задаваемая данной матрицей имеет единственное решение
- для данной матрицы существует обратная матрица, обладающая следующим свойством — \(\mathbf{A}\mathbf{A}^{-1} = \mathbf{I}\).
- Если детерминан матрицы равен нулю, то система линейных уравнений имеет несколько решений.
- Одной из причин может быть линейная зависимость между столбцами или строками матрицы — то есть ситуация, при который один из столбцов (одна из строк) линейной выражается через другой (другую).
След матрицы
След матрицы — это сумма элементов главной диагонали (квадратной) матрицы.
\[ \text{tr}(\mathbf{A}) = \sum_i a_{ii} \]
Итоги
- Выяснили логические основы всего
- Узнали, что можно делать со множествами
- Разобрались с производной и интегралом
- Познали матрицы
L3 // Математика для анализа данных
Антон Ангельгардт

WLM 2023