L6 // Оценивание параметров в практике статистического анализа. Тестирование статистических гипотез
Что будет?
- Смысл оценивания параметров
- Точечные оценки
- Свойства точечных оценок
- Логика тестирования гипотез
- Ошибки I и II рода
- Проблема множественных сравнений
L6.1 // Оценивание параметров
Сложная ситуация
- генеральная совокупность
- признаки
- показатели
- параметры
Параметр (\(\theta\)) — относительно постоянная [от одной совокупности к другой] величина, харакретизующая генеральную совокупность по некоторому показателю.
величина параметра, который мы изучаем, неизвестна
выборочная совокупность (выборка)
выборочная характеристика, или оценка (\(\hat \theta\))
Основные характеристики статистических данных
Неопределённость — мы не знаем, что именно мы получим в результате наших измерений для конкретной выборки
Вариативность — наши данные будут различатся от выборки к выборке и от респондента к респонденту
Итог
нам не доступны истинные значения параметров
вынуждены использовать оценки этих параметров
Как нам получить эти оценки?
Какими свойствами они должны обладать, чтобы хорошо отражать параметры генеральной совокупности?
Точечные оценки
- Параметр генеральной совокупности \(\theta\)
- Точечная оценка \(\hat \theta\) функция (случайная величина) от результатов наблюдений:
\[ \hat \theta = \hat \theta (\mathbf{x}), \; \mathbf{x} = \pmatrix{ x_1 & x_2 & \dots & x_n} \]
IQ
- параметр — среднее значение
- признак — интеллект
- показатель — коэффициент IQ (\(X\))
- \(X \thicksim \mathcal N(100, 225)\)
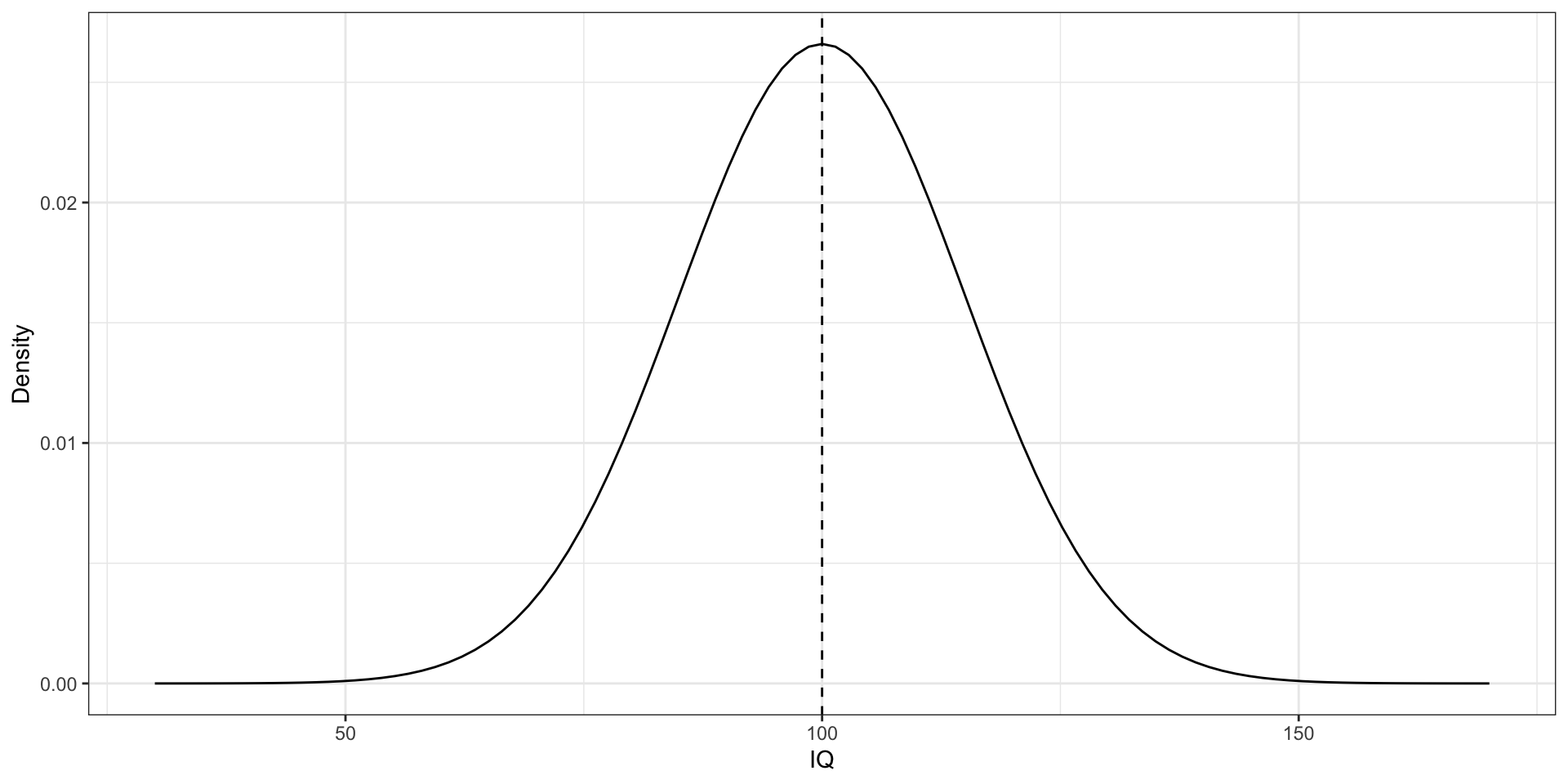
Извлекаем выборки
- \(n = 50\)
- оценки среднего (выборочные средние) \(\hat \mu\)
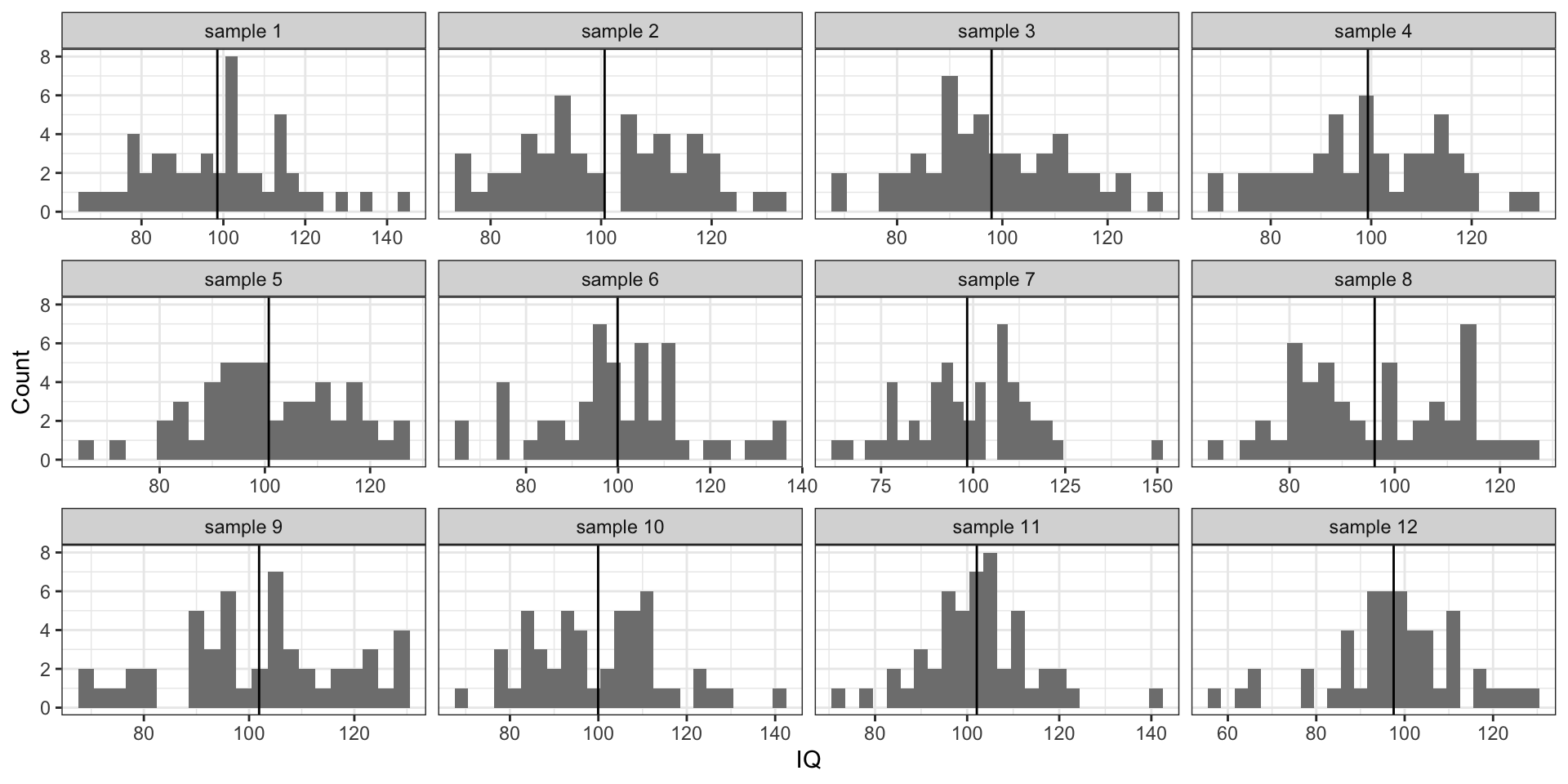
Метод моментов
В методе моментов есть три этапа:
- устанавливается связь между оцениваемым параметром и моментом распределения случайной величины
\[ \quad \theta = \xi(\mu_k), \]
где \(\mu_k\) — это момент случайной величины.
- находятся выборочные моменты
\[ \hat \theta = \xi(\mu_k^*) \]
- истинный момент заменяется на выборочный — получается оценка.
Метод моментов для математического ожидания
- среднее значение в случае генеральной совокупности — математическое ожидание
\[ \mu = \mathbb{E}X \]
- выборочный аналог математического ожидания — выборочное среднее [арифметическое]
\[ \hat \mu = \frac{1}{n} \sum_{i=1}^n x_i = \bar x \]
Свойства точечных оценок
- несмещённость
- состоятельность
- эффективность
Несмещенность
- когда мы постоянно используем выборочную оценку нашего параметра на выборках некоторого объема, мы в среднем не ошибаемся в оценке параметра.
\[ \forall n \; \mathbb{E} \hat \theta = \theta \] где \(n\) — объём выборок.
Несмещенность выборочного среднего
\[ \mathbb{E}(\bar X) \overset{?}{=}\mu \]
\[ X_1, X_2, \dots ,X_n \overset{\text{i.i.d}}{\thicksim} (\mu, \sigma^2) \]
\[ \mathbb{E}(\bar X) = \mathbb{E}\Big( \frac{1}{n} (X_1 + X_2 + \dots + X_n) \Big) = \frac{1}{n} \Big( \mathbb{E}(X_1) + \mathbb{E}(X_2) + \dots + \mathbb{E}(X_n) \Big) \]
\[ \mathbb{E}(\bar X) = \frac{1}{n} \cdot n \cdot \mu = \mu \]
Проверка несмещенности дисперсии
\[ \text{var}(X) = \mathbb{E}(X^2) - \big( \mathbb{E}X\big)^2 \]
\[ \text{var}(X) = \mathbb{E}(X - \mathbb{E}X)^2 = \frac{\sum_{i=1}^n(\mu - x_i)^2}{n} \]
Формулы эквивалентны:
\[ \begin{split} \text{var}(x) &= \mathbb{E}\big( (X - \mathbb{E}X )^2 \big) = \mathbb{E}\big( X^2 - 2 X \mathbb{E}X + (\mathbb{E}X)^2 \big) = \\ & = \mathbb{E}(X^2) - 2 \mathbb{E}X \mathbb{E}X + (\mathbb{E}X)^2 = \mathbb{E}(X^2) - 2 (\mathbb{E}X^2) + (\mathbb{E}X)^2 = \\ & = \mathbb{E}(X^2) - (\mathbb{E}X^2) \end{split} \]
Проверка несмещенности дисперсии
\[ \text{var}(X) = \frac{\sum_{i=1}^n(\mu - x_i)^2}{n} \]
\[ \mathbb{E}(\hat \sigma^2) = \sigma^2 \]
\[ \begin{split} \mathbb{E}(\hat \sigma^2) & = \mathbb{E}\Big( \mathbb{E}(X^2) - (\mathbb{E}X)^2 \Big) = \\ & = \mathbb{E}\Big( \overline{X^2} - \bar X^2\Big) = \mathbb{E}(\overline{X^2}) - \mathbb{E}(\bar X^2) \end{split} \]
\(\mathbb{E}(\overline{X^2})\):
\[ \mathbb{E}(\overline{X^2}) = \mathbb{E}\Big( \frac{X_1^2 + X_2^2 + \dots + X_n^2}{n} \Big) = \frac{1}{n} \Big( \mathbb{E}X_1^2 + \mathbb{E}X_2^2 + \dots + \mathbb{E}X_n^2\Big) \]
\[ \mathbb{E}(\overline{X^2}) = \frac{1}{n} \cdot n \cdot \mathbb{E}(X_i^2) = \mathbb{E}(X_i^2) \]
\(\mathbb{E}(\bar X^2)\):
\[ \begin{split} \mathbb{E}(\bar X^2) &= \mathbb{E}\Big( \frac{X_1 + X_2 + \dots + X_n}{n} \Big)^2 = \\ & = \frac{1}{n^2} \mathbb{E}(X_1 + X_2 + \dots + X_n)^2 = \\ & = \frac{1}{n^2} \mathbb{E}(X_1^2 + X_2^2 + \dots X_n^2 + 2X_1X_2 + \dots + 2X_{n-1}X_n) = \\ & = \frac{1}{n^2} \mathbb{E}\Big( (X_1^2 + X_2^2 + \dots X_n^2) + (2X_1X_2 + \dots + 2X_{n-1}X_n) \Big) \end{split} \]
\[ \begin{split} \mathbb{E}(\bar X^2) & = \frac{1}{n^2} \cdot n \cdot \mathbb{E}(X_i^2) + \frac{1}{n^2} \cdot \frac{n(n-1)}{2} \cdot 2 \mathbb{E}(X_iX_j) = \\ & = \frac{1}{n} \mathbb{E}(X_i^2) + \frac{n-1}{n} (\mathbb{E}X_i)^2 \end{split} \]
\[ \begin{split} \mathbb{E}(\hat \sigma^2) & = \mathbb{E}(\overline{X^2}) - \mathbb{E}(\bar X^2) = \\ & = \mathbb{E}(X_i^2) - \frac{1}{n} \mathbb{E}(X_i^2) - \frac{n-1}{n} (\mathbb{E}X_i)^2 = \\ & = \frac{n}{n} \mathbb{E}(X_i^2) - \frac{1}{n} \mathbb{E}(X_i^2) - \frac{n-1}{n} (\mathbb{E}X_i)^2 = \\ & = \frac{n-1}{n} \Big ( \mathbb{E}(X_i^2) - (\mathbb{E}X_i)^2 \Big) = \\ & = \frac{n-1}{n} \sigma^2 \end{split} \]
Оценка дисперсии является смещенной
- математическое ожидание нашей оценки оказывается равно не самому значению интересующего нас параметра, а значению параметра, умноженному на некоторое число \(\frac{n-1}{n}\)
- оценка является смещенной
- для расчета дисперсии на выборке используется выборочная, или исправленная, дисперсия
Исправленная (выборочная) дисперсия
Если оценка дисперсии отличается от значения параметра в \(\frac{n-1}{n}\) раз, то надо домножить оценку на \(\frac{n}{n-1}\):
\[ s^2 = \frac{n}{n-1} \cdot \hat \sigma^2 = \frac{n}{n-1} \cdot \frac{1}{n} \sum (x_i - \bar x)^2 = \frac{1}{n-1} \sum (x_i - \bar x)^2 \]
Состоятельность
\[ \lim_{n \rightarrow \infty} \mathrm{P}(|\hat \theta - \theta| < \varepsilon) = 1, \, \varepsilon > 0 \]
- при неограниченном росте мощности выборки наша оценка стремится к истинному значению параметра
- с ростом выборки значение нашей оценки все реже выпадает из некоторого достаточно узкого интервала \((\theta - \varepsilon, \theta + \varepsilon)\)
Состоятельность графически
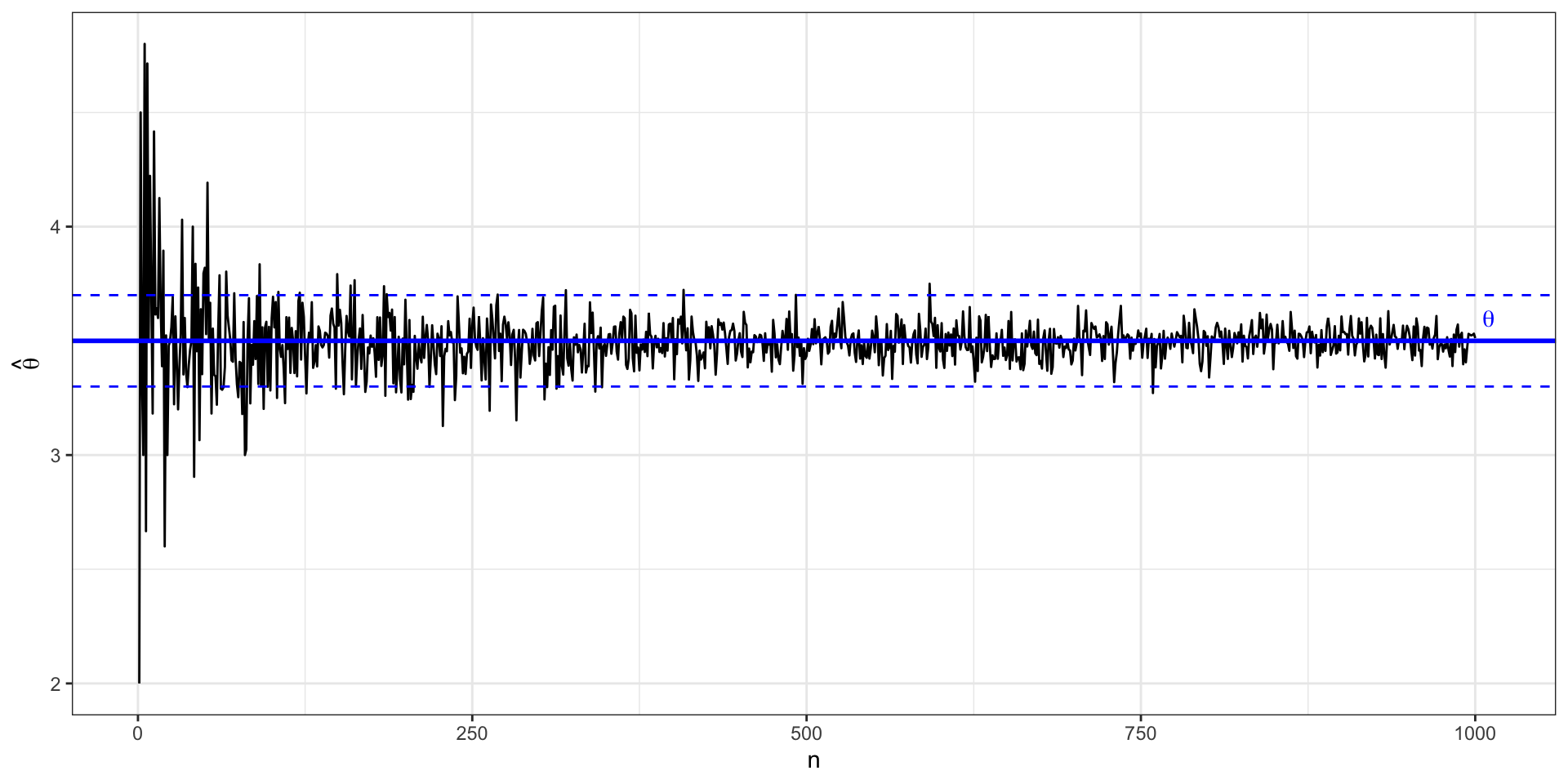
Несостоятельная оценка
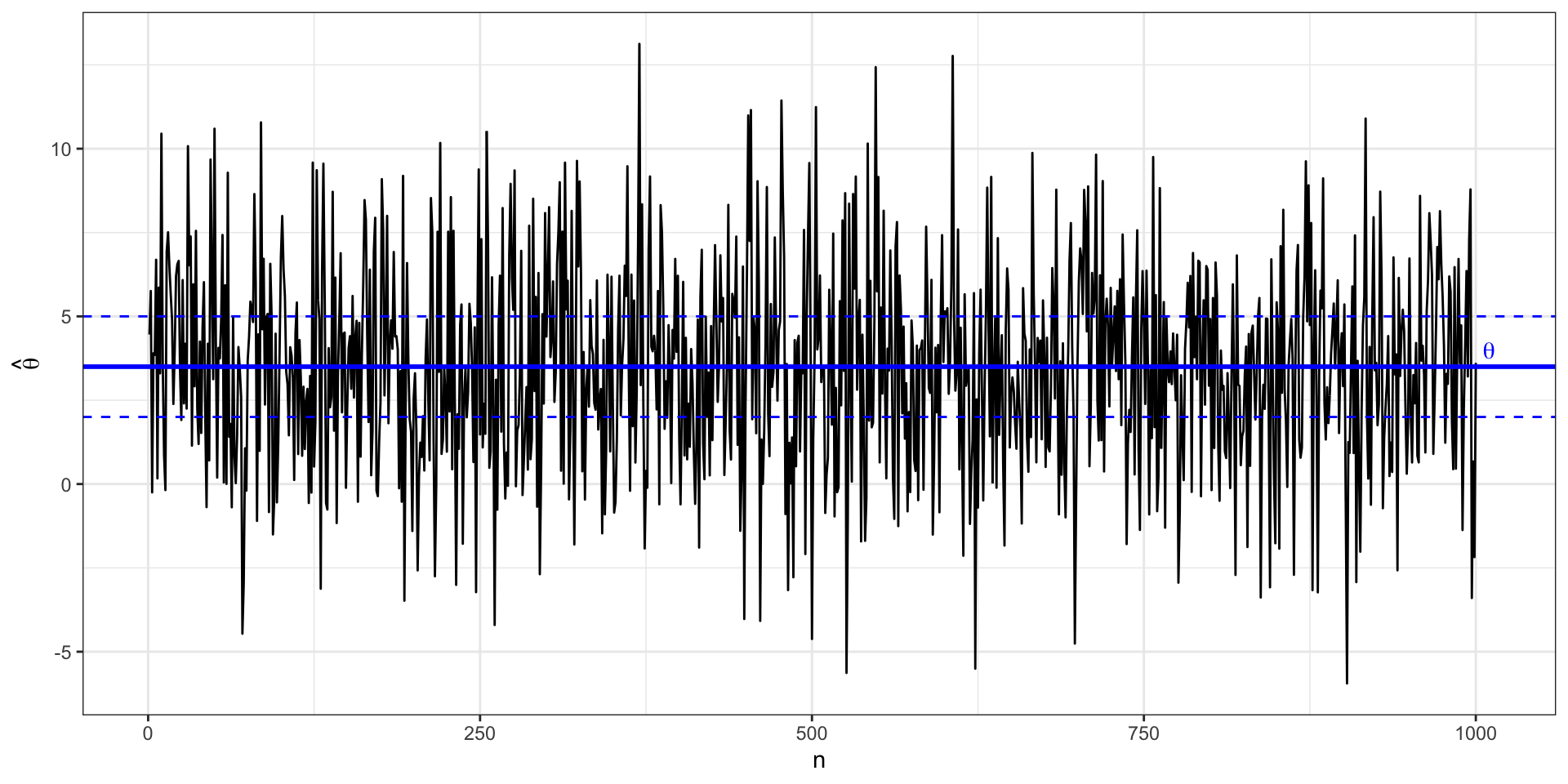
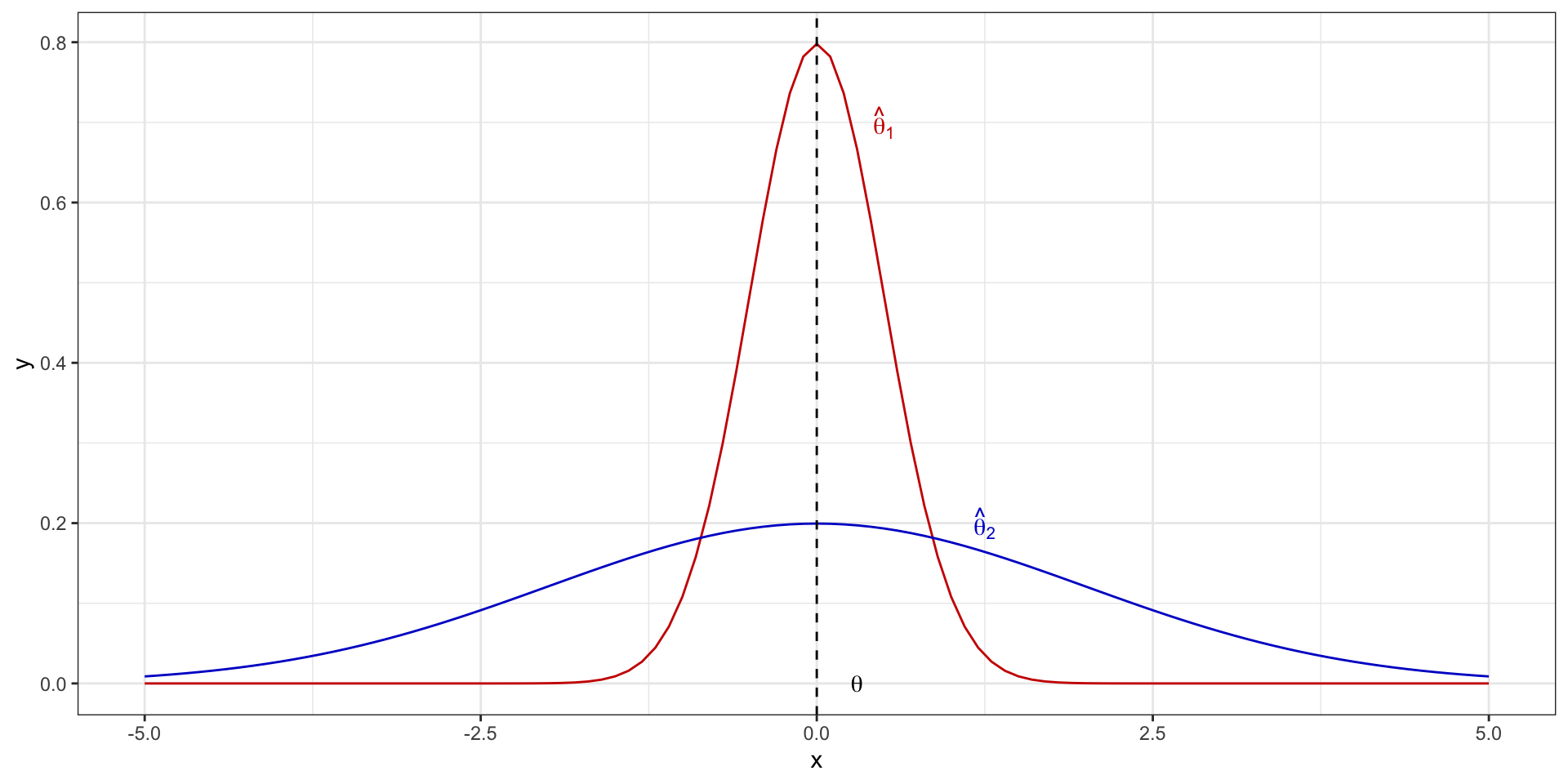
Эффективность
- оценка параметра — это случайная величина
- у неё есть дисперсия
- оценка эффективна, если её дисперсия минимальна
\[ \sigma^2_{\hat \theta} = \min \]
Эффективность графически
Интервальные оценки
Надёжность точечной оценки:
\[ \gamma = \mathbb{P}(\theta_\min < \theta < \theta_\max) \]
Такая форма оценки называется интервальной оценкой параметра, так как мы указываем интервал, в котором находится истинное значение с определённой вероятностью.
Стандартная ошибка
- IQ
- распределение параметра в генеральной совокупности такое
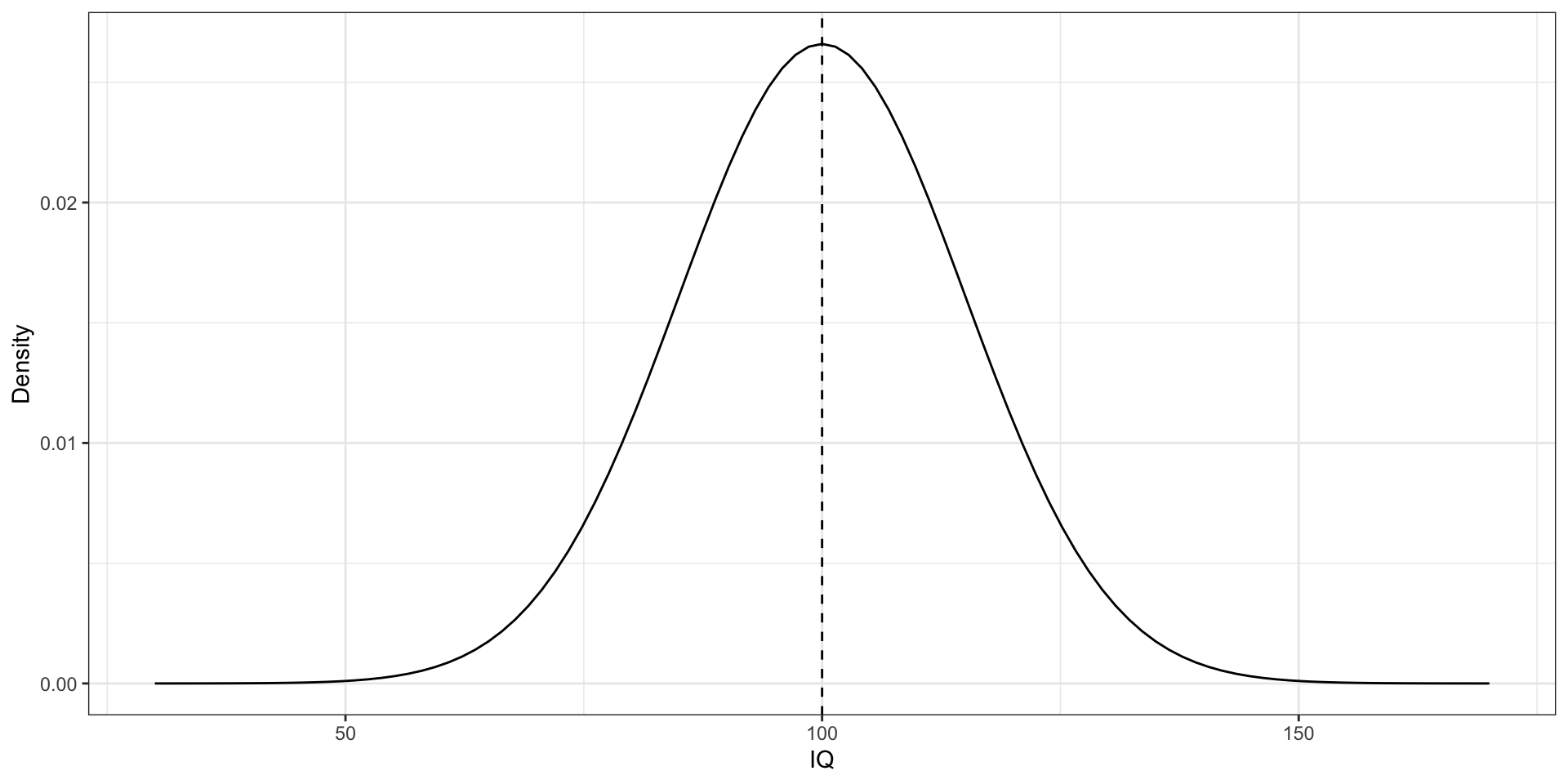
Стандартная ошибка
Вновь извлечем несколько выборок из нашей генеральной совокупности:
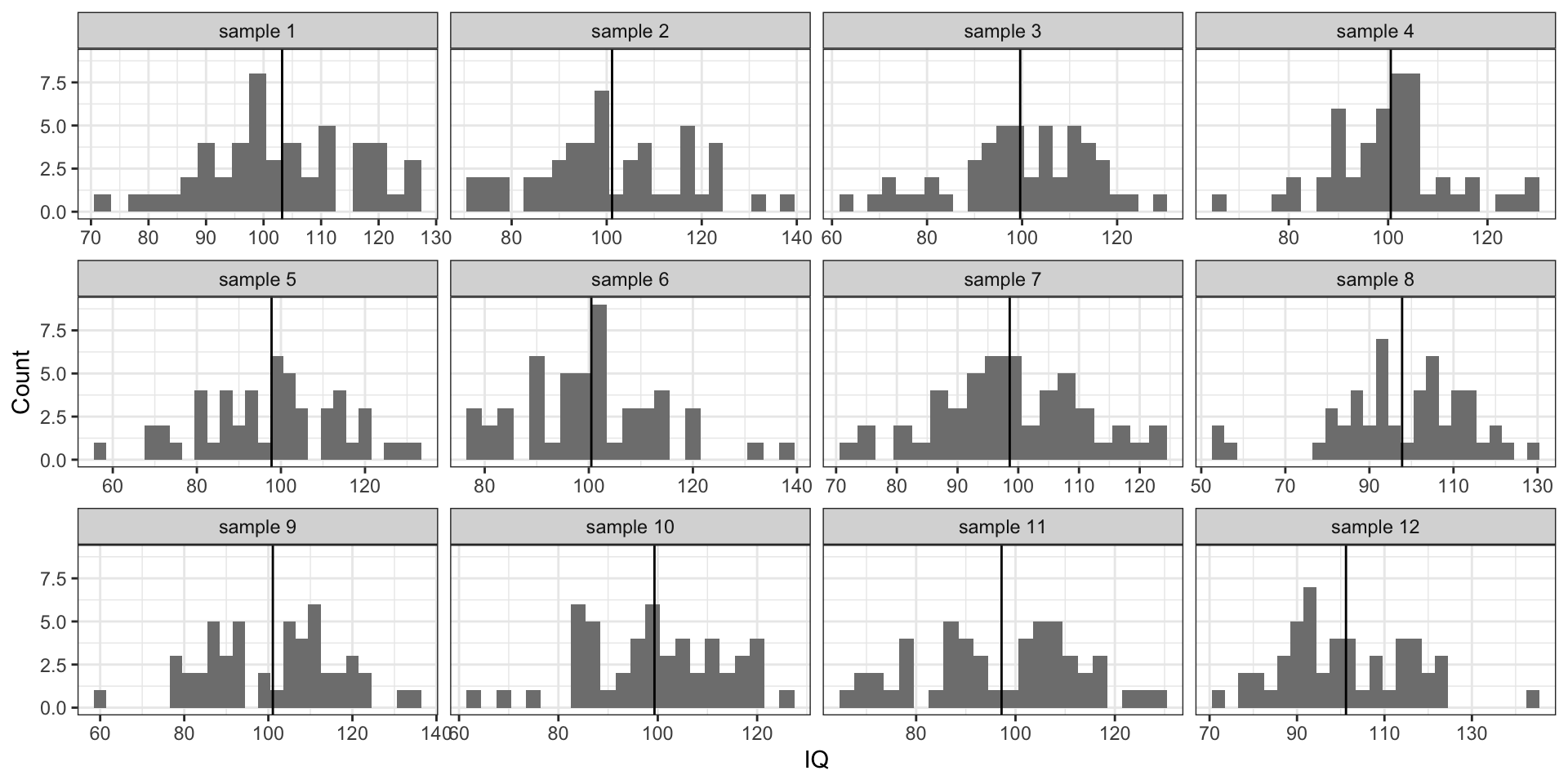
Стандартная ошибка
- извлечем 1000 выборок по 100 наблюдений
- посчитаем на каждой из них среднее
- построим распределение выборочных средних
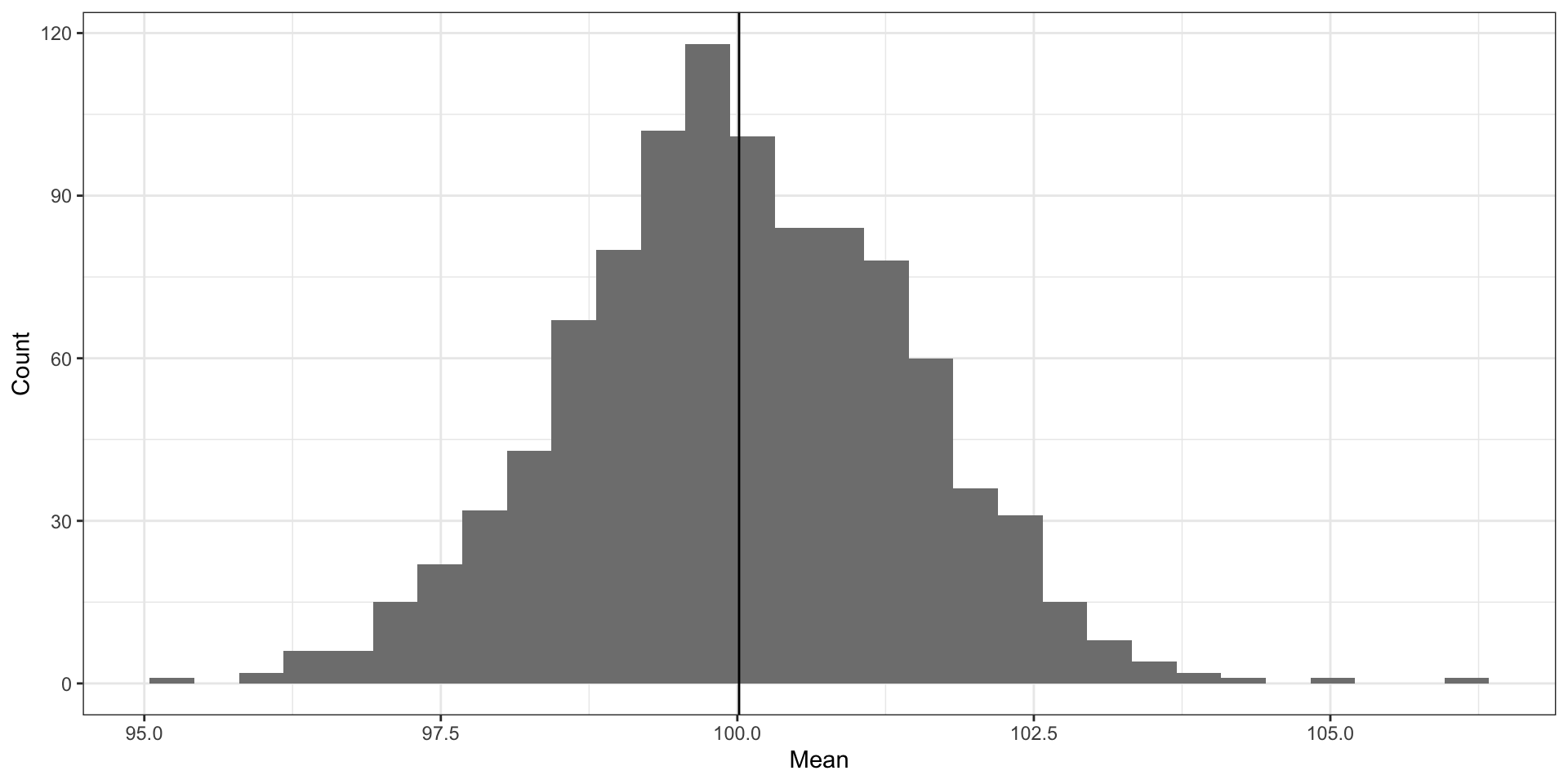
Распределение выборочных средних
\[ \mathcal N(\overline{\bar x}, \sigma_{\bar x}^2) \]
- среднее средних будет оказываться очень близко с значению нашего параметра
- cтандартное отклонение распределения выборочных средних называется стандартной ошибкой среднего (standard error of mean):
\[ \text{se}(\bar x) = \sqrt{\sigma^2_{\overline x}} = \sigma_{\overline x} \]
В нашем случае оно будет равно 1.43.
Стандартная ошибка как интервальная оценка
\[ \begin{split} 0.682 & = \mathbb{P}(\overline{\bar x}-\sigma_{\overline x} < \mu < \overline{\bar x}+\sigma_{\overline x}) \\ & = \mathbb{P}(98.57 < \mu < 101.43) \end{split} \]
Центральная предельная теорема
Расчет стандартной ошибки среднего
\[ \text{se}_X = \frac{\text{sd}_X}{\sqrt{n}} = \frac{\hat \sigma_X}{\sqrt{n}} \]
\[ \text{var}\bar X_i = \text{var}\Big( \frac{1}{n} \sum X_i \Big), \, X_i \overset{\text{i.i.d.}}{\thicksim} (\mu, \sigma^2) \]
\[ \begin{split} \text{var}\bar X_i & = \text{var}\Big( \frac{1}{n} \sum X_i \Big) \\ & = \frac{1}{n^2} \sum \text{var}(X_i) = \frac{1}{n^2} \sum \sigma^2 = \frac{n}{n^2} \sigma^2 = \frac{\sigma^2}{n} \end{split} \]
\[ \text{se}_X = \sqrt{ \text{var}\Big( \frac{1}{n} \sum X_i \Big)} = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}} \]
Доверительный интервал
\[ \mathrm{P}(\theta_\min < \theta < \theta_\max) = \gamma, \; \gamma \rightarrow 1 \]
\(\theta_\min\) и \(\theta_\max\) — границы доверительного интервала, \(\gamma\) — доверительная вероятность (обычно \(0.95\)).
Стандартное нормальное распределение
- \(z \thicksim \mathcal N(0, 1)\)
- \(\mathbb{P}(z \in [-1.96, 1.96]) = 0.95\)
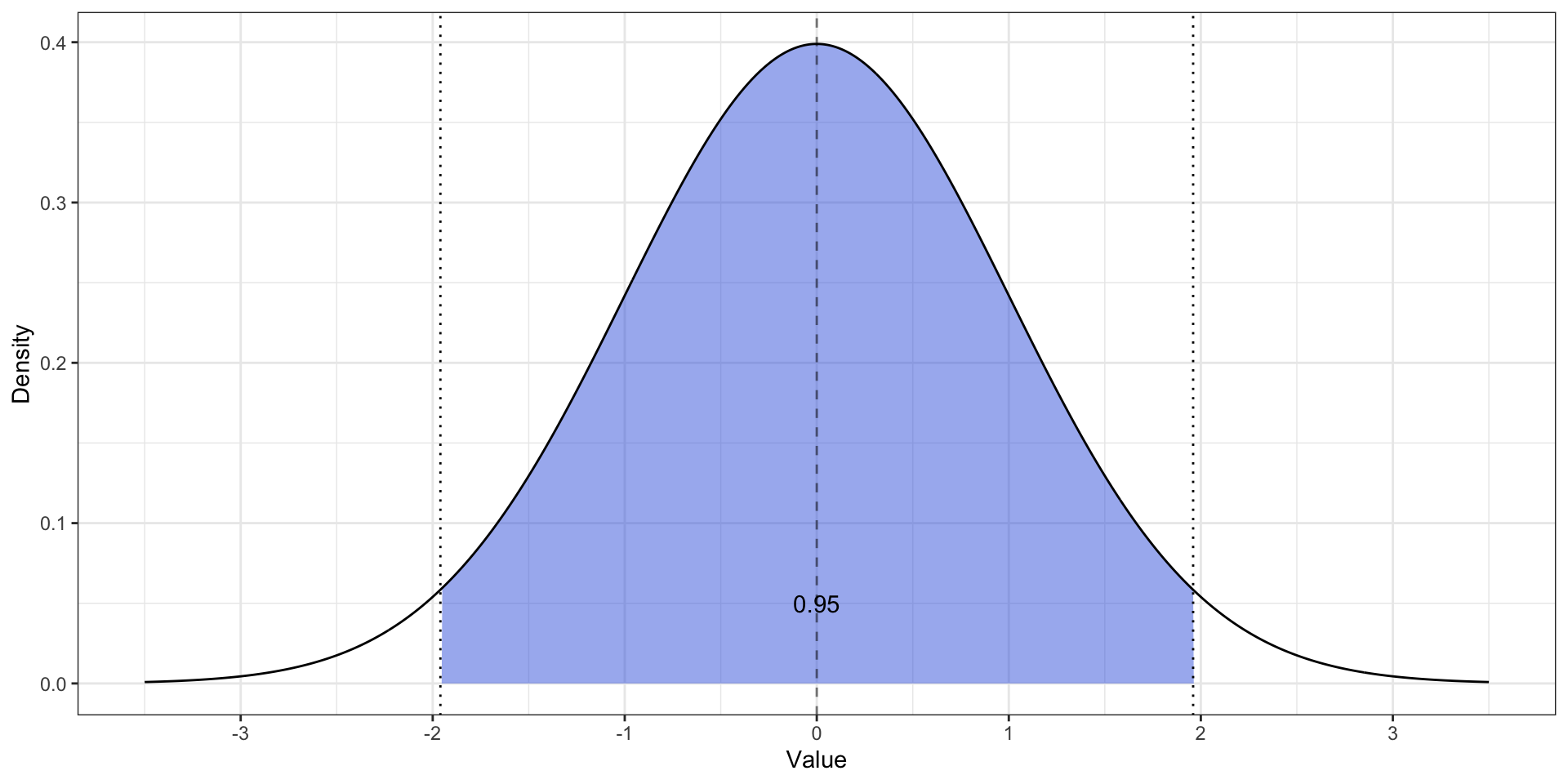
Вычисление доверительного интервала через стандартную ошибку
\[ \mathbb{P}\Big( \bar x + z_\min \text{se}_X < \mu < \bar x + z_\max \text{se}_X \Big) = \gamma \]
Для 95%-доверительного интервала:
\[ \mathbb{P}\Big( \bar x -1.96 \text{se}_X < \mu < \bar x + 1.96 \text{se}_X \Big) = 0.95 \]
Интерпретация доверительного интервала
Если мы будет бесконечно извлекать новые выборки из генеральной совокупности, рассчитывать на них средние и 95% доверительные интервалы к ним, то генеральное среднее попадёт в границы 95% таких доверительных интервалов.
Вероятность, что значение параметра генеральной совокупности попадет в пределы конкретного доверительного, рассчитанного в данном исследовании, оказывается меньше — около 84.3%.
L6.2 // Тестирование гипотез
Вопросы к статистическим методам
- Различаются ли группы между собой?
- Значимо ли влияние какого-либо фактора? → Различаются ли группы между собой?
- Хороша ли та модель, которую мы построили? → Отличается ли она от нулевой модели?
Нулевая и альтернативная гипотезы
- Гипотеза (\(H\)) — это предположение, которое подлежит проверке на основе результатов наблюдений.
- Гипотезы бывают:
- теоретические — про конструкты
- эмпирические — про переменные
- статистические — про параметры [генеральной совокупности] и данные
Статистические гипотезы
Простая гипотеза — \(H : \theta = \theta_0\) или \(H : \theta_1 = \theta_2\)
Сложная гипотеза — \(H : \theta > \theta_0\) или \(H : \theta_1 \neq \theta_2\).
Проверяемая (нулевая) гипотеза — \(H_0\)
Альтернативная гипотеза — \(H_1\)
Подходы к тестированию статистических гипотез
Фреквентистский подход
Какова вероятность получить такие данные, если допустить, что нулевая гипотеза верна?
Байесовский подход
Насколько вероятна справедливость нулевой или альтернативной гипотезы при условии, что мы получили такие данные.
Возможные результаты проверки гипотез
| \(H_0\) | \(H_1\) | |
|---|---|---|
| \(\hat H_0\) | ✓ | Ошибка II рода |
| \(\hat H_1\) | Ошибка I рода | ✓ |
- Ошибка I рода возникает, когда в генеральной совокупности искомой закономерности нет, но мы в силу случайных флуктуаций в данных её нашли.
- Ошибка II рода возникает, когда в генеральной совокупности искомая закономерность есть, но мы в силу каких-либо причин её не нашли.
Контроль ошибок I и II рода
- Ошибка I рода — уровень значимости \(\alpha\)
- Ошибка II рода — статистическая мощность \(1-\beta\)
- размер выборки
- размер эффекта
Результаты тестирования гипотез через вероятности
| \(H_0\) | \(H_1\) | |
|---|---|---|
| \(\hat H_0\) | \(\mathrm P (\hat H_0 | H_0)\) | \(\mathrm P (\hat H_0 | H_1) = \beta\) |
| \(\hat H_1\) | \(\mathrm P (\hat H_1 | H_0) = \alpha\) | \(\mathrm P (\hat H_1 | H_1) = 1 - \beta\) |
- \(\alpha \rightarrow 0\)
\[ \mathrm P (\hat H_1) = \mathrm P (\hat H_1 | H_0) \cdot \mathrm P (H_0) = \alpha \cdot \mathrm P(H_0) \]
- \((1-\beta) \rightarrow 1, \, \beta \rightarrow 0\)
\[ \mathrm P (\hat H_0) = \mathrm P (\hat H_0 | H_1) \cdot \mathrm P (H_1) = \beta \cdot \mathrm P (H_1) \]
Связь ошибки первого и второго рода
\[ \alpha \rightarrow 0 \Rightarrow \beta \rightarrow 1 \]
\[ \begin{split} \beta \cdot \mathrm P (H_1) & = \mathrm P (\hat H_0) = \mathrm P (\hat H_0 | H_0) \cdot \mathrm P (H_0) \Rightarrow \\ \beta & = \frac{1}{\mathrm P (H_1)} \cdot \mathrm P (H_0) \cdot \mathrm P(\hat H_0 | H_0) \\ \beta & = \frac{1}{\mathrm P (H_1)} \cdot \big (1 - \mathrm P (H_1 | H_0)\big) = \frac{1}{\mathrm P (H_1)} \cdot \mathrm P (H_0) \cdot (1 - \alpha) \end{split} \]
Асимметрия статистического вывода
Критерий — правило, согласно которому гипотезу либо принимают, либо отклоняют. Статистика — величина, позволяющая протестировать гипотезу (непрерывная случайная величина). Критическая область — область отклонения гипотезы.
Критическая область может быть односторонней (при \(H_1:\theta > \theta_0\) или \(H_1: \theta < \theta_0\)) и двусторонней (при \(H_1:\theta \neq \theta_0\)). «Размер» критической области определяется уровнем значимости.
Статистический вывод
- Статистический вывод — заключение о том, получили ли мы подтверждение альтернативной гипотезы
- По структуре — импликация
Если значение статистики критерия попало в критическую область, то у нас есть основания отклонить нулевую гипотезу в пользу альтернативной
- Если значение нашей статистики, которое мы рассчитали на выборке, попало в критическую область, то мы говорим о том, что нулевая гипотеза отклоняется.
- Если значение нашей статистики, которое мы рассчитали на выборке, не попало в критическую область, то мы не получаем оснований для того, чтобы отклонить нулевую гипотезу. Однако мы также не получаем оснований, чтобы её «принять».
Агоритм тестирования статистических гипотез
Сценарий 1
- Формулировка гипотезы
- Выбор статистического критерия
- Выбор уровня значимости \(\alpha\)
- Построение закона распредления статистики критерия при условии, что нулевая гипотеза верна
- Определение границ критической области
- Расчёт выборочной статистики
- Определение, попадает ли наблюдемое значение статистики в критическую область и вынесение решения
Сценарий 2
- Формулировка гипотезы
- Выбор статистического критерия
- Выбор уровня значимости \(\alpha\)
- Построение закона распредлеения статистики критерия при условии, что нулевая гипотеза верна
- Расчёт выборочной статистики
- Расчёт достигнутого уровня значимости p-value
- Сопоставление \(\alpha\) и p-value и вынесение решения
Размер эффекта и статистическая мощность
- Ошибка второго рода соответствует ситуации, когда мы не обнаружили закономерность при условии, что закономерность в генеральной совокупности присутствует
- На эту вероятность влияет «размер» той закономерности — размер эффекта (effect size)
- Мы работаем с вероятностью \(1-\beta = \mathbb{P}(\hat H_1|H_1)\) — статистическая мощность (statistical power)
Статистическая мощность зависит от размера эффекта и объема выборки:
- Чем больше размер эффекта, тем меньшую по объему выборку нам необходимо набрать, чтобы достигнуть требуемой статистической мощности.
- Чем больше выборка, тем выше статистическая мощность исследования.
Проблема множественных сравнений
- \(\alpha = 0.05\) в одном сравнении
- вероятность сделать правильный вывод — \(1 - \alpha\)
- сравнения независимы
- вероятность сделать правильный вывод в \(m\) сравнениях — \((1 - \alpha)^m\)
Вероятность ошибиться хотя бы в одном сравнении:
\[ \mathbb{P}^′ = 1 - (1 - \alpha)^m \]
В случае трёх сравнений вероятность ошибиться получается:
\[ \mathbb{P}^′ = 1 - (1 - 0.05)^3 \approx 0.143 \]
Зависимость вероятности ошибки первого рода от количества сравнений
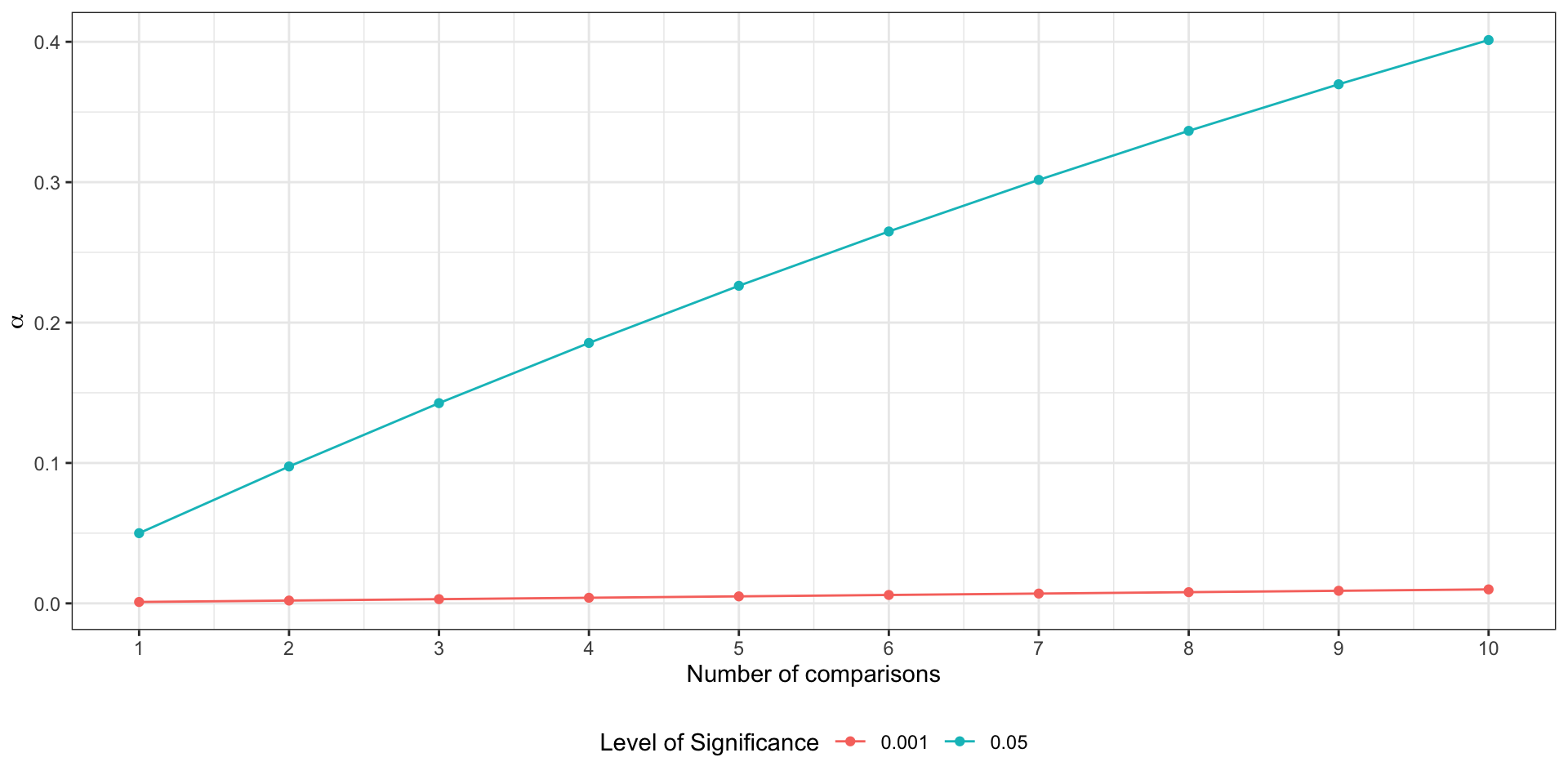
Корректировка уровня значимости
Поправка Бонферрони (Bonferroni):
\[ \alpha’ = \frac{\alpha}{n}, \]
где \(n\) — число попарных сравнений.
На практике в силу того, что в статистических пакетах мы работаем с p-value, корректируется именно его значение.
\[ p < \frac{\alpha}{n} \Rightarrow np < \alpha \]
Итоги
- Оценивание параметров методом моментов
- Несмещенность, состоятельность и эффективность — это найс
- Тестирование гипотез происходит по точному алгоритму
- Ошибки при тестировании гипотез случаются, и их нужно контролировать
- Ошибку I рода контролировать проще, чем ошибку II рода
- Если у нас несколько сравнений, то все становится грустно
L6 // Оценивание параметров в практике статистического анализа. Тестирование статистических гипотез
Антон Ангельгардт

WLM 2023