9 Анализ категориальных данных
Сегодня мы изучим первый статистический метод, которые применяется при анализе категориальных данных. Напомню, что это категориальные данные — это те, которые измерены в номинальной (реже — порядковой) шкале. А раз они измерены в номинальной шкале, значит наши данные разбиваются на некоторые категории. А раз есть категории, значит можно посчитать их частоты. А раз можно посчитать частоты, значит можно построить таблицу частот.
9.1 Таблица сопряженности
Таблицы частот для одной переменной мы с вами строили — это довольно простая задача. Однако теперь нас интересует не одна переменная, а две — мы будем искать связь между двумя категориальными переменными.
Давайте на примере. Пусть у нас есть данные о том, как студенты некоторого курса сдали экзамен по анализу данных. Экзамен проходил во вторник. При этом известно, что одна часть студентов усиленно готовилась к экзамену, а другая часть — отмечала понедельник в барах на Китай-городе.
В цифрах:
- всего студентов на курсе 120 человек
- успешно сдали экзамен 94 студента
- готовились к экзамену 86 студентов
- готовились и не сдали экзамен 3 студента
По этим данным мы можем построить таблицу сопряженности (contingency table, cross tabulation, crosstab).
| Сдали экзамен | Не сдали экзамен | ||
|---|---|---|---|
| Готовились | \(83\) | \(3\) | \(86\) |
| Отмечали понедельник | \(11\) | \(23\) | \(34\) |
| \(94\) | \(26\) | \(120\) |
Таблица сопряженности отражает совместное распределение двух категориальных (в данном случае — бинарных) переменных. На основе такой таблицы проверяеются гипотезы о связях между двумя категориальными переменными. В общем случае таблица сопряженности будет выглядеть так:
| \(X_1\) | \(X_2\) | ||
|---|---|---|---|
| \(Y_1\) | \(a\) | \(b\) | \(a+b\) |
| \(Y_2\) | \(c\) | \(d\) | \(c+d\) |
| \(a+c\) | \(b+d\) | \(N\) |
Эта таблица отражает эмпирические частоты — то есть те, которые получились из собранных нами данных. Здесь \(X\) и \(Y\) — наши переменные, индексы \(_1\) и \(_2\) показывают категорию, к которой относится то или иное наблюдение. На пересечении столбца и строки — частота совместного появления признаков \(X_i\) и \(Y_j\). Суммы частот по строкам и столбцам — маргинальные частоты [строк и столбцов соответственно].
Итак, эмпирические частоты у нас в наличии. Теперь вспомним алгоритм тестирования статистических гипотез:
- Формулировка гипотезы
- Выбор статистического критерия
- Выбор уровня значимости \(\alpha\)
- Построение закона распределения статистики критерия при условии, что нулевая гипотеза верна
- Расчёт выборочной статистики
- Расчёт достигнутого уровня значимости p-value
- Сопоставление \(\alpha\) и p-value и вынесение решения
Нам нужно сформулировать нулевую гипотезу. Как мы помним, нулевая гипотеза всегда об отсутствии каких-либо различий. В нашем случае если нет никакой связи между переменными \(X\) и \(Y\) — подготовка к экзамену и успешность сдачи — то все частоты в таблице должны быть равны. То есть
\[ H_0: a = b = c = d \]
Альтернативная гипотеза в этом случае будет гласить, что хотя бы между двумя какими-либо ячейчас отсутствует статистическое равенство. Это сложно записать математически — можно, но будет длинно. Воспользуется логическим отрицанием — неверно, что все частоты равны между собой:
\[ H_1: \neg(a=b=c=d) \]
Окей, формулировка гипотезы — ✓ done!
Теперь надо понять, как нам эту гипотезу протестировать. Мы бы, конечно, могли просто взять и сравнить наши частоты, но мы так делать не можем, ибо всё ещё вариативность и неопределенность статистических данных. Надо придумать другой ход.
Мы можем взять теоретическую ситуацию, когда между нашими переменными нет связи — а значит нет различия между частотами — и сравнить с тем, что у нас есть в таблице. Так и поступают. Поэтому сначала нам нужно рассчитать теоретические частоты.
9.2 Расчёт теоретических частот
Чтобы построить таблицу теоретического распределения частот, нам нужно понять, как были бы распределены наши данные в случае, если между нашими переменными не было бы связи. Это делается так:
| \(X_1^*\) | \(X_2^*\) | |
|---|---|---|
| \(Y_1^*\) | \(\frac{(a+b) \cdot (a+c)}{N}\) | \(\frac{(a+b) \cdot (b+d)}{N}\) |
| \(Y_2^*\) | \(\frac{(c+d) \cdot (a+c)}{N}\) | \(\frac{(c+d) \cdot (a+c)}{N}\) |
То есть для расчета теоретической частоты в конкретной ячейке мы перемножаем соответствующие маргинальные вероятности и делим на число наблюдений. Рассчитаем теоретические частоты для нашего примера:
| Сдали экзамен | Не сдали экзамен | |
|---|---|---|
| Готовились | \(\frac{86 \cdot 94}{120} = 67.37\) | \(\frac{86 \cdot 26}{120} = 18.63\) |
| Отмечали понедельник | \(\frac{34 \cdot 94}{120} = 26.63\) | \(\frac{34 \cdot 26}{120} = 7.37\) |
Чтобы понять, какое содержание стоит за расчетом теоретических частот, надо разложить расчет на два действия. Первое — вычисление долей сдавших и не сдавших экзамен:
\[ p_{\text{готовились}} = \frac{86}{120} \approx 0.72 \\ p_{\text{отмечали}} = \frac{34}{120} \approx 0.28 \]
Второе — находим части, равные рассчитанным долям, от количества сдавших и не сдавших экзамен:
\[ n_{\text{готовились и сдали}} = 0.72 \cdot 94 = 67.68 \\ n_{\text{готовились и не сдали}} = 0.72 \cdot 26 = 18.72 \\ n_{\text{отмечали и сдали}} = 0.28 \cdot 94 = 26.32 \\ n_{\text{отмечали и не сдали}} = 0.28 \cdot 26 = 7.28 \]
Ну, вот мы то же самое и получили [с точностью до промежуточного округления].
Итак, у нас есть всё, что нужно, чтобы перейти к тестированию гипотезы.
9.3 Критерий независимости Пирсона
Переходим ко второму пункту алгоритма — выбор статистического критерия. Для поиска взаимосвязей между категориальными переменными разработан критерий независимости Пирсона (\(\chi^2\) Пирсона). Это первый статистический критерий, с которым мы с вами знакомимся. У каждого статистического критерия есть статистика критерия, которая рассчитывается определенным образом. Для критерия \(\chi^2\) она рассчитывается так:
\[ \chi^2 = \sum_i \frac{(O_i - E_i)^2}{E_i}, \]
где \(O_i\) — эмпирические (наблюдаемые, observed) частоты, а \(E_i\) — теоретические (ожидаемые, expected) частоты.
Внимательно присмотревшись в формуле, можно увидеть, что чем больше отклонения эмпирических частот от теоретических, тем больше числитель дроби, тем больше статистистика критерия. Несложно рассчитать значения статистического критерия для нашего примера:
\[ \chi^2 = \frac{(83-67.37)^2}{67.37} + \frac{(3-18.63)^2}{18.63} + \frac{(11-26.63)^2}{26.63} + \frac{(23-7.37)^2}{7.37} \approx 59.06 \]
Дальше мы можем рассчитать критическое значения критерия \(\chi^2\) — договоримся, что если не оговорено иное, мы берем в качестве уровня значимости конвенциональный 0.05 — и сравнить его с полученным, но в прошлой главе мы договорились, что так делать не будем. Мы будем рассчитывать p-value, или достигнутый уровень значимости. Руками это делать трудно — надо в интегралы уметь и формулы для распределенрий знать — поэтому мы доверим это специально обученному программному обеспечению:
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: d
## X-squared = 55.378, df = 1, p-value = 9.946e-14Получилось другое значение \(\chi^2\), что связано со сделанными нами округлениями в ходе расчета теоретических частот. Но принципиально это ничего не меняет — мы видим p-value много меньше 0.05.
Как мы говорили в прошлой главе, если p-value меньше выбранного уровня значимости, у нас есть оcнования отклонить нулевую гипотезу об отсутствии различий, и принять альтернативную гипотезу. Итого, связь между подготовкой к экзамену и успешностью его сдачи есть. Ну, ничего себе какой полезный вывод — а мы то и не в курсе были…
Ладно, это всё хорошо — и даже достаточно для эвристического понимания того, как работает хи-вадрат, однако давайте все же посмотрим чуть глубже в то, что осталось под капотом.
9.3.1 Распределение \(\chi^2\)
Почему вообще критерий называется хи-квадрат? Откуда берется p-value? И куда делось «построение закона распределения статистики критерия при условии, что нулевая гипотеза верна»?
Обо всём по порядку. Еще раз вернемся к алгоритму:
Формулировка гипотезыВыбор статистического критерияВыбор уровня значимости \(\alpha\)- Построение закона распределения статистики критерия при условии, что нулевая гипотеза верна
- Расчёт выборочной статистики
- Расчёт достигнутого уровня значимости p-value
- Сопоставление \(\alpha\) и p-value и вынесение решения
Первые три пункта вычеркнуты — их мы обсудили. Гипотезу сформулировали, статистический критерий выбрали, уровень значимости оставили конвенциональным. Что дальше?
Статистика критерия — любого, не только \(\chi^2\) — это непрерывная случайная величина. И она подчинается некоторому распределению. В частности, статистика рассматриваемого нами критерия подчинается распределению \(\chi^2\), которое выглядит вот так:
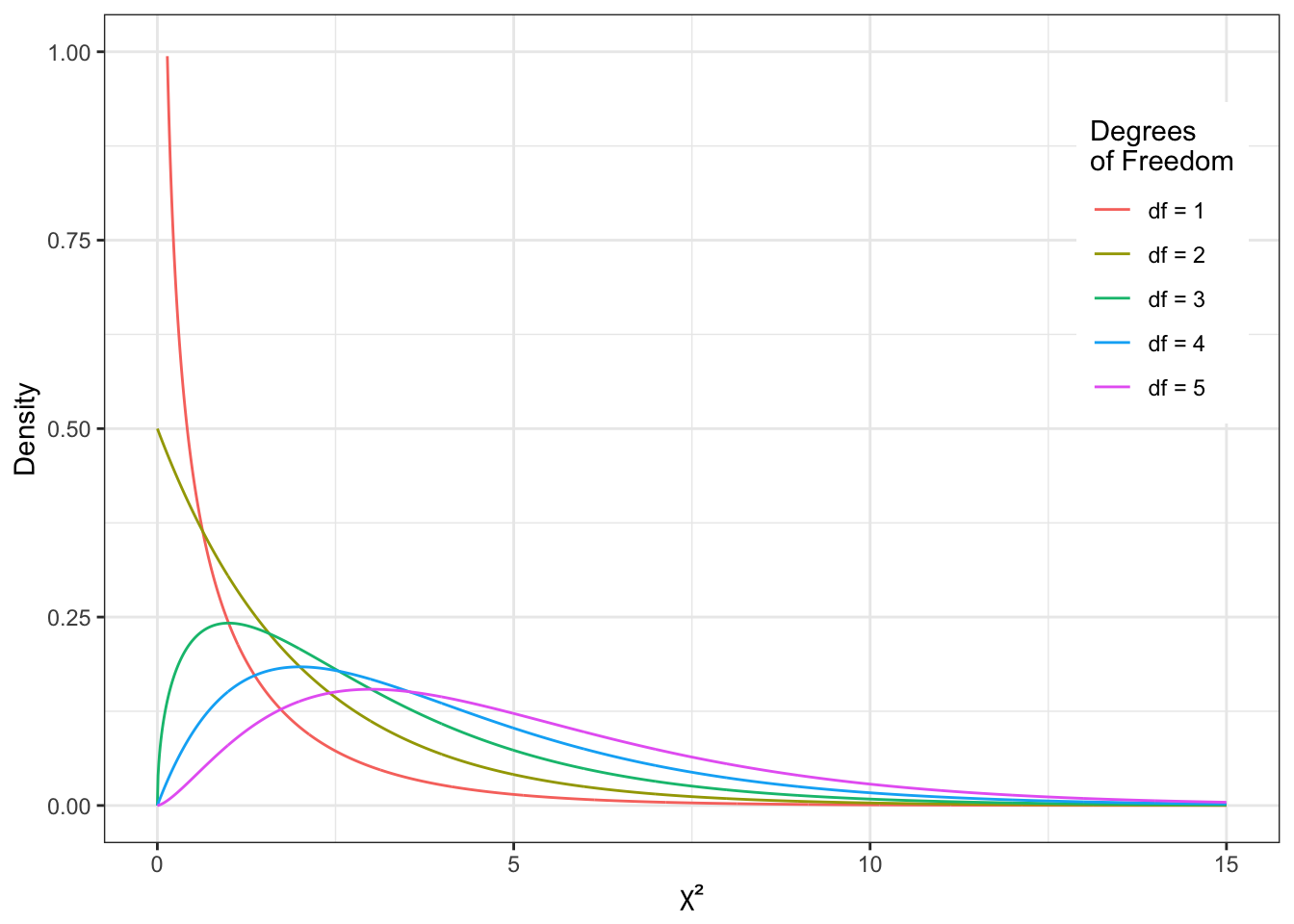
Важно: так выглядит распределение статистики \(\chi^2\) при условии, что нулевая гипотеза верна! Именно его мы и строим. Ну, как строим: оно уже построено за нас. Нам надо только понять, какое из возможных использовать. Мы видим, что форма распределения зависит от количества степеней свободы. Значит нам надо научиться рассчитывать количество степеней свободы для конкретного случая. Это делается так:
\[ \text{df} = (c−1)(r−1), \]
где \(c\) — количество столбцов в таблице сопряженности, \(r\) — количество строк в таблице сопряженности. В случае двух бинарных (дихотомических) переменных в таблице сопряженности два столбца и две строки — значит количество степеней свободы равно \(1\).
Итак, интересующее нас распределение — вот это:
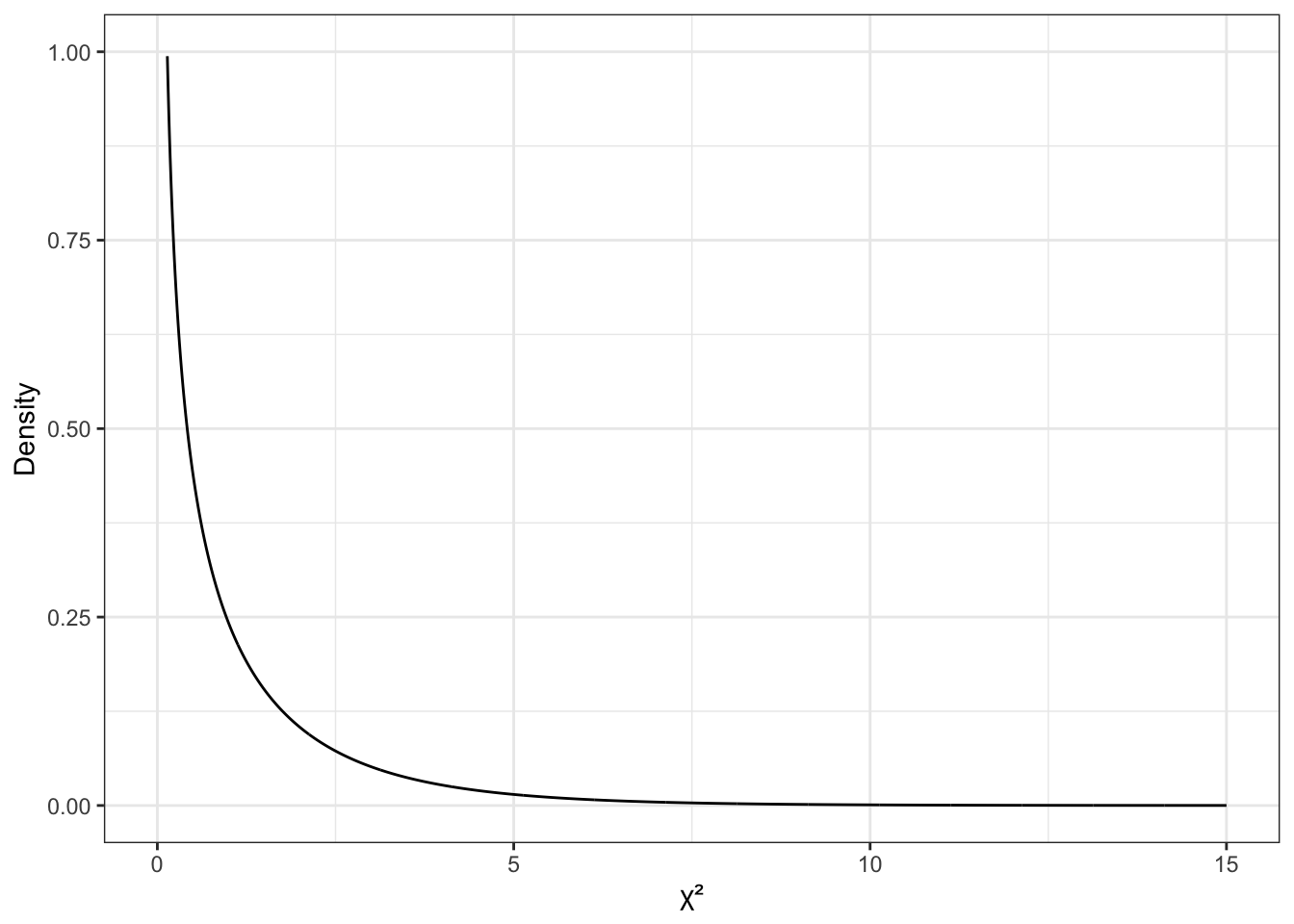
Как мы помним из темы про случайные величины, чем выше график плотности вероятности, тем чаще встречаются значения переменной. В данном случае мы видим, что при справедливости нулевой гипотезы малые значения \(\chi^2\) встречаются очень часто — то есть являются типичными. Большие же значения встречаются редко.
Отобразим выбранный уровень значимости (красная область в хвосте графика):
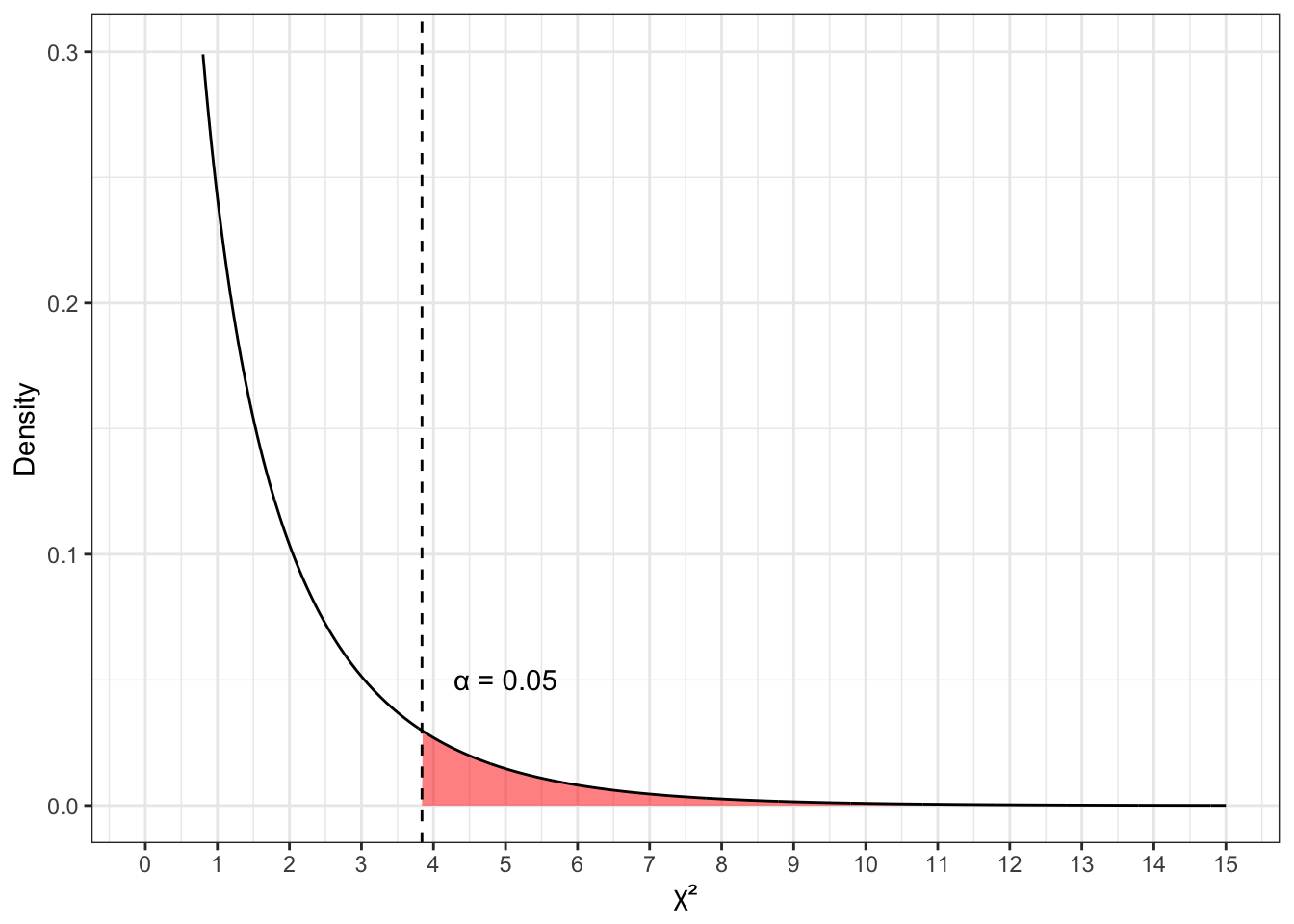
Мы немного ограничили ось \(y\) в пределах от 0 до 0.3, чтобы лучше видеть, что происходит — это связано с сильно асимметричной формой распределения. Красная область под графиком — это то, что называется критическая область, или область отклонения нулевой гипотезы.
Принципиально возможны две ситуации:
- рассчитанное значения \(\chi^2\) попало в критическую область
- рассчитанное значение \(\chi^2\) не попало в критическую область
Если случился первый вариант, то это выглядит так:
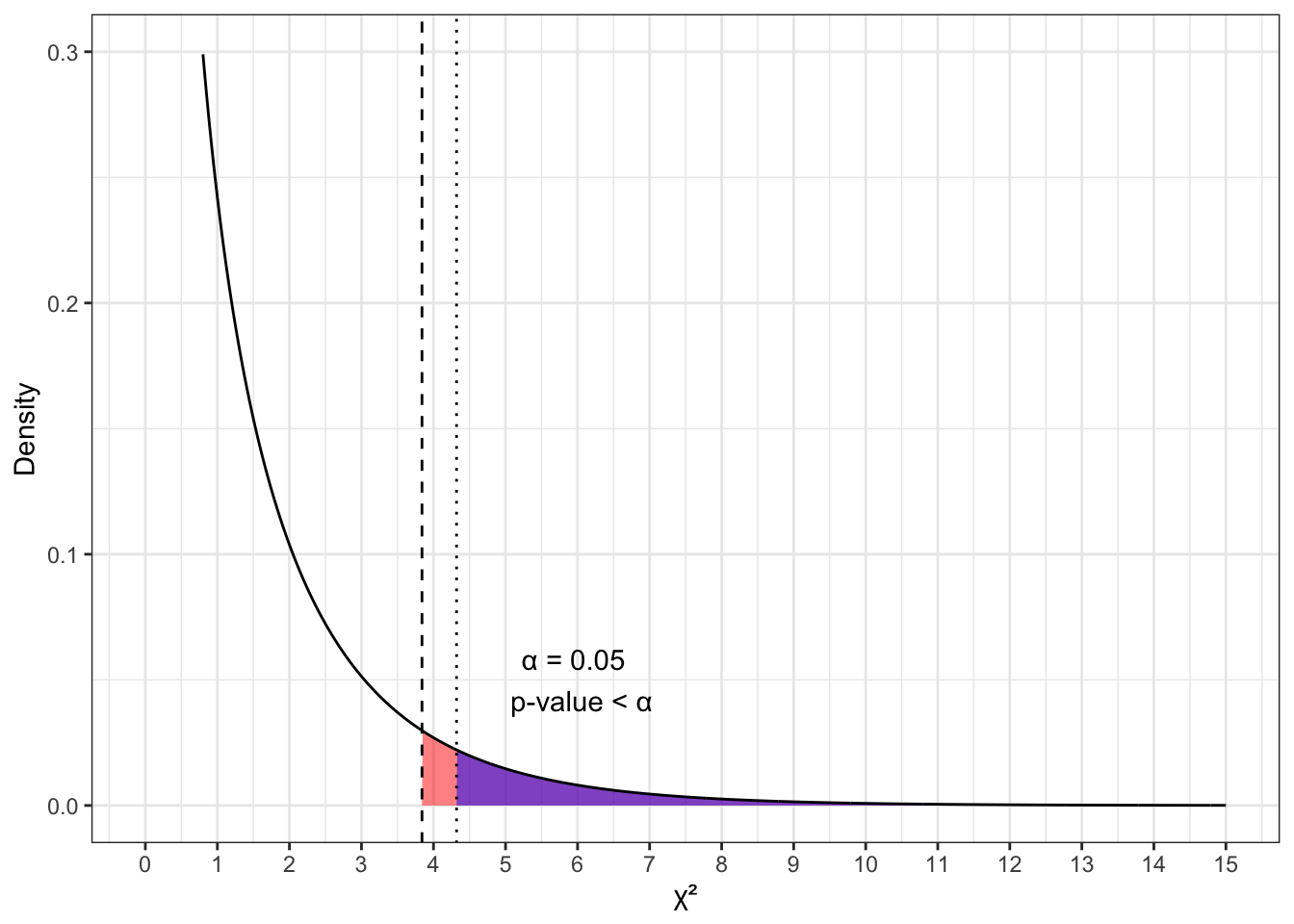
Геометрически p-value — это площадь под графиком распределения статистики при справедливости нулевой гипотезы правее от рассчитанного значения статистики. В терминах вероятности — это вероятность получить такие или более сильные отклонения при справедливости нулевой гипотезы. То есть, если p-value меньше \(\alpha\), то рассчитанное значение статистики попало в критическую область.
Если случился второй вариант, то это выглядит так:
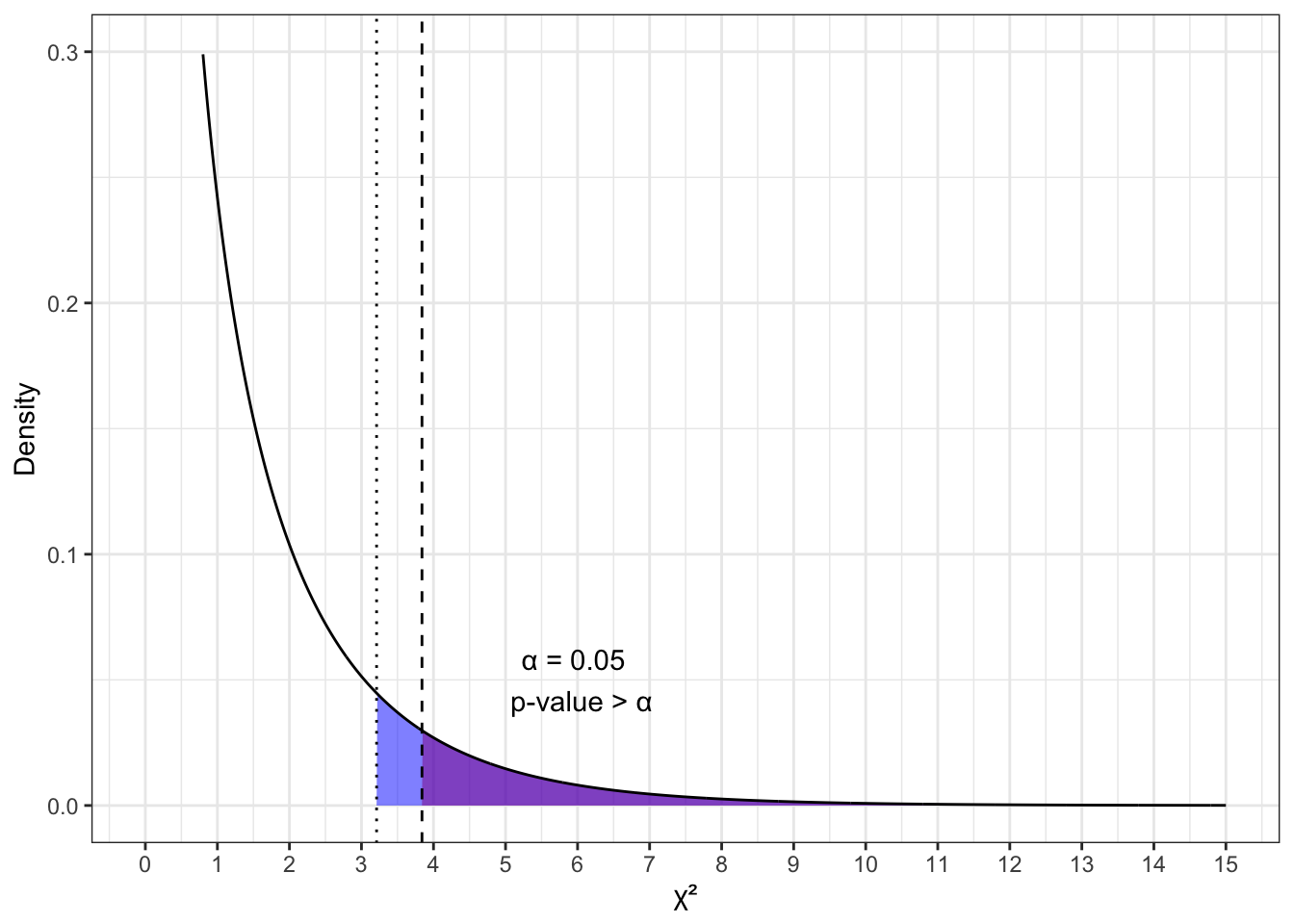
То есть, если p-value больше \(\alpha\), то рассчитанное значение статистики не попало в критическую область.
В этом смысле второй и первый сценарии тестирования статистической гипотезы, описанные в предыдущей главе, на самом деле две стороны одного и тогоже положения дел.
Итак,
- если мы получили p-value \(<\alpha\), то мы говорим, что
- мы получили значение статистики, не характерное для ситуации справедливости нулевой гипотезы,
- значит у нас есть основания отклонить нулевую гипотезу и принять альтернативную
- с надежностью вывода \(\alpha\), а точнее p-value.
- если мы получили p-value \(>\alpha\), то мы говорим, что
- мы получили значение статистики, характерное для ситуации справедливости нулевой гипотезы,
- значит у нас нет оснований отклонить нулевую гипотезу,
- надежность вывода в этом случае неизвестна.
Таким образом, в нашем случае p-value \(= 9.946 \cdot 10^{-14}\), что много меньше \(0.05\), что дает нам весовые основания отклонить нулевую гипотезу об отсутствии связи между подготовкой к экзамену и успешностью его сдачи и принять альтернативную гипотезу о том, что такая связь есть.
Вот мы и сделали статистический вывод. На практике. И даже на содержательный вопрос ответили. Ну, как же мы хороши!
9.4 Критерий согласия Пирсона
Кроме критерия независимости Пирсона, существует еще критерий согласия Пирсона. По сути, это некоторая вариации того, что мы изучили выше — и он даже проще, так как мы сравниваем эмпирические частоты с некоторыми заранее известными теоретическими. Собственно, поэтому он называется критерием согласия — согласовано ли наше эмпирическое распределение с некоторым заранее известным теоретическим.
Откуда мы знаем теоретические частоты? Ну, в общем случае — ниоткуда. Ведь это частоты генеральной совокупности, а о ней, как известно, ничего достоверно неизвестно. По этой причине любые критерии согласия в целом используются в исследовательской практике весьма редко. Обычно они являются частью какого-либо другого статистического метода — это мы увидим в следующей главе.
И все же исследовательскую задач для критерия согласия Пирсона придумать можно. Скажем, вы аппробируете психометрический опросник, и вам надо показать, что ваша выборка аппробации репрезентативна относительно генеральной совокупности в отношении распределения респондентов по полу. Генеральная совокупность — Российскаф Федерация. Где взять теоретические частоты — ведь мы не можем исходить из предположения, что доли мужчин и женщин в России одинаковы? Хвала небесам, у нас есть Росстат — он же Федеральная служба государственной статистики — который нам рассказал, что мужчин в РФ 46%, а женщин по несложным подсчетам — 54%.
Пусть мы собрали выборку в 495 человек, из которых 262 — мужчины, а 233 — женщины. Наша таблица эмпирических частот будет такой:
## f m
## 233 262Теоретические частоты будут таковы — рассчитываются по формуле \(p \cdot N\), где \(p\) — теоретическая доля, \(N\) — количество наблюдений:
| female | male |
|---|---|
| \(0.54 \cdot 495 = 267.3\) | \(0.46 \cdot 495 = 227.7\) |
Формула для расчета статистики критерия вот:
\[ \chi^2 = \sum_{i} \frac{(O_i-E_i)^2}{E_i}, \]
где \(O_i\) — эмпирические (наблюдаемые, observed) частоты, а \(E_i\) — теоретические (ожидаемые, expected) частоты.
На что-то очень похоже, да?
Степени свободы, так как строчка в таблице только одна, рассчитываются следующим образом:
\[ \text{df} = c - 1, \]
где \(c\) — число колонок в таблице.
- Нулевая гипотеза тут будет такая: эмпирические частоты равны теоретическим.
- Альтернативная гипотеза — эмпирические частоты отличаются от теоретических.
Статистический вывод абсолютно идентичен критерию независимости Пирсона.
Итого,
##
## Chi-squared test for given probabilities
##
## data: d_gender
## X-squared = 9.5682, df = 1, p-value = 0.00198Снова видим p-value \(< \alpha\), значит мы получили значение статистики, не характерное для ситуации справедливости нулевой гипотезы, и у нас есть основания отклонить нулевую гипотезу и принять альтернативную о том, что эмпирические частоты отличаются от теоретических.
Получается, что наша выборка не особо репрезентативна. Грустно… :(
Напоследок отметим, что если мы используем специально обученное ПО, мы вообще-то мало что делаем руками — только строчку кода пишем. Остальное же — формулирование гипотезы, построение распределения, подсчет статистики и p-value — за нас делает машина. Нам остается включить мозг, когда мы делаем статистический вывод.