12 Многофакторный дисперионный анализ

Окей, мы разобрались с одним фактором. А что делать если у нас несколько независимых переменных? Ну, раз есть однофакторный дисперсионный, значит должен быть и многофакторный! Попробуем разобраться.

12.1 Усложняем э-э-эксперимент

Итак, в предыдущем варианте мы изучали, как валентность стимула связана со скоростью его опознания на задаче лексического решения. Во-первых, давайте сделаем так, чтобы каждый испытуемый проходил все экспериментальные условия, и таким образом посмотрим на дисперсионный анализ с повторными измерениями (repeated measures ANOVA, rmANOVA). Во-вторых, кроме валентности — положительной, отрицательной и нейтральной — важной характеристикой стимула с точки зрения исследования эмоций является ещё и arousal — степень выраженности эмоции от стимула (обычно переводят как «возбуждение», хотя, кажется, «интенсивность» по смыслу ближе). Оба перевода так себе, поэтому будем использовать термин «эраузал» — такие мы модные, шо жесть просто. Пусть у нас есть стимулы с высоким эраузалом и с низким эраузалом. Итого, нам эксперимент будет выглядеть как-то так:

ЗП — время реакции
НП1 — валентность: три уровня — нейтральные, негативные, позитивные
НП2 — эраузал: два уровня — низкий и высокий

С точки зрения дисперсионного анализа у нас два фактора и одна зависимая переменная. Гениально.

Так, стоп — если у нас два фактора, можно ли провести два однофакторных анализа и успокоиться?

Можно. Нужно ли так делать?

Не нужно.

12.2 Взаимодействие факторов

Дело в том, что нам надо осмыслять картину происходящего как целое — во славу гештальта! — так как факторы могут взаимодействовать друг с другом. Получается, что в случае многофакторного дисперсионного анализа у нас появляются два эффекта:

основной эффект фактора — интерпретируется аналогично тому, как это делалось в однофакторном дисперсионном анализе
эффект взаимодействия факторов — говорит нам о том, что влияние одного фактора на зависимую переменную различается на разных уровнях другого фактора.

Посмотрим на картинки. Пусть есть два фактора A и B и какая-то зависимая переменная. Возможны следующие ситуации:

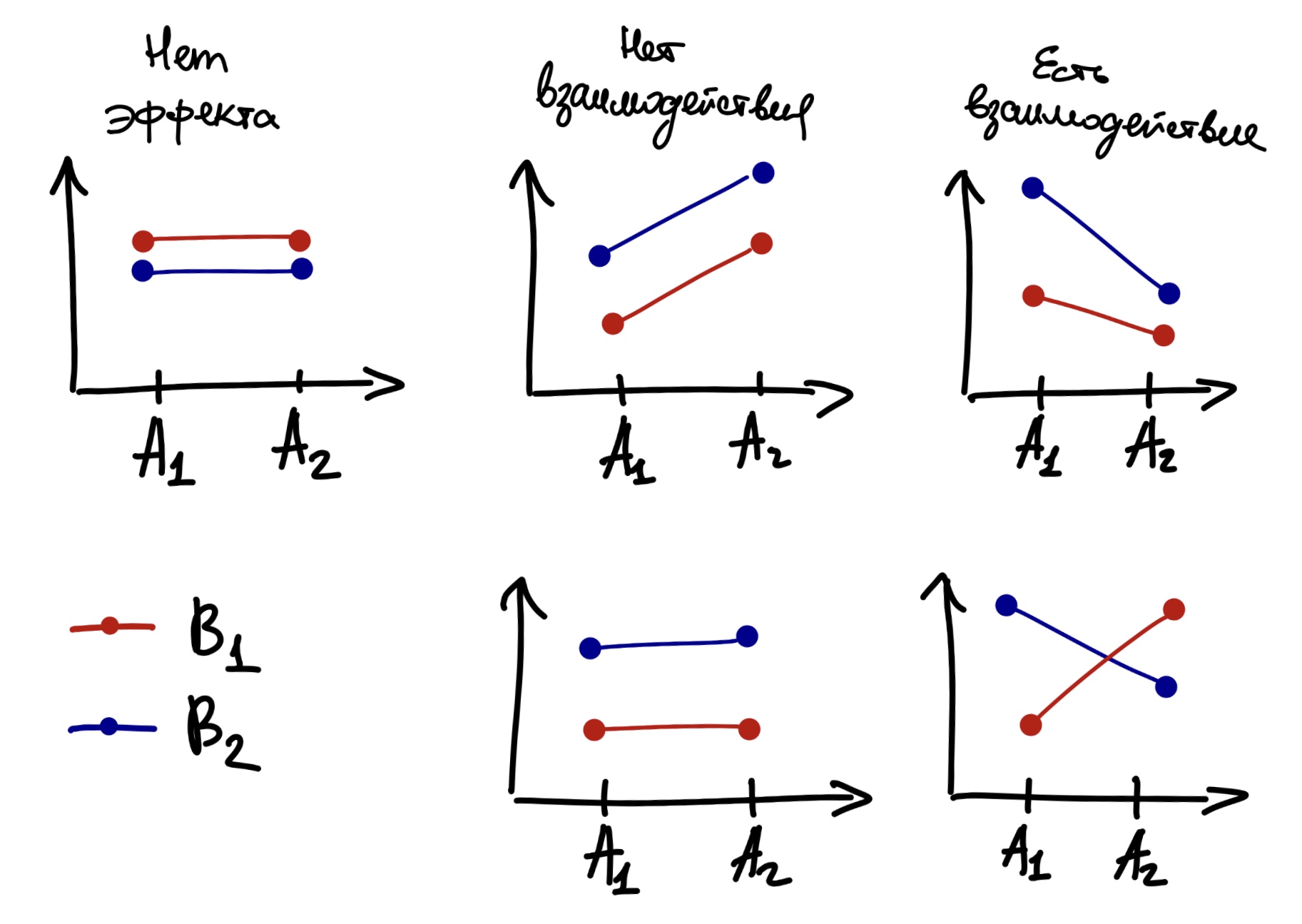
Вообще значимое взаимодействие факторов — это двоякая штука. С одной стороны, мы обнаружили интересную закономерность — возможно, именно ту, которую искали, и c’est cool. С другой стороны, взаимодействие,

во-первых, может маскировать главные эффекты — если мы смотрим только на главные эффекты, то теряем часть информации о закономерности
во-вторых, и это связано с первым пунктом, оно затрудняет интерпретацию основных эффектов.

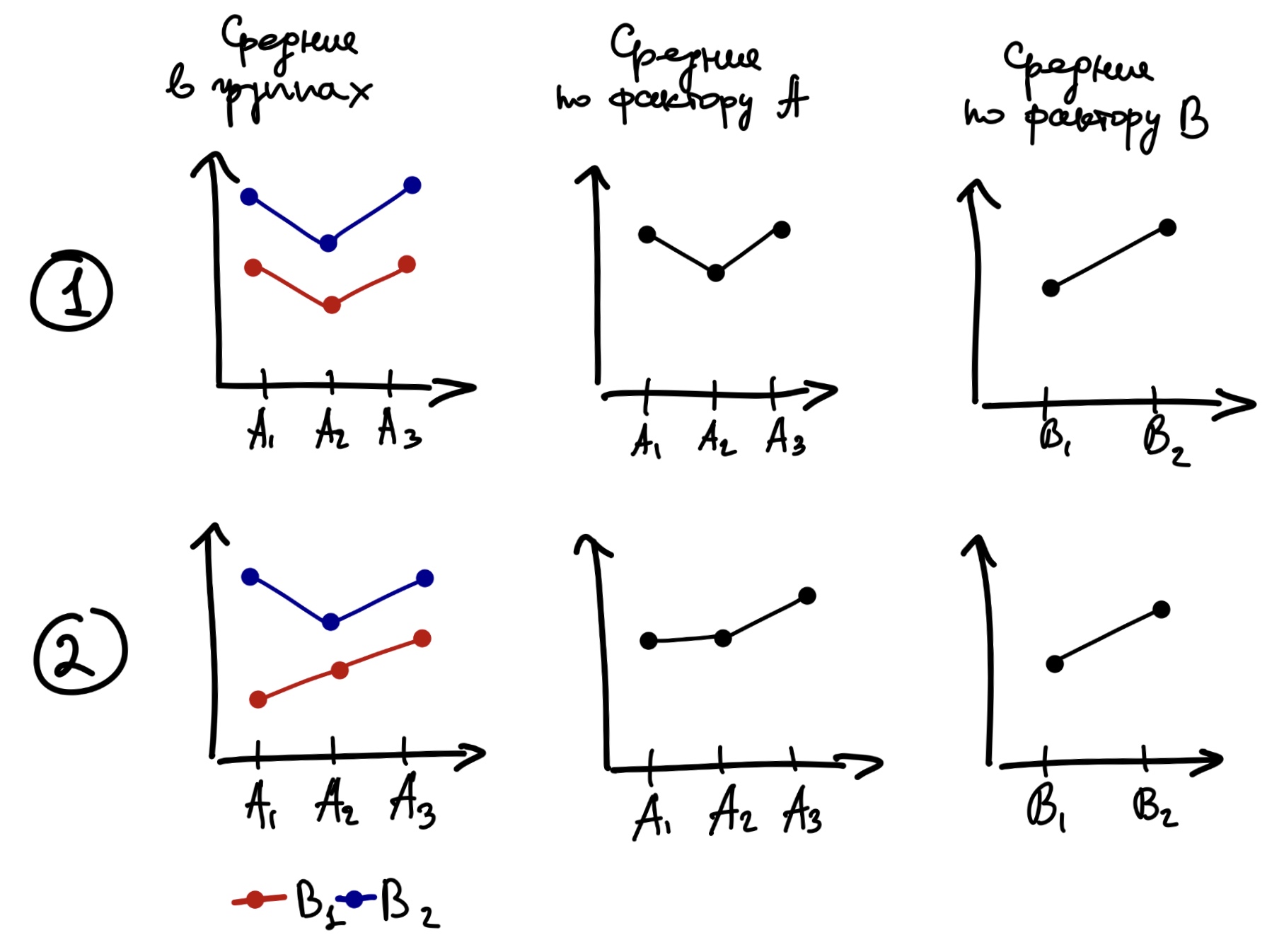
Если взаимодействие не значимо, то с интерпретацией главных эффектов трудностей не возникает. Если взаимодействие значимо, то обсуждать главнные эффекты необходимо аккуратно, или не обсуждать вовсе. В частности, нижний ряд рисунков выше показывает, как эффект фактора A частично маскирует эффект фактора B, что отражается во взаимодействии.

Конечно, в модель можно ввести и более двух факторов, и логика тестирования статистической значимости останется, как и всегда, та же самая. Но помните, что чем сложнее модель, тем сложнее её интерпретация. А интерпретируя взаимодействие трёх предикторов вовсе можно сойти с ума.

В связи с этим, есть следующий момент. Когда вы планируете ваше исследование, сразу подумайте, как вы будете анализировать данные — что будет входить в модель в качестве основных предикторов, что в качестве ковариат, и какие взаимодействия в ней будут. Иначе измерить кучу переменных вы построите модель, результаты которой невозможно будет понять. Дизайн исследования очень тесно связан с аналитикой.

12.3 Результаты многофакторного дисперсионного анализа и тестирование значимости факторов и взаимодействий

Таблица результатов многофакторного анализа невероятно похожа на то, что было в однофакторном анализе, только строк чуть побольше, потому что факторов побольше:

## $ANOVA
##            Effect DFn DFd         F            p p<.05         ges
## 2         valency   2 118 12.416635 1.276747e-05     * 0.064098306
## 3         arousal   1  59  2.873217 9.533691e-02       0.008412731
## 4 valency:arousal   2 118  4.742011 1.045078e-02     * 0.028560826
## 
## $`Mauchly's Test for Sphericity`
##            Effect         W         p p<.05
## 2         valency 0.9829358 0.6070562      
## 4 valency:arousal 0.9420687 0.1771719      
## 
## $`Sphericity Corrections`
##            Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF]
## 2         valency 0.9832221 1.467099e-05         * 1.0168281 1.276747e-05
## 4 valency:arousal 0.9452410 1.186789e-02         * 0.9755722 1.106044e-02
##   p[HF]<.05
## 2         *
## 4         *

Мы видим знакомую нам таблицу результатов дисперсионного анализа, где есть F-стастика и p-value. Статистический вывод осуществляется так же, как и обычно. В данном случае мы видим, что фактор валентности стистически значим, как и в предыдущем анализе, фактор эраузала — не значим, а вот их взаимодействие значимо. Ну, давайте нарисуем картинку, чтобы попытаться понять, что происходит.

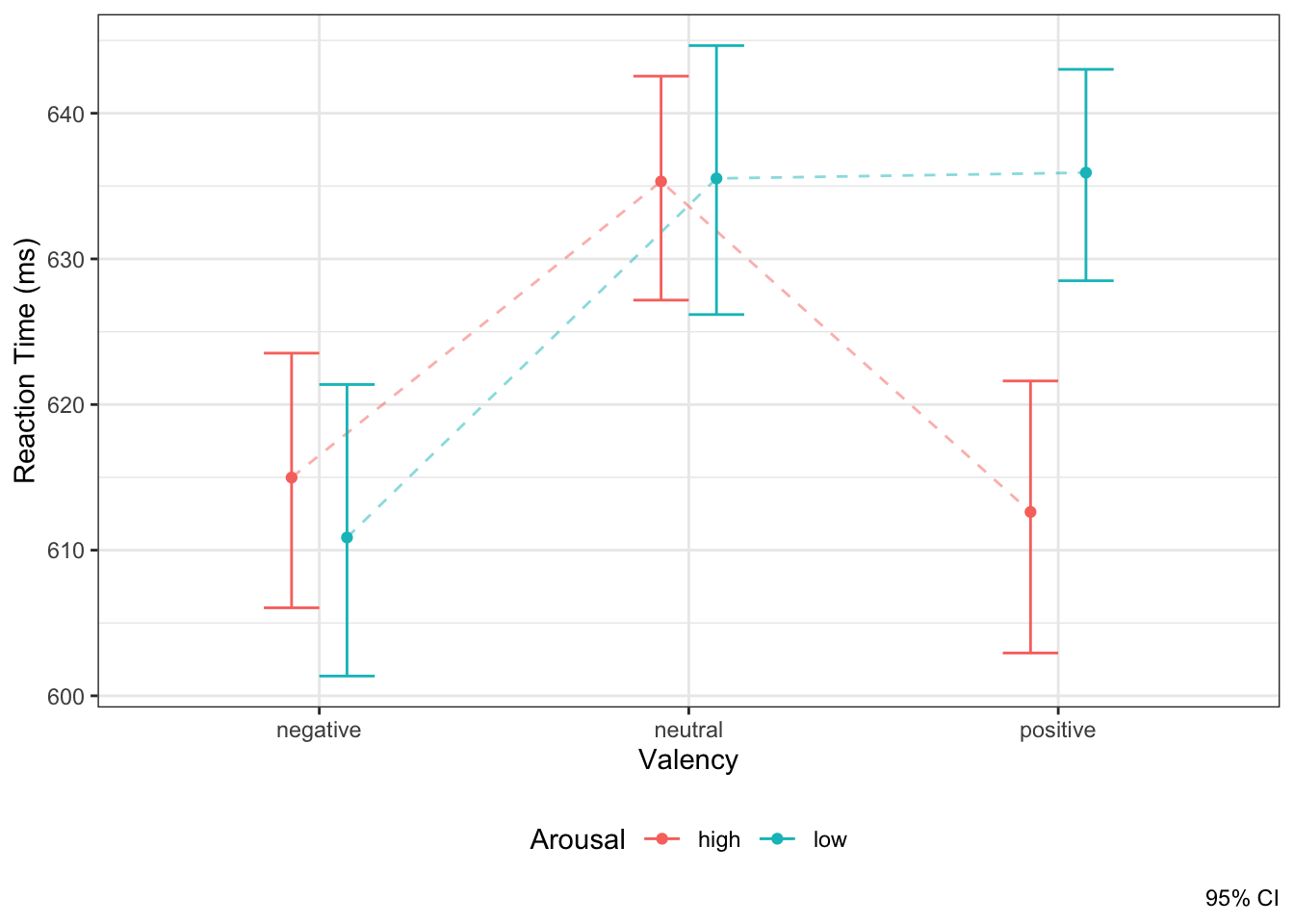
Ну, вот как-то так — явственно явлено взаимодействие предикторов.

12.4 Условия применения дисперсионного анализа с повторными измерениям

Здесь их меньше, потому что допущения о независимости наблюдений между группами, очевидно, не выполнено.

Количественная непрерывная зависимая переменная
Нормальное распределение признака в статистических совокупностях, из которых извлечены выборки.
Сферичность данных
- Проверяется с помощью теста Моучли (Mauchly test)

12.4.1 Сферичность

Как можно заметить, в списке нет допущения об гомогенности дисперсий — ведь у нас одна выборка, с которой мы получаем несколько измерений. В случае дисперсионного анализа с повторными измерениями проверяется предположение о сферичности данных (sphericity).

Сферичность — это модель данных, согласно которой дисперсии разностей между всеми парами уровней фактора равны. Нарушение допущение о сферичности — то есть отсутствие равенства дисперсий между парами уровней фактора — является серьезной проблемой для rmANOVA, так как при этом тест становится слишком либеральным, то есть увеличение вероятность ошибки I рода.

К нашему счастью, если есть нарушение сферичности данных, то машина сама нам об этом сообщит, а также применит необходимые поправки, чтобы избежать рост вероятности ошибки I рода. Формулы смотреть не будет, потому что их все равно никто не знает.

12.5 Типы сумм квадратов

Когда у нас в анализе появляется несколько факторов, мы можем тестировать их значимость различными способами. Способ тестирования определяет типа сумм квадратов, которых существует три.

Первый (I) тип сумм квадратов проводит последовательные тесты значимости факторов. Величина эффекта фактора зависит от объёма выборки. Кроме того, результат вычислений зависит от порядка включения факторов в модель, что не оч хор.
Второй (II) тип сумм квадратов проводит иерархические тесты, поэтому в этом случае результаты не зависят от порядка включения факторов в модель, однако величина эффекта все ещё зависит от объема выборки.
Третий (III) тип сумм квадратов проводит частные тесты. К данному подходу есть некоторые статистические вопросы, однако результаты в этом случае не зависят ни от порядка включения факторов в модель, ни от объёма выборки. По этой причине данный тип используют в случае несбалансированных данных, когда объемы групп по факторам различаются.

Вероятно, и это вполне нормально, что про суммы квадратов сейчас ничего не понятно. Это ожидаемо и приемлемо, поскольку там надо немного глубоко копнуть в происходящее. Сейчас надо запомнить вот что:

Если у нас экспериментальный дизайн исследования, то мы, во-первых, на уровне планирования исследования делаем всё возможное, чтобы группы были уравнены, а также у нас, как правило, есть возможность добрать испытуемых, если в какой-то из групп из не хватает. Тогда мы по умолчанию используем II тип суммы квадратов.
Если же у нас опросниковое исследование или такой дизайн, где респонденты разбиваются на группы post factum, мы не можем гарантировать, что эти группы окажутся равными по численности. В этом случае нам может помочь III типа суммы квадратов.