1 L1 // Основы R. Типы и структура данных. Функции и управляющие конструкции

1.1 Установка R и RStudio

Чтобы стать счастливым пользователем R, надо установить на свой комп две программы:

собственно R
- на Win
- на Mac
- на Linux
IDE RStudio ¹

Причем во избежание возможных проблем, надо поставить программы именно в этом порядке — сначала R, а потом RStudio, иначе IDE может на найти R и будет ругаться.

1.2 R как язык программирования. Команды

В R нет команд и практически нет ключевых слов, распространенных в других языках программирования. Практически все операции обернуты в функции. Остаются только математические и логические операторы, которые, на самом деле, тоже функции.

1.2.1 Математические операции

Все в наличии:

2 + 3 # сложение

[1] 5

4 - 1 # вычитание

[1] 3

5 * 12 # умножение

[1] 60

5 ^ 8 # возведение в степень

[1] 390625

4 / 7 # деление

[1] 0.5714286

5 %/% 3 # целочисленное деление

[1] 1

5 %% 3 # остаток от деления

[1] 2

Скобки также существуют и привычно работают:

6 / 3 + 2 * 4

[1] 10

6 / (3 + 2) * 4

[1] 4.8

6 / ((3 + 2) * 4)

[1] 0.3

1.2.2 Математические функции

Можно посчитать корень:

sqrt(16)

[1] 4

Или логарифм:

log(10)

[1] 2.302585

log(8, base = 2)

[1] 3

log(8, 2)

[1] 3

Или что-то на тригонометрическом:

sin(5); cos(5); tan(5)

[1] -0.9589243

[1] 0.2836622

[1] -3.380515

Кстати, можно и вот так — это к тому, что математические операторы тоже являются функциями:

`+`(2, 3)

[1] 5

`^`(4, 5)

[1] 1024

`/`(8, 3)

[1] 2.666667

1.2.3 Логические операции

К логическим операциями можно отнести операции сравнения:

5 > 4 # больше

[1] TRUE

6 < 2 # меньше

[1] FALSE

5 >= 5 # больше или равно

[1] TRUE

6 <= 3 # меньше или равно

[1] FALSE

23 == 14 # равно

[1] FALSE

77 != 98 # не равно

[1] TRUE

А также логические операторы И (&) и ИЛИ (|):

TRUE & TRUE

[1] TRUE

TRUE & FALSE

[1] FALSE

FALSE & FALSE

[1] FALSE

TRUE | TRUE

[1] TRUE

TRUE | FALSE

[1] TRUE

FALSE | FALSE

[1] FALSE

1.2.4 Переменные и объекты

Результаты вычислений и преобразований хотелось бы сохранять, поэтому в R существует оператор присваивания <-:

x <- 5
y <- 4 * 8

Можно, конечно, написать и x = 5, но сообщество вас не поймет и будет косо смотреть… Когда мы присвоим некоторой переменной какой-либо объект, он отобразиться в окошке Environment, и с ним можно будет работать. Например, совершать разные операции:

x + y

[1] 37

sqrt(x)

[1] 2.236068

log(y, base = x)

[1] 2.153383

Объектом в R может быть вообще все, что угодно — число, строка, вектор, матрица, датафрейм, таблица, результат моделирования, функция и т.д.

1.3 Типы данных

Тип данных — это характеристика данных, которая определяет:

множество допустимых значений, которые могут принимать данные этого типа
допустимые операции над данными этого типа

1.3.1 `numeric`

Это числа с десятичной частью.

class(3.14)

[1] "numeric"

typeof(3.14)

[1] "double"

"double" нам говорит о том, что числа с десятичной частью храняться в R с двойной точностью. И это хорошо.

1.3.2 `integer`

Это целые числа.

class(3)

[1] "numeric"

Правда чтобы создать именно целое число, надо указать, что мы хотим именно целое число с помощью литерала L:

class(3L)

[1] "integer"

typeof(3L)

[1] "integer"

По умолчанию объект типа 3 воспринимается R как 3.0, поэтому тип данных будет numeric.

1.3.3 `complex`

Комплексные числа тоже существуют, и мы с ними немного познакомимся, чтобы перестать их бояться.

class(2+3i)

[1] "complex"

1.3.4 `character`

Текст тоже надо как-то хранить.

s1 <- 'a'
s2 <- "это строка"

class(s1)

[1] "character"

class(s2)

[1] "character"

Кавычки не важны, если у вас не встречаются кавычки внутри кавычек. Тогда надо использовать разные:

s <- 'Мужчина громко зашёл в комнату и высказал решительное "здравствуйте"'
s

[1] "Мужчина громко зашёл в комнату и высказал решительное \"здравствуйте\""

1.3.5 `factor`

Бывают такие переменные, которые группируют наши данные. Например,

город проживания (Москва, Санкт-Петербург, Казань, Екатеринбург)
уровень образования (бакалавриат, специалитет, магистратура, аспирантура)
экспериментальная группа (group1, group2, control)
и др.

Обычно они текстовые. Для них был придуман тип данных factor, чтобы их было дешевле хранить. Однако большинство современных пакетов сами могут решить, когда надо текст перевести в фактор.

Ordered factor (упорядоченный фактор) — тип данных, который позволяет задать порядок групп. Например,

уровень образования: bachelor < master < phd < postdoc
сложность экспериментальной задачи: easy < medium < hard
и др.

Вот упорядоченный фактор нам время от времени может понадобиться — например, для создания визуалиация или в некоторых статистических моделях.

1.3.6 Специальные литералы

1.3.6.1 `NA`

Пропущенное значение (Not Available). Обозначает отсутствие значения там, где оно вроде бы должно быть. Причины могут быть разные:

технические ошибки записи данных
ошибки настройки платформы — забыли сделать ответы обязательными
организация исследования — ограничили время на ответ
«честный» пропуск — дали возможность не отвечать на вопрос
предобработка данных — специально создали NA, чтобы далее с ними работать
и др.

1.3.6.2 `NaN`

Это не число (Not a Number).

0 / 0

[1] NaN

1.3.6.3 `NULL`

Это ничто. Пустота. Используется для задания аргументов функций.

ggplot(data = NULL)

1.4 Структуры данных

Структура данных — это способ и форма объединения однотипных и/или логически связанных данных.

1.4.1 Датафрейм

Воплощение привычной нам «таблицы» в R.

# A tibble: 6 × 10
  carat cut       color clarity depth table price     x     y     z
  <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48

Это сложная структура данных. Чтобы понять всю её мощь, необходимо начать с более простых.

1.4.2 Векторы

Вектор — это набор чисел.

\[ \pmatrix{1 & 4 & 36 & -8 & 90.1 & -14.5} \]

Если это утверждение вызывает у вас внутренний протест, давай проследим пусть от направленного отрезка в набору чисел.

Возьмем направленный отрезок — вектор:

Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'

Именно так мы понимали вектор в школе. Договоримся, что все векторы у нас начинаются из точки \((0, 0)\):

Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'

Если теперь у нас все вектора начинаются из начал координат, то мы можем полностью описать вектор только координатами его конца. Поэтому уберем вектор:

Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'

То есть для нас теперь вектор равносилен точке на плоскости. А точка однозначно описывается двумя координатами. Получается, можно просто записать:

\[ \pmatrix{1 & 2} \]

Получается, что это одно и то же:

\[ \pmatrix{1 & 0.5}, \quad \pmatrix{2 & 3}, \quad \pmatrix{4.2 & -3.5} \]

Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'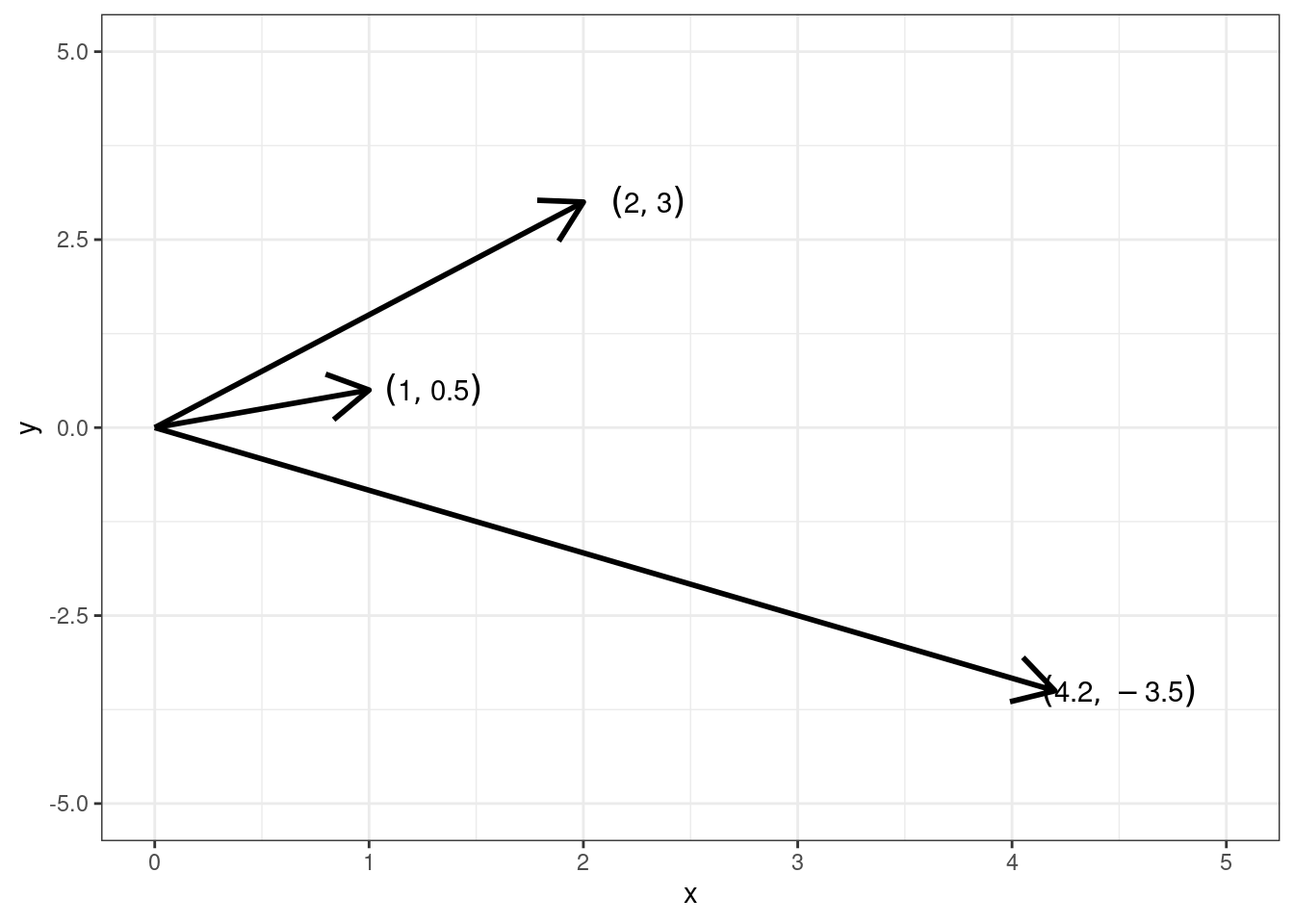

Теперь обобщим вектор на более общие случаи:

Вектор — это набор некоторого колчиества элементов одного типа.

v_num <- c(1, 6, -34, 7.7) # числовой вектор
v_char <- c("Москва", "Санкт-Петербург", "Нижний Новгород", "Пермь") # текстовый вектор
v_log <- c(TRUE, FALSE, TRUE, TRUE) # логический вектор

class(v_num)

[1] "numeric"

v_num

[1]   1.0   6.0 -34.0   7.7

class(v_char)

[1] "character"

v_char

[1] "Москва"          "Санкт-Петербург" "Нижний Новгород" "Пермь"

class(v_log)

[1] "logical"

v_log

[1]  TRUE FALSE  TRUE  TRUE

1.4.2.1 Индексация векторов

Из вектора можно вытащить его элемент:

v_char[2] # по номеру

[1] "Санкт-Петербург"

v_num[v_num > 5] # по условию

[1] 6.0 7.7

1.4.2.2 Векторизация

Для того, чтобы выполнить операцию на всем векторе поэлементно, не нужно перебирать его элементы.

vec <- 1:4
vec - 1

[1] 0 1 2 3

vec^2

[1]  1  4  9 16

sqrt(vec)

[1] 1.000000 1.414214 1.732051 2.000000

1.4.2.3 Recycling

Если мы будем, например, складывать два вектора разной длины, то более короткий зациклится.

vec1 <- 1:10
vec2 <- 1:2

vec1

 [1]  1  2  3  4  5  6  7  8  9 10

vec2

[1] 1 2

vec1 + vec2

 [1]  2  4  4  6  6  8  8 10 10 12

1.5 Матрицы

Если мы желаем приблизиться к датафрейму, то одного ряда элементов нам недостаточно — надо выходить во второе измерение! Поэтому уложим вектор в матрицу:

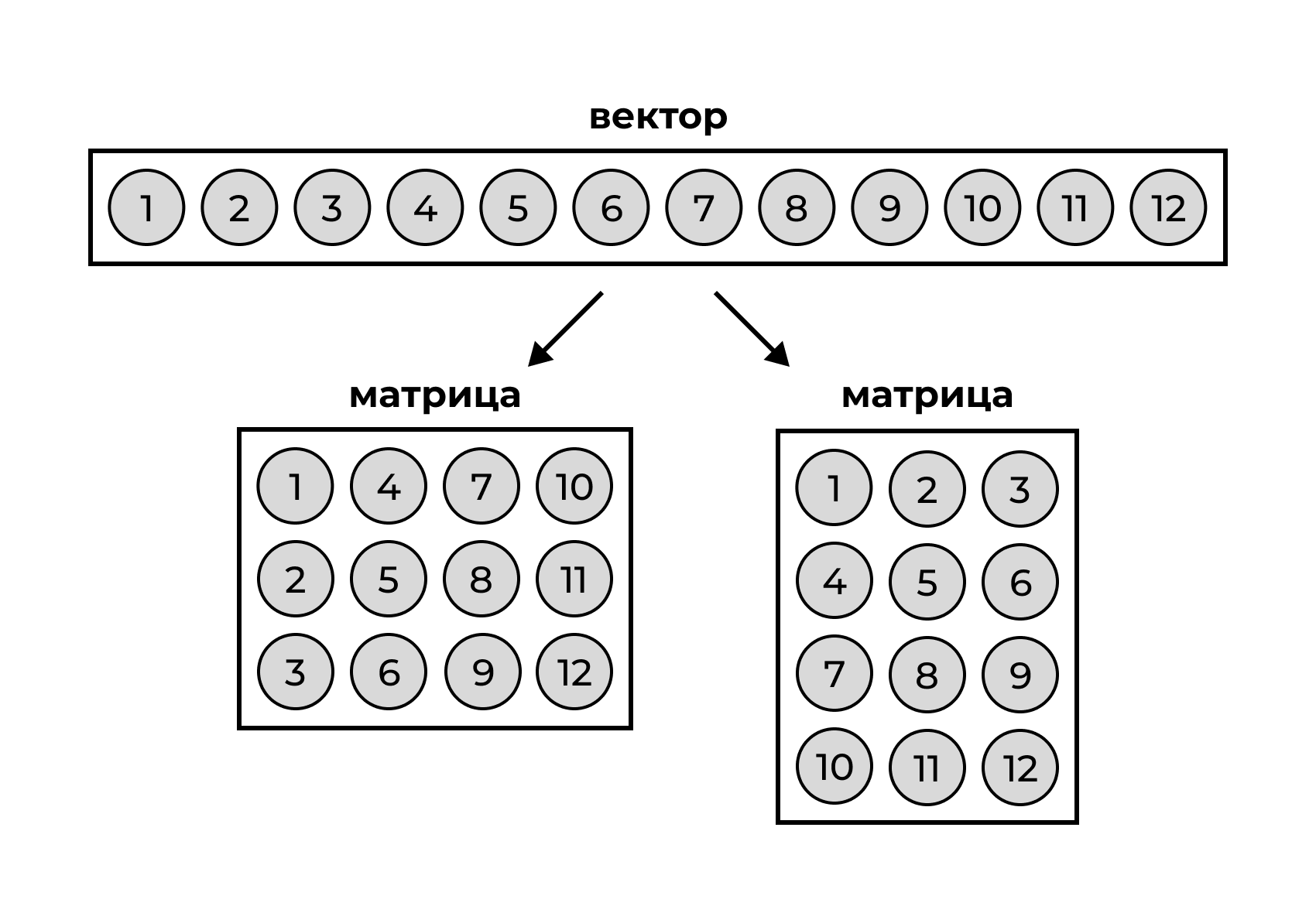
Варианты преобразования вектора в матрицу

Или вот еще разные варианты:

v <- 1:12
m1 <- matrix(v, nrow = 3)
m1

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

m2 <- matrix(v, nrow = 4)
m2

     [,1] [,2] [,3]
[1,]    1    5    9
[2,]    2    6   10
[3,]    3    7   11
[4,]    4    8   12

m3 <- matrix(v, nrow = 3, byrow = TRUE)
m3

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12

m4 <- matrix(v, nrow = 4, byrow = TRUE)
m4

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12

1.5.1 Индексация матриц

Из матрицы можно вытащить её элементы:

m1

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

m1[2, 3] # отдельный элемент

[1] 8

m1[1, ] # целую строку

[1]  1  4  7 10

m1[, 4] # целый столбец

[1] 10 11 12

m1[1:2, 2:4] # часть матрицы

     [,1] [,2] [,3]
[1,]    4    7   10
[2,]    5    8   11

1.6 Массивы

Вектор — одномерный массив.
Матрица — двумерный массив.
Массивы — структуры, которые объединяют данные только одного типа.

c(2, TRUE)

[1] 2 1

c(2, TRUE, "word")

[1] "2"    "TRUE" "word"

При объединении разных типов данных в одном массиве происходит приведение типов (coercion) по следующей иерархии:

logical → integer → numeric → complex → character

Это нам осложняет жизнь, так как мы бы хотели объединять данные разных типов в одну структуру.

1.7 Списки

Списки позволяют объединять массивы различных типов данных, чем делают нашу жизнь значительно приятнее.

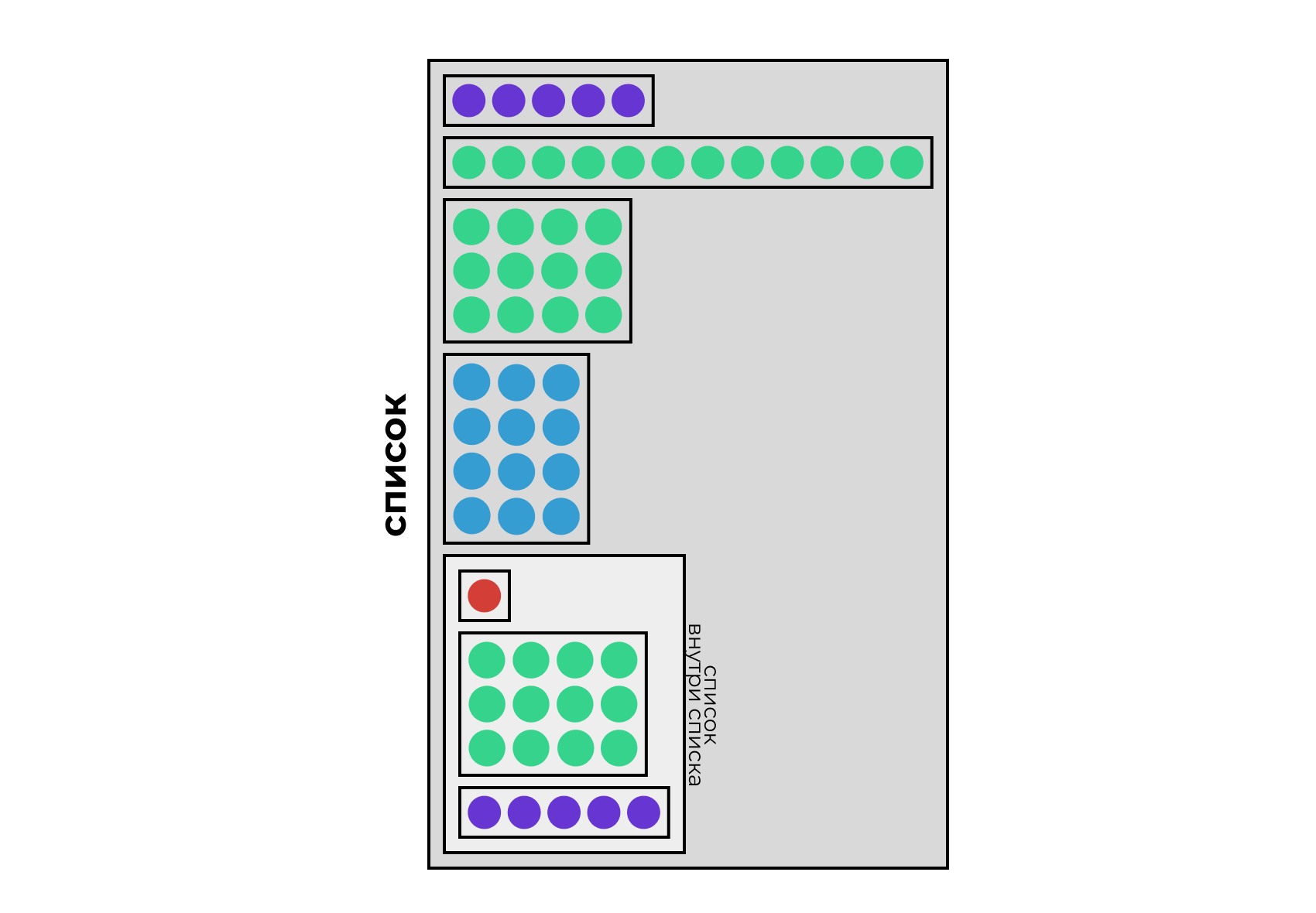
Например, так:

l <- list(v1 = v_num,
          v2 = v_char,
          m1 = m1,
          ls = list(v = v,
                    m = m3))
l

$v1
[1]   1.0   6.0 -34.0   7.7

$v2
[1] "Москва"          "Санкт-Петербург" "Нижний Новгород" "Пермь"          

$m1
     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

$ls
$ls$v
 [1]  1  2  3  4  5  6  7  8  9 10 11 12

$ls$m
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12

1.7.1 Индексация списков

l[1] # по номеру элемента, возвращается список

$v1
[1]   1.0   6.0 -34.0   7.7

l[[1]] # по номеру элемента, возвращается массив

[1]   1.0   6.0 -34.0   7.7

l$ls # по названию элемента

$v
 [1]  1  2  3  4  5  6  7  8  9 10 11 12

$m
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12

l$ls$m # можно идти многоуровнево

     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12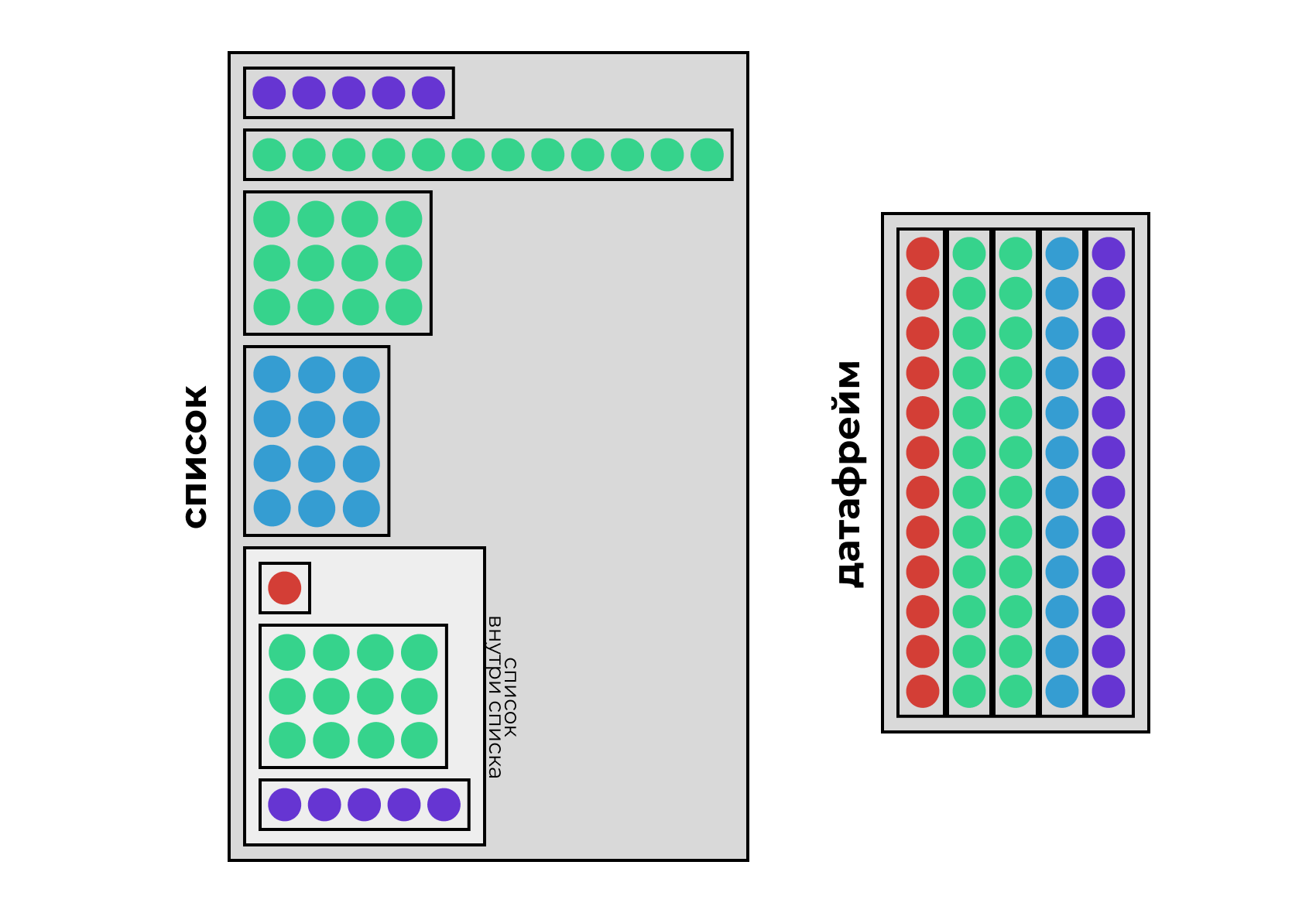

1.8 Собираем датафрейм

возьмем список
потребуем, чтобы его элементами были векторы
потребуем, чтобы эти векторы были одинаковой длины
расположим их «вертикально»

1.8.1 Индексация датафрейма

Для примера возьмем датафрейм про бриллианты:

diam

# A tibble: 6 × 10
  carat cut       color clarity depth table price     x     y     z
  <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48

Датафрейм наследует свойства списка и матрицы, что делает его невероятно гибким в обращении и крайне удобным в работе:

diam$carat # вытащить столбец

[1] 0.23 0.21 0.23 0.29 0.31 0.24

diam[diam$price > 330, ] # отобрать строки по условию

# A tibble: 3 × 10
  carat cut       color clarity depth table price     x     y     z
  <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
2  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
3  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48

diam[, c(2:3, 7)] # вытащить столбцы по номерам

# A tibble: 6 × 3
  cut       color price
  <ord>     <ord> <int>
1 Ideal     E       326
2 Premium   E       326
3 Good      E       327
4 Premium   I       334
5 Good      J       335
6 Very Good J       336

diam[1:4, c("carat", "price")] # вытащить отдельные строки по номерам и столбцы по названиям

# A tibble: 4 × 2
  carat price
  <dbl> <int>
1  0.23   326
2  0.21   326
3  0.23   327
4  0.29   334

1.9 Функции

Если какой-либо кусок кода повторяется более трех раз, имеет смысл обернуть его в функцию.

Как стоит понимать функцию?

Функция — это некий черный ящик, который

принимает что-либо на вход
проделывает с этим какие-либо операции
и что-то возвращает

1.9.1 Синтаксис функции

Синтаксис создания функции выглядит так:

function_name <- function(arguments) {
    ...
    body
    ...
    return()
}

Элементы функции:

имя функции (function_name) — как мы к ней будем обращаться при вызове
аргументы функции (arguments) — какие значения и объекты она принимает на вход
тело функции (body) — что она делает с входными объектами
возвращаемое значение (return()) — что функция вернет в качестве результата работы

Вызов функции:

function_name(arguments)

1.9.2 Пример функции

cot <- function(x) {
  result <- 1 / tan(x)
  return(result)
}
cot(3)

[1] -7.015253

Если функция простая, можно не создавать временные объекты:

cot <- function(x) {
  return(1 / tan(x))
}
cot(3)

[1] -7.015253

Если функция короткая, можно даже не писать return():

cot <- function(x) {
  1 / tan(x)
}
cot(3)

[1] -7.015253

1.9.3 Пример более полезной функции

Осторожно, большое!

Это функция, которая занималась предобработкой данных в реальном проекте. Прикиньте, если бы мы такой кусок кода повторяли для каждого датасета… — жуть!

Важно!

Вам не нужно сейчас подробно понимать, что написано ниже — мы все разберем по ходу курса и научимся писать такое же! Сейчас главное ухватить структуру функции — где аргументы, где тело, где возвращаемое значение. Всё! Остальное освоим по ходу дела.

mr_preproc <- function(d) {

  require(tidyverse)
  
  d |> select(
    # select columns we need
    "Индивидуальный_код",
    correctAns,
    base_pic,
    rotated_pic,
    resp_MR_easy.keys,
    resp_MR_easy.corr,
    resp_MR_easy.rt
  ) |>
    drop_na() |> # remove technical NAs (recording artefacts, not missing data)
    mutate(task = "MR",
           # add task name (mental rotation)
           level = "easy",
           # add difficulty level
           trial = 1:16) |> # number trials
    rename(
      "id" = "Индивидуальный_код",
      # rename columns for handy usage
      "key" = resp_MR_easy.keys,
      "is_correct" = resp_MR_easy.corr,
      "rt" = resp_MR_easy.rt
    ) -> MR # ready to use
  
  return(MR)
 
}

1.10 Условный оператор

Иногда при написании функции может понадобиться обработать какие-то важные случаи.

Например, в двух запусках сбора данных столбцы были названы по-разному: если это не учесть, код будет ломаться.

Для этого подойдет условный оператор.

1.10.1 Структура условного оператора

if (condition) {
  ...
  body
  ...
} else {
  ...
  body
  ...
}

1.10.2 Пример функции с условным оператором

Допустим, нам жизненно неободима функция, которая будет определять, является число четным или нечетным, потому что сами мы постоянно путаемся…

Вот она:

odd_even <- function(x) { # функция принимает на вход число
  
  if (x %% 2 == 0) { # проверяет, равняется ли нулю остаток от деления числа на два
    
    return("even") # возвращает "even", если равняется
    
  } else {
    
    return("odd") # возвращает "odd", если нет
    
  }
  
}

odd_even(2)

[1] "even"

odd_even(34)

[1] "even"

odd_even(11)

[1] "odd"

odd_even(135)

[1] "odd"

Работает!

1.11 Пример функции из реального проекта с условным оператором

Важно!

Вам не нужно сейчас подробно понимать, что написано ниже — мы все разберем по ходу курса и научимся писать такое же! Сейчас главное ухватить структуру условного оператора — где условие, что выполняется, если условие верно, что выполняется, если условие ложно. Всё! Остальное освоим по ходу дела.

ms_preproc <- function(d) {
  
  require(tidyverse)
  
  # Since we our participants could fill the fields in any order, 
  # here is a function which allows us to count correct inputs 
  # our subjects made.
  
  if ("mouse_MSe.time" %in% colnames(d)) { 
    ### здесь начинается условный оператор, который проверяет, есть ли такая колонка
    ### если колонка есть, то запускается код ниже
    
    d |> select(
      "Индивидуальный_код",
      matches("^noun"),
      matches("resp\\d\\.text$"),
      "mouse_MSe.time"
    ) |>
      filter_at(vars(paste0("noun", 1:3)), all_vars(!is.na(.))) |>
      filter_at(vars(paste0("noun", 4:7)), all_vars(is.na(.))) |>
      mutate(task = "MS",
             level = "easy") |>
      rename(
        "resp1" = resp1.text,
        "resp2" = resp2.text,
        "resp3" = resp3.text,
        "id" = "Индивидуальный_код",
        "rt" = "mouse_MSe.time"
      ) |>
      select(-c(paste0("noun", 4:7))) -> MS
    
  } else {
    ### а если колонки нет, то запускается этот код
    
    d |> select("Индивидуальный_код",
                matches("^noun"),
                matches("resp\\d\\.text$")) |>
      filter_at(vars(paste0("noun", 1:3)), all_vars(!is.na(.))) |>
      filter_at(vars(paste0("noun", 4:7)), all_vars(is.na(.))) |>
      mutate(task = "MS",
             level = "easy",
             rt = NA) |>
      rename(
        "resp1" = resp1.text,
        "resp2" = resp2.text,
        "resp3" = resp3.text,
        "id" = "Индивидуальный_код"
      ) |>
      select(-c(paste0("noun", 4:7))) -> MS

  }
  
  return(MS)
  
}

1.12 Вне функций

Вне функций условный оператор практически не используется, потому что для предобработки данных есть удобная функция ifelse().

1.13 Циклы

То, что мы написали функция, чтобы не дублировать код — это хорошо, однако эту функцию нам все равно придется запускать много раз, если нам надо этот кусок кода повторить.

Поэтому используем цикл:

for (i in a:b) {
  ...
  body
  ...
}

1.14 Пример простеньких циклов

Просто печатаем числа от 1 до 10:

for (i in 1:10) {
  print(i)
}

[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10

Ну, или более сложные выражения:

for (j in 1:10) {
  print(sqrt(j) + j^2)
}

[1] 2
[1] 5.414214
[1] 10.73205
[1] 18
[1] 27.23607
[1] 38.44949
[1] 51.64575
[1] 66.82843
[1] 84
[1] 103.1623

1.15 Пример цикла для чтения и предоработки данных

Важно!

Вам не нужно сейчас подробно понимать, что написано ниже — мы все разберем по ходу курса и научимся писать такое же! Сейчас главное ухватить структуру цикла — где итератор и где тело, которое будет выполняться несколько раз. Всё! Остальное освоим по ходу дела.

for (i in 1:length(files)) { ## будем двигаться от 1 до количества файлов в папке с данными
  
  print(files[i]) ## печатает имя файла, чтобы видеть на каком файле сломалось, если сломается
  
  d <- read_csv(files[i], show_col_types = FALSE) ## считывает один файл из папки
  
  ## запускаем функции предобработки
  MR_data |> bind_rows(mr_preproc(d) |> mutate(file = files[i])) -> MR_data
  ST_data |> bind_rows(st_preproc(d) |> mutate(file = files[i])) -> ST_data
  MS_data |> bind_rows(ms_preproc(d) |> mutate(file = files[i])) -> MS_data
  NASATLX_data |> bind_rows(nasatlx_preproc(d) |> mutate(file = files[i])) -> NASATLX_data
  SEQUENCE_data |> bind_rows(sequence_preproc(d) |> mutate(file = files[i])) -> SEQUENCE_data
  
  ## завершили цикл, идем на следующую итерацию

}

1.16 Циклы в R — это зло! Они долго работают!

Да, циклы работают не быстро — это правда. Но, с другой стороны, мы и не терабайты данных анализируем.

Допустим, у нас 50 респондентов. Цикл, подобный тому, что на предыдущем слайде, отбработает секунды за 3. Даже чай не успеете заварить.

Безусловно, есть более изящные и быстрые инструменты, и с ними мы познакомимся на предобработке данных. Но в целом, можно и циклом обойтись.

Конечно, если у вас огромные датасеты и вы работаете с Big Data, то прогон цикла может значительно затянуться — в этом случае разумно сразу использовать другие инструменты.

По пути надо ещё не перепутать с R-Studio, которая восстанавливает данные с диска. Критическое сходство названий двух программ обязывает к повышенной внимательности при написании работ/статей/отчётов/заявок на гранты, в которых вы ссылаетесь на RStudio — иногда рецензенты весьма недоумевают, как исследователи анализировали данные с помощью ПО для восстановления данных…↩︎

1.1 Установка R и RStudio

1.2 R как язык программирования. Команды

1.2.1 Математические операции

1.2.2 Математические функции

1.2.3 Логические операции

1.2.4 Переменные и объекты

1.3 Типы данных

1.3.1 numeric

1.3.2 integer

1.3.3 complex

1.3.4 character

1.3.5 factor

1.3.6 Специальные литералы

1.3.6.1 NA

1.3.6.2 NaN

1.3.6.3 NULL

1.4 Структуры данных

1.4.1 Датафрейм

1.4.2 Векторы

1.4.2.1 Индексация векторов

1.4.2.2 Векторизация

1.4.2.3 Recycling

1.5 Матрицы

1.5.1 Индексация матриц

1.6 Массивы

1.7 Списки

1.7.1 Индексация списков

1.8 Собираем датафрейм

1.8.1 Индексация датафрейма

1.9 Функции

1.9.1 Синтаксис функции

1.9.2 Пример функции

1.9.3 Пример более полезной функции

1.10 Условный оператор

1.10.1 Структура условного оператора

1.10.2 Пример функции с условным оператором

1.11 Пример функции из реального проекта с условным оператором

1.12 Вне функций

1.13 Циклы

1.14 Пример простеньких циклов

1.15 Пример цикла для чтения и предоработки данных

1.16 Циклы в R — это зло! Они долго работают!

1.3.1 `numeric`

1.3.2 `integer`

1.3.3 `complex`

1.3.4 `character`

1.3.5 `factor`

1.3.6.1 `NA`

1.3.6.2 `NaN`

1.3.6.3 `NULL`