14 L15 // Структурное моделирование и конфирматорный факторный анализ
14.1 Крайне краткое введение в структурное моделирование
Вспомним, кто мы… Мы же с вами исследователи из области социальных и/или гуманитарных наук. А чем мы богаты? Теоретическими моделями, на которых мы основываем наши исследования! А какая теоретическая модель хороша? Та, которая получила эмпирическое подтверждение1!
А как это?…
Мы научились искать факторы, скрытые за наблюдаемыми переменными — это уже большой шаг. Однако недостаточный. И главное ограничение PCA и EFA — это то, что мы ищем независимые факторы/главные компоненты, в то время как структура взаимосвязей между латентными переменными может быть гораздо сложнее. Кроме того, эти скрытые переменные могут предсказывать другие наблюдаемые переменные: например, уровень вовлеченности сотрудников [возможно] будет предсказывать выполнение KPI, что в свою очередь предсказывает заработную плату. То есть в данным случае мы движемся не от наблюдаемых переменных к латентным, а в обратном направлении. А ведь влияние одних латентных конструктов могут быть опосредованы другими… И в итоге получается что-то такое:
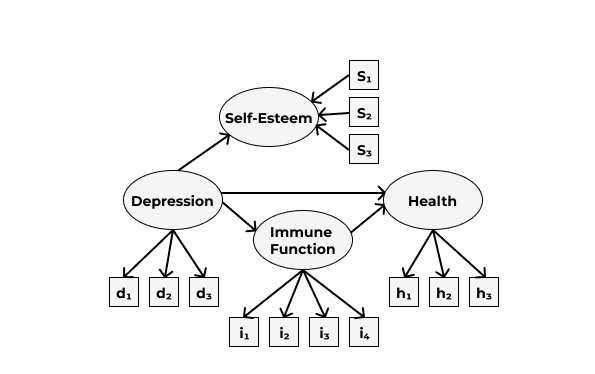
Модель может быть сколь угодно сложна — и надо её каким-то образом эмпирически проверять. Это позволяют делать структурное моделирование (structural equation modelling, SEM).
Это группа методов, которые позволяют проверять модели (гипотезы), описывающие наши данные. Проверка состоит из двух больших шагов:
- задание теоретической модели генерации данных;
- проверка того, насколько предложенная модель хорошо подходит под наши данные.
Но, если вдуматься, то так работают все статистические методы — даже в линейной регрессии мы сначала задаём линейную модель, а потом проверяем, насколько хорошо она описывает взаимосвязи, представленные в данных. В чем же особенность SEM?
Во-первых, в модель включаются латентные переменные — мы получаем возможность их моделировать и использовать для предсказаний. Этого не может делать, например, хорошо знакомая нам линейная регрессия, так как она работает только с наблюдаемыми переменными.
Во-вторых, в модель могут быть включены косвенные связи — связи между латентными переменными. То есть мы можем моделировать связи между переменными, которые мы даже не можем измерить!
Кроме того, модели удобно визуализируются с помощью диаграмм, аналогичных рисунку выше.
Возникает вопрос: сколько нужно данных для такого?
Можно ли рассчитать объем выборки, который необходим для проверки подобных гипотез? Можно, однако здесь есть некоторая проблемка.
Статистические расчеты дадут некоторый результат, но количество респондентов (наблюдений) часто оказывается далеким от необходимого —- статистика расходится с алгоритмами. Задача подбора SEM-моделей, конечно же, не имеет аналитического решения — с ним мы попрощались ещё на общих линейных моделях. Для того, чтобы параметры модели были достаточно точно подобраны, как правило, необходимо больше данных, чем говорят статистические расчеты.
Есть мнение, что «структурное моделирование требует большого количества данных». Не очень понятно, что считать большим количеством, однако эвристика следующая: на один оцениваемый параметр нужно не менее 10–15 наблюдений. Выглядит как что-то приемлемое.
14.2 Модель конфирматорного факторного анализа
Мы кратко взглянули на то, что такое структурное моделирование. Если мы возьмем от него только часть, то получим конфирматорный факторый анализ (confirmatory factor analysis). Осталось понять, какую часть надо взять.
Наша задача — проверить факторную структуру данных, которую мы взяли из теории или нашли с помощью эксплораторного факторного анализа. То есть, в общем виде что-то такое:
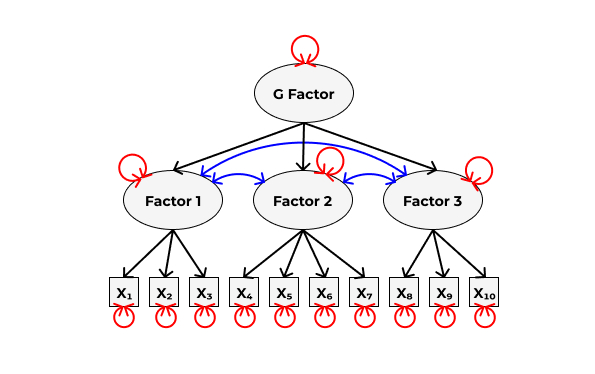
Выглядит уже не так страшно и запутанно.
В теоретической модели могут присутствовать различные типы связей:
- измерения — связи между наблюдаемыми и латентными переменными (латентные → наблюдаемые)
- и корреляции — связи между наблюдаемыми или латентными переменными (наблюдаемые → наблюдаемые, латентные → латентные)
Также, как и вообще в любой модели, сущесвуют остатки — вариантивность переменных, которую не удалось смоделировать.
В SEM также есть регрессии — связи от наблюдаемых переменных к латентным (наблюдаемые → латентные)
Как это всё работает внутри? Сложно. Но, на самом деле, за всем стоит привычная нам множественная линейная регрессия и уже знакомый нам метод максимального правдоподобия, ведь мы всё ещё в рамках линейных моделей.
Чуть выше мы обсуждали, сколько нужно данных, и сказали, что «10 наблюдений на один параметр». Однако тактично умолчали, что есть такое параметр. Так вот параметры — это, проще говоря, стрелочки на схеме выше. Это либо факторные нагрузки, так же как и в EFA, или коэффициенты косвенных связей между латентными переменными.
Конфирматорный факторный анализ в некотором смысле дополняет эксплораторный. Так, он позволяет уточнить и дополнить результаты последнего, а именно ответить на вопросы:
- пересекаются ли факторы? — действительно ли каждый переменная обусловлена влиянием одного фактора?
- достоверны ли статистически факторные нагрузки?
- как коррелируют сами факторы и как это влияет на факторные нагрузки?
- отличается ли дисперсия фактора от нуля? — ведь если нет, тогда этот фактор не информативен, то есть не дифференцирует респондентов
14.3 Оценка качества модели
Чтобы проверить, согласуются ли эмпирические данные с теоретической моделью, хочется использовать какой-то статистический тест. Однако и тут есть проблема…
Такой тест есть — это chi-squared for model fit. Его нулевая гипотеза гласит, что модель соответствует данным, а альтернативная — что модель не соответствует им. Проблема с этим тестом в том, что на больших выборках он всегда дает статистически значимые результаты, а значит мы всегда будем вынуждены отклонять нулевую гипотезу, чего делать нам крайне не хотелось бы. Поэтому на практике результаты этого статистического теста даже не приводятся, а вместо него используют метрики качества модели.
Их много, но самых популярных шесть. Для каждой из них определены пороговые значения.
| Метрика | Значение |
|---|---|
| GFI, goodnes of fit (аналог \(R^2\)) | \(>0.95\) |
| AGFI, adjusted goodnes of fit | \(>0.90\) |
| CFI, comparative fit index | \(>0.95\) |
| TLI, Tucker Lewis index | \(>0.95\) |
| RMSEA, Root Mean Square Error of Approximation | \(<0.05\) |
| SRMR, Standardized Root Mean Square Residual | \(<0.05\) |
14.4 Изучение параметров модели
КФА позволяет прямо статистически протестировать гипотезы о значимости параметров модели (факторных нагрузок, корреляций). Для этого используется следующая нехитрая таблица:
| Связь | Оценка параметра | SE | z | p | Доверительный интервал |
|---|---|---|---|---|---|
| F1 =~ q1 | 0.787 | 0.020 | 39.421 | 0.000 | [0.748, 0.827] |
| F1 ~~ F2 | 0.674 | 0.032 | 21.123 | 0.000 | [0.611, 0.736] |
Аналогично можно протестировать и значимость остатков.
Кроме статистической значимости, разумно посмотреть и на само значение оценки параметра. Так, если факторная нагрузка меньше 0.4, то можно рассмотреть вариант исключения вопроса из опросника, так как он не очень сильно связан с фактором (латентной переменной).
14.5 Модификация модели
Конфирматорный факторный анализ предполагает наличие некоторой модели, структуру которой мы проверяем на данных. Однако вполне может быть, что наша изначальная модель не учитывает что-то, что присутствует в данных.
Допустим, наша изначальная модель выглядела так:
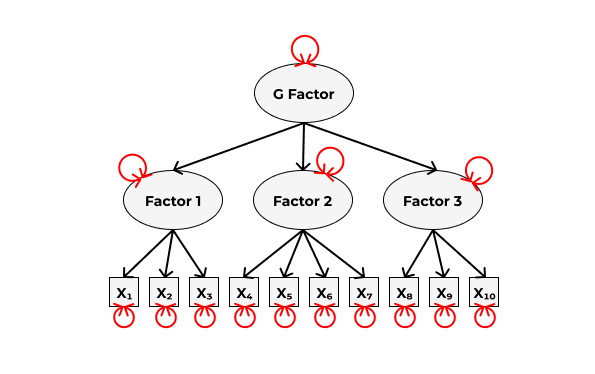
КФА позволяет проверить, насколько связи, не включенные в модель, потенциально улучшают качество модели. Для этого существуют индексы модификации (modification indices). Это относительная мера того, насколько улучшится наша модель, если мы включим в неё данную связь. Индексы модификации рассчитываются для всех связей, которые могут быть включены в модель.
Есть большой соблазн включить в изначальную модель связи с высокими индексами модификации, чтобы улучшить модель — особенно в случае, когда метрики качества модели не очень хороши. Так делать не надо. Это p-hacking.
Как же нам тогда их использовать на благо аналитики? Схема такова:
- изучить индексы модификации и выявить связи с наибольшими индексами модификации
- попробовать найти теоретическое основание таких связей
- включить их в теоретическую модель
- собрать новые данные
- проверить обновленную модель на новых данных
И по результатам анализа сделать вывод о новой модели.
В частности, у нас может получиться такая модель, если мы включим корреляции с высокими индексами модификации между факторами и пунктами опросника:
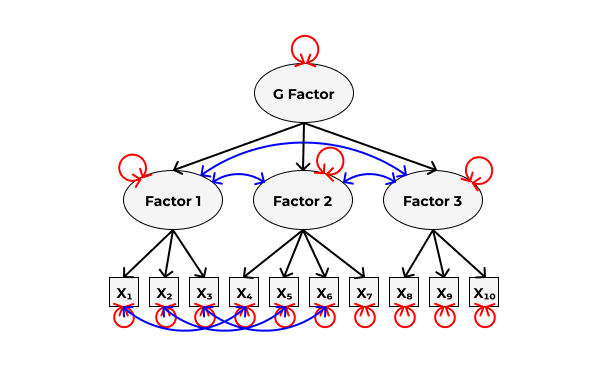
14.6 Сравнение моделей
Для сравнения моделей, во-первых, подойдут метрики качества моделей, а во-вторых, можно использоваться хи-квадрат тест, аналогично тому, как мы делали в обобщенных и смешанных линейных моделях. Также рассчитываются и информационные критерии, которые также позволяют сравнивать модели друг с другом.
Это, конечно, не единственный критерий, но, пожалуй, один из самых важных.↩︎