P7 // Случайный эксперимент. Случайные величины

Основные задания

#1

Какова вероятность, что при броске трехгранного игрального кубика:

1. выпадет число от 1 до 3?
2. выпадет 1?
3. выпадет 3?
4. выпадет 4?

Описание формата инпута.

#2

Какова вероятность, что при броске четырехгранного игрального кубика выпадет:

1. выпадет 1?
2. выпадет 1 или 2?
3. выпадет 1, 2 или 3?
4. выпадет 2 или 4?

Описание формата инпута.

#3

По ссылке расположен файл .RData с симуляцией двух четырехгранных игральных кубиков dice1 и dice2. Один из них является честным, другой — нечестным.

Выясните, каким именно является каким.

Описание формата инпута.

#4

Если дискретная случайная величина определена на конечном множестве элементрных исходов, то её функцию вероятности можно задать с помощью таблицы:

$X$	$x_1$	$x_2$	$x_3$	$...$	$x_n$
$\mathbb{P}(X=x)$	$p_1$	$p_2$	$p_3$	$...$	$p_n$

Тогда математическое ожидание такой случайной величины будет определяться следующим образом:

$$\mathbb{E}(X)=\sum _{i=1}^n{x}_i{p}_i$$

Дана случайная величина $X$ со следующей функцией вероятности:

$x$	$0$	$2$	$4$	$8$	$9$
$\mathbb{P}(X=x)$	$0.2$	$0.3$	$0.1$	$0.15$	$0.25$

Найдите математическое ожидание данной случайное величины.

Отсюда можно скачать таблицу, задающую функцию вероятности этой случайной величины.

Описание формата инпута.

#5

По таблице функции вероятности дискретной случайной величины можно найти и её дисперсию. Она определяется по формуле:

$$\text{var}(X)=\mathbb{E}(X^2)-(\mathbb{E}(X){)}^2$$

Для случайной величины из предыдущего задания найдите её дисперсию.

Описание формата инпута.

#6

Рассчитайте дисперсию следующей случайной величины:

$x$	$-2$	$-1$	$1$	$3$	$4$
$\mathbb{P}(X=x)$	$0.35$	$0.28$	$0.16$	$0.05$	$0.16$

Тут можно скачать таблицу.

Описание формата инпута.

#7

Визуализируйте функцию вероятности случайной величины из предыдущего задания.

Описание формата инпута.

#8

Некоторая случайная величина подчиняется нормальному распределению с параметрами $\mu =1.5$ и ${\sigma }^2=2.1$. Визуализируйте график функции плотности распределения этой случайной величины.

Описание формата инпута.

#9

Рассчитайте вероятность того, что случайная величина $X\sim \mathcal{N}(1.5,2.1)$ из предыдущего задания принимает значения:

1. меньшие 5
2. большие 4
3. от -1 до 1

Описание формата инпута.

#10

Вы генерируете ID для ваших респондентов как случайную последовательность пяти буквенных символов. Используются только латинские буквы нижнего регистра. В каждом случае символ выбирается случайно. Какова вероятность, что вы сгенерируете ID из пяти одинаковых символов?

Описание формата инпута.

#11

Чтобы набрать выборку для качественное апробации новой психометрической методики вы обратились в три рекрутинговых агенства. Первое агенство нашло для вас 130 потенциальных респондентов, второе — 201, третье — 94. Из интернет отзывов известно, что среди респондентов первого агенства в среднем попадается 5% профессиональных респондетов, второго — 7%, а третьего — 2.5%.

Из всех потенциальных респондентов вы выбираете рандомизатором случайного. Какова вероятность, что это профессиональный респондент?

Описание формата инпута.

#12

Выбранный вами в предыдущем задании респондент действительно оказался профессиональным. Какова вероятность, что он был рекрутирован

• первым агенством?
• вторым агенством?

Описание формата инпута.

#13

Студент решает тест из 10 вопросов. Он вообще не в курсе по какому предмету этот тест, поэтому отвечает наугад. В каждом вопросе теста четыре варианта ответа, только один из которых правильный. Тест хорошо сконструирован, поэтому все альтернативы в каждом вопросе равнозначны, а вопросы не связаны друг с другом.

Какова вероятность, что бедолага-студент:

1. ответит на все вопросы верно?
2. ответит на все вопросы неверно?

Описание формата инпута.

#14

Чтобы сдать тест, бедному студенту из предыдущео задания необходимо ответить правильно хотя бы на 6 любых вопросов. Какова вероятность, что наш студент сдаст тест?

Описание формата инпута.

#15

Известно, что распределения — даже нормальное — могут быть разными. Достаточно часто — примерное всегда — нам придется сравнивать случайные величины друг с другом на основе их распределений. Однако распределения с разными параметрами сравнивать достаточно трудно — нам надо научиться приводить разные распределения к одним и тем же параметрам.

У нас есть два распределения — $\mathcal{N}(0,5)$ и $\mathcal{N}(3,5)$. Обоснуйте, что из всех значений второго распределения можно вычесть $3$ и превратить его в первое распределение.

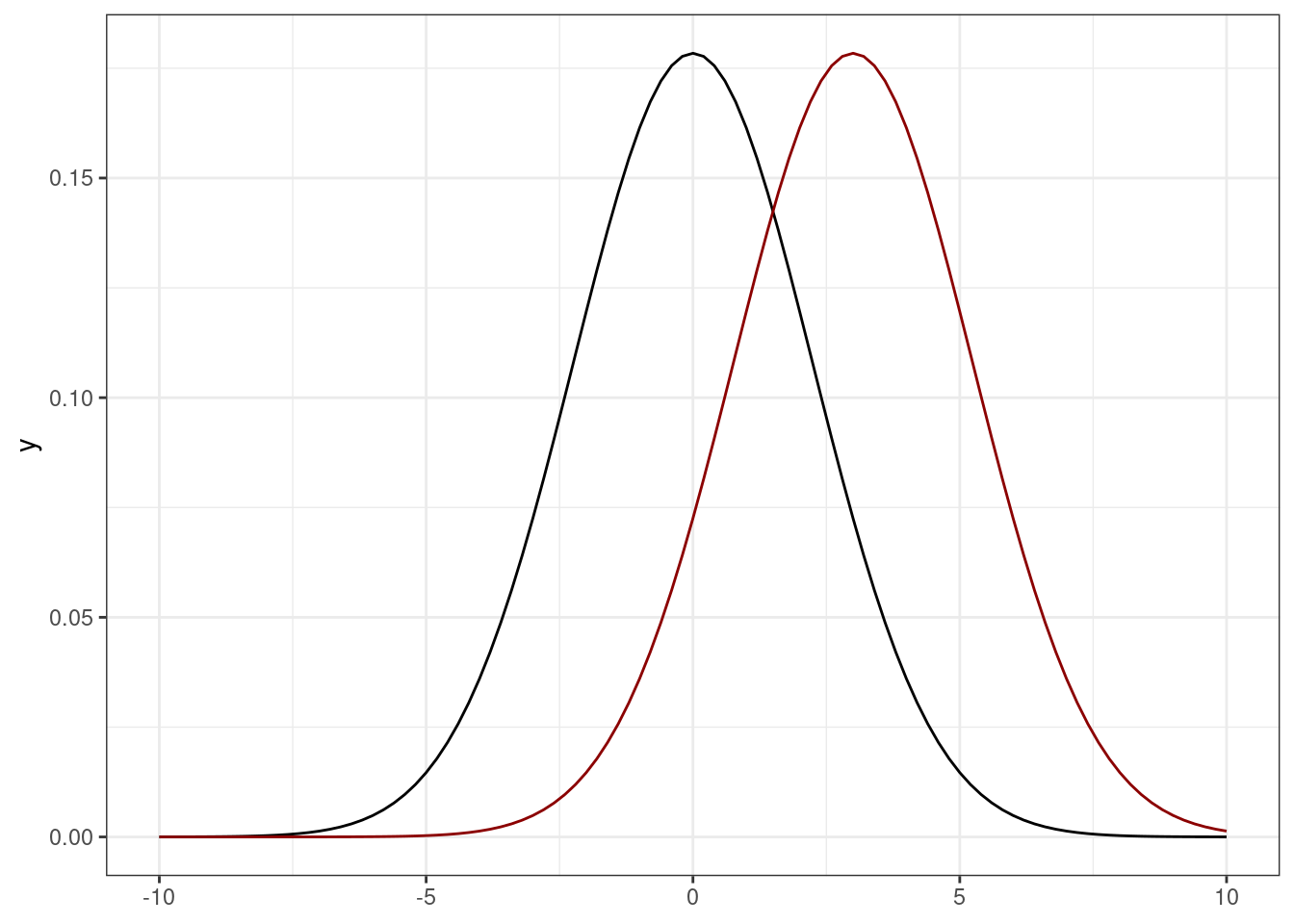
Описание формата инпута.

#16

Подолжает делать возможным сравнение разных распределений.

У нас есть два распределения — $\mathcal{N}(0,1)$ и $\mathcal{N}(0,10)$. Обоснуйте, что можно все значения второго распределения поделить на $\sigma =\sqrt{10}$ и превратить его в первое распределение.

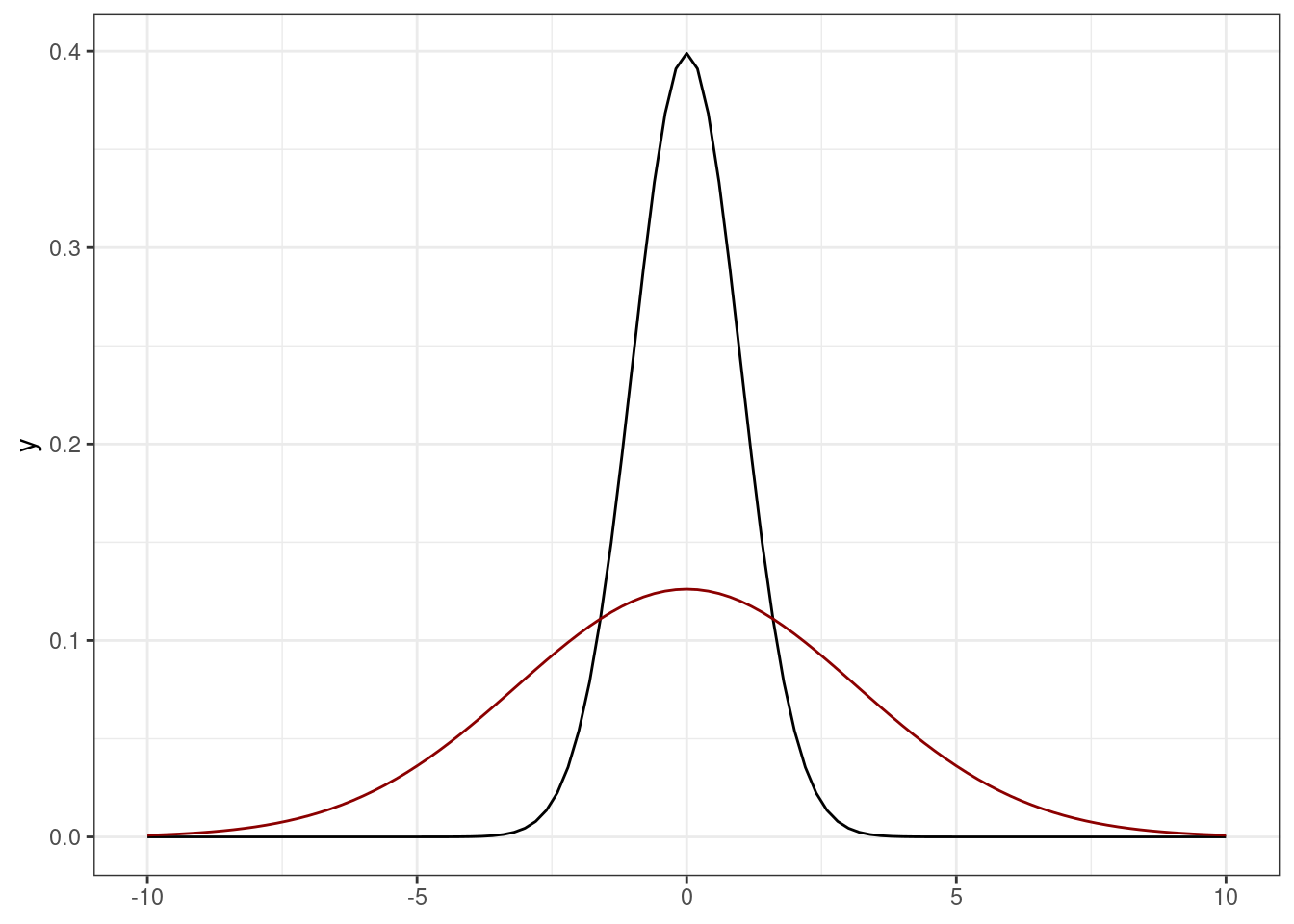
Описание формата инпута.

#17

Если мы соединим две операции из предыдущих заданий, мы получим стандартизацию. Эта операция приводит любое нормальное распределение к стандартному нормальному распределению $\mathcal{N}(0,1)$.

$$z_i=\frac{x_i-\overline{x}}{{\sigma }_x}$$

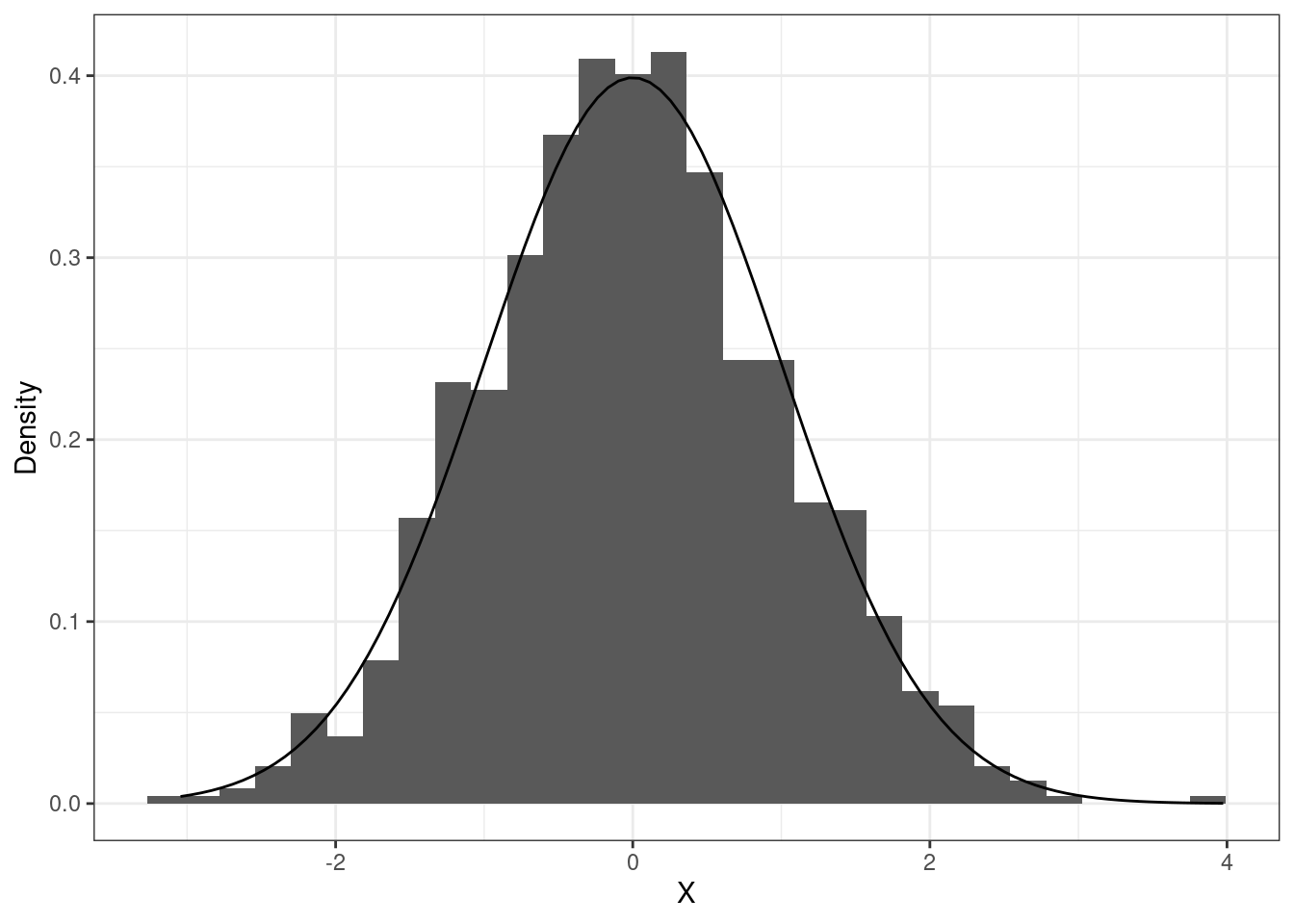
1. Сгенерируйте нормально распределенную случайную величину (1000 значений) с параметрами $\mu =10$, ${\sigma }^2=25$ (set.seed(120)).
2. Визуализируйте распределение получившейся величины.
3. Выполните стандартизацию сгенерированной случайной величины.
4. Визуализируйте распределение стандартизированной случайной величины.

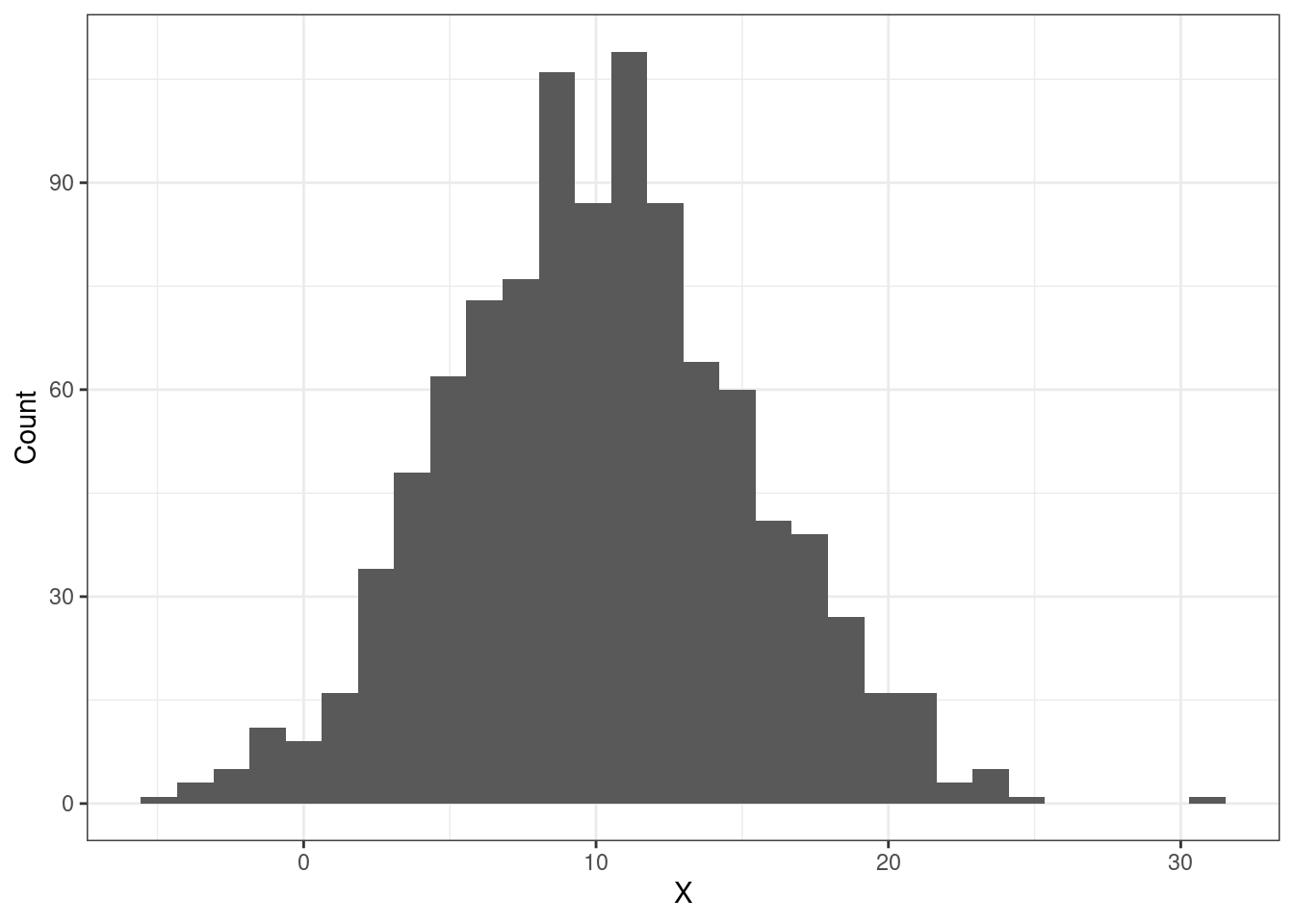
Описание формата инпута.

#18

Если можно выполнить стандартизацию, то можно выполнить и обратное преобразование — привести стандартное нормальное распределение к распределению с некоторыми параметрами $\mathcal{N}(\mu ,{\sigma }^2)$.

$$x_i=z_i\times {\sigma }_x+\overline{x}$$

Описание формата инпута.

#19

Однако стандартизировать можно в общем случае не только нормально распределенные величины, так как для любой случайной величины мы можем рассчитать среднее и стандартное отклонение. Однако здесь возникает вопрос: а не изменится ли форма распределения при выполнении стандартизации? Не потеряем ли мы какой-то важной информации?

Утверждение: стандартизация не меняет форму распределения.

Проверьте, справедливо ли это утверждение с помощью симуляции.

Описание формата инпута.

#20

Мы говорили на лекции о том, что главными характеристиками статистических данных являются неопределенность и вариативность. Давайте посмотрим, как это проявляется на распределениях.

Сгенерируйте 12 выборок по 60 наблюдений из нормального распределения $\mathcal{N}(3,4)$. Вызуализируйте распределение переменной в каждой из выборок и сравните их друг с другом.

Описание формата инпута.