14 Тестирование статистических гипотез
В ходе статистического анализа мы, главным образом, заняты тем, что тестируем статистические гипотезы. Ведь на какого рода вопросы мы отвечаем с помощью анализа?
- Различаются ли группы между собой?
- Значимо ли влияние какого-либо фактора? → Различаются ли группы между собой?
- Хороша ли та модель, которую мы построили? → Отличается ли она от нулевой модели?
И так далее. Так или иначе, всё сводится в тому, что мы ищем какие-то различия. Но силу того, что у нас неопределённость и вариация в данных, мы просто так «в лоб» сказать о различиях по оценкам параметров не можем. Приходится тестировать статистические гипотезы.
14.1 Базовые понятия
Гипотеза (\(H\)) — это предположение, которое подлежит проверке на основе результатов наблюдений.
Простая гипотеза — это такое предположение, которое включает в себя какое-либо однозначно определеяемое утверждение. Например, истинная величина параметра соответствует некоторому строго заданному значению: \(H: \theta = \theta_0\). Другой вариант — две генеральные совокупности имеют одно и то же значение одной и той же характеристики: \(H: \theta_1 = \theta_2\).
Сложная гипотеза предполагает множественность вариантов для параметра, которые укладываются в рамки проверяемого предположения. Например, \(H: \theta > \theta_0\) или \(H: \theta_1 \neq \theta_2\).
В рамках самого хода тестирования гипотез существует проверяемая (неулевая) гипотеза (\(H_0\)). Её обычно стараются предельно упростить, поэтому она формулируется как простая гипотеза. В противовес ей выдвигается альтернативная гипотеза (\(H_1\)), которая будет иметь вид сложной гипотезы.
Для проверки гипотезы нужны две вещи:
- результаты наблюдений
- критерий
Результаты наблюдений, полученные на выборке, сами по себе, как правило, не используются. Однако на их основе рассчитываются выборочные статистики, которые непосредственно участвуют в проверке гипотезы.
Критерий — это правило, согласно которому гипотезу либо принимают, либо отклоняют. Однако перед тем как проверять гипотезу, её так-то нужно сформулировать, и сделать это правильно, поскольку от формулировки гипотезы зависит интерпретация результатов проверки и дальнейшее использование полученной информации.
Используемая статистика сама по себе является [непрерывной] случайной величиной, а значит может быть построено её распределение. Критерий будет разделять это распределение на непересекающиеся области. В результате чего возникает критическая область — область отклонения гипотезы. Дополнением к ней является область неотклонения гипотезы.
Критическая область может быть односторонней (при \(H_1: \theta > \theta_0\) или \(H_1: \theta < \theta_0\)) и двусторонней (при \(H_1: \theta \neq \theta_0\)).
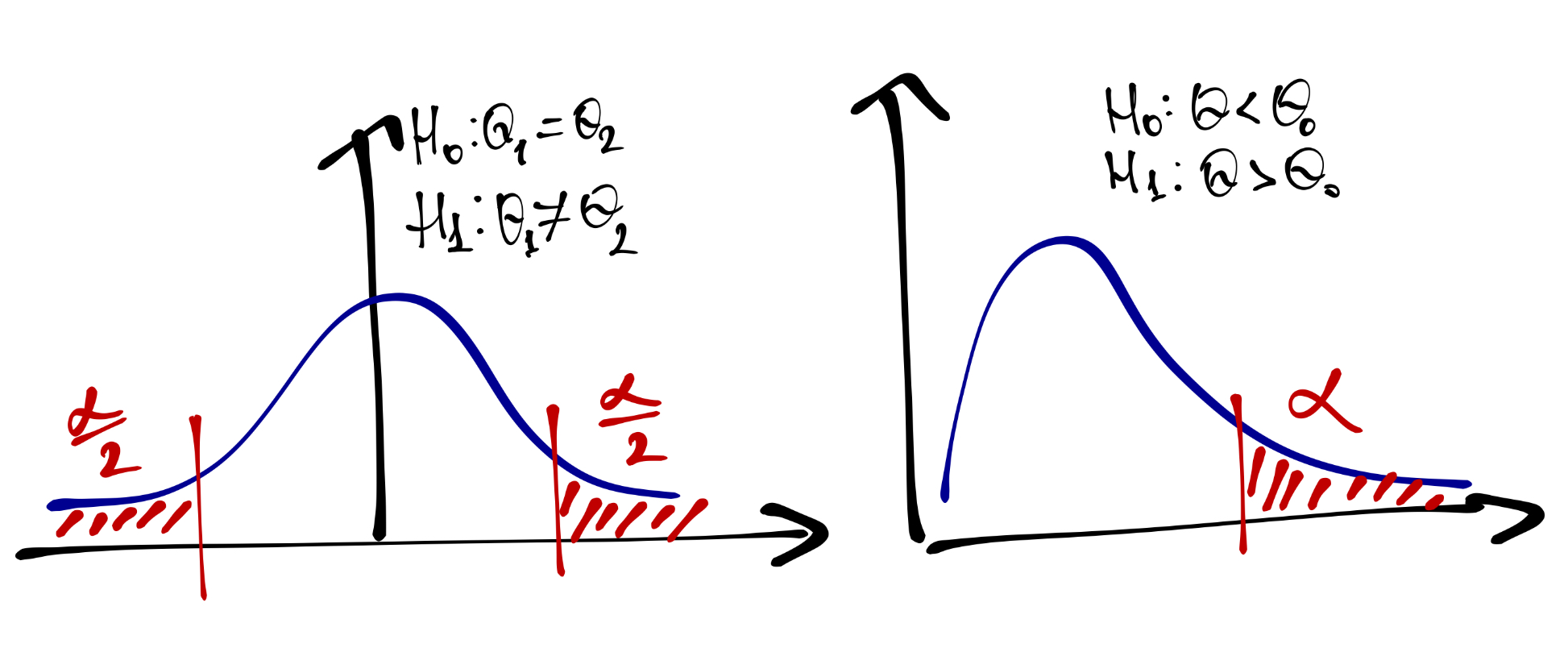
14.2 Асимметрия статистического вывода
Статистический вывод — заключение о том, получили ли мы подтверждение альтернативной гипотезы — по структур представляет собой импликацию.
Если значение нашей статистики, которое мы рассчитали на выборке, попало в критическую область, то мы говорим о том, что нулевая гипотеза отклоняется.
А если не попало? Тогда мы не можем сделать никакого вывода. Мы не получаем оснований для того, чтобы отклонить нулевую гипотезу, но и не получаем оснований, чтобы её «принять». Мы остаёмся в некотором неведении: мы не нашли различий, а есть они там или нет — хто ж их знает…
14.3 Возможные результаты проверки гипотез
На самом деле, всё чуть сложнее. Мы изучаем в исследовании какую-то закономерность, которая в реальном мире может быть, а может не быть. В силу неопределённости и вариативности наших данных мы может либо обнаружить интересующую нас закономерность, либо не обнаружить.
В качестве нулевой гипотезы мы выдвигаем предположение о том, что закономерность отсутствует — так мы упрощаем нашу нулевую гипотезу. Пусть \(H_0\) обозначает, что предположение, которое мы проверяем справедливо, а \(H_1\) — не справедливо. На основании данных мы можем либо не отклонить наше предположение (\(\hat H_0\)), либо отклонить (\(\hat H_1\)).
Тогда имеем следующую ситуацию:
| \(\hat H_0\) | \(\hat H_1\) | |
|---|---|---|
| \(H_0\) | Верное решение | Ошибка I рода |
| \(H_1\) | Ошибка II рода | Верное решение |
В терминах вероятности это выглядит так:
| \(H_0\) | \(H_1\) | |
|---|---|---|
| \(\hat H_0\) | \(\mathrm{P}(\hat H_0|H_0)\) | \(\mathrm{P}(\hat H_1|H_0) = \alpha\) |
| \(\hat H_1\) | \(\mathrm{P}(\hat H_0|H_1) = \beta\) | \(\mathrm{P}(\hat H_1|H_1) = 1 - \beta\) |
Вероятность \(\alpha\) называется уровнем значимости, вероятность \(1 - \beta\) — статистической мощностью.
При тестировании гипотез \(\alpha\) выбирается до процедуры самого тестирования и задаёт вероятность, с которой мы позволяем себе ошибиться — отклонить нулевую гипотезу, при условии, что она верна. Вероятность \(\beta\) контролировать сложнее из-за ассиметрии статистического вывода. Поэтому вводится понятие статистической мощности, которое связано с объемом выборки и размером эффекта и показывает, насколько мы можем быть уверены в том, что мы сделали всё, чтобы обнаружить закономерность. Это нам позволяет сделать вывод, что если мы не нашли интересующую нас закономерность, то он отутствует в генеральной совокупности. Статистическая мощность рассчитывается после тестирования гипотезы.
Уровень значимости \(\alpha\) выбирается близким к нулю — всем знакомо конценциональное значение \(0.05\). При выборе уровня значимости руководствуются принципом разумной достаточности, так как если устремить \(\alpha\) к нулю, что устремиться к нулю и вероятность отклонения нулевой гипотезы:
\[ \mathrm{P}(\hat H_1) = \mathrm{P}(\hat H_1 | H_0) \cdot \mathrm{P} (H_0) = \alpha \cdot \mathrm P (H_0) \]
Достаточной статистической мощностью считается \(0.8\). Аналогично, устремляя мощность к единице (\((1 - \beta) \rightarrow 1 \Rightarrow \beta \rightarrow 0\)), мы устремляем вероятность не отклонения нулевой гипотезы к нулю:
\[ \mathrm P (\hat H_0) = \mathrm P (\hat H_0 | H_1) \cdot \mathrm P (H_1) = \beta \cdot \mathrm P (H_1) \]
Необходимо также помнить, что ошибки первого и второго рода связаны между собой:
\[ \beta \cdot \mathrm P (H_1) = \mathrm P (\hat H_0) = \mathrm P (\hat H_0 | H_0) \cdot \mathrm P (H_0) \Rightarrow \beta = \frac{1}{\mathrm P (H_1)} \cdot \mathrm P (H_0) \cdot \mathrm P (\hat H_0 | H_0) \] \[ \beta = \frac{1}{\mathrm P (H_1)} \cdot \mathrm P (H_0) \cdot \big(1 - \mathrm P (\hat H_1 | H_0) \big) = \frac{1}{\mathrm P (H_1)} \cdot \mathrm P (H_0) \cdot (1 - \alpha) \]
Таким образом, \(\alpha \rightarrow 0 \Rightarrow \beta \rightarrow 1\).
14.4 Алгоритм тестирования статистических гипотез
Для тестирования гипотез есть два сценарий: первый и тот, которым мы будем пользоваться. Первый вариант чуть более классический, второй — более гибкий.
Сценарий номер раз
- Формулировка гипотезы
- Выбор статистического критерия
- Выбор уровня значимости \(\alpha\)
- Построение закона распредлеения статистики критерия при условии, что нулевая гипотеза верна
- Определение границ критической области
- Расчёт выборочной статистики
- Определение, попадает ли наблюдемое значение статистики в критическую область и вынесение решения
Сценарий номер два
- Формулировка гипотезы
- Выбор статистического критерия
- Выбор уровня значимости \(\alpha\)
- Построение закона распредлеения статистики критерия при условии, что нулевая гипотеза верна
- Расчёт выборочной статистики
- Расчёт достигнутого уровня значимости \(\alpha^*\) (мы его знаем под именем p-value)
- Сопоставление \(\alpha\) и \(\alpha^*\) и вынесение решения
Почему второй вариант более гибкий? Представим, что мы захотели понизить уровень значимости с \(0.05\) до \(0.01\) — такие уровни значимости всречаются, например, в медицине. Если мы идем по первому сценарию, то нам надо заново пересчитать критические значения и вновь проанализировать, попадает ли наблюдаемое значение в критическую область. Если мы адепты второго сценария, то нам надо только выполнить одно новое сравнение нашего p-value с новым уровнем значимости.
Разберем алгоритм тестирования статистических гипотез на примере. Останемся на просторах изучения интеллекта, только данные сгенерируем:
Итого у нас есть 50 мужчин и 50 женщин, у которых измерили коэффициент интеллекта. Нас интересует вопрос: различается ли в среднем коэффициент интеллекта у мужчин и женщин? Да, вот такой вот скучный вопрос, но что поделать. Напоминаю, что нас вообще интересует генеральная совокупность, но мы работаем с выборкой. Мы можем посчитать точечные и интервальные оценки для нашей характеристики по группам:
iq %>%
pivot_longer(cols = c("male", "female")) %>%
group_by(name) %>%
summarise(mean = unlist(mean_cl_boot(value))[1],
lower = unlist(mean_cl_boot(value))[2],
upper = unlist(mean_cl_boot(value))[3])## # A tibble: 2 x 4
## name mean lower upper
## <chr> <dbl> <dbl> <dbl>
## 1 female 112. 103. 122.
## 2 male 104. 98.6 110.По сырым зачениям вроде есть разница, но так ли это на самом деле?
Сформулируем статистическую гипотезу. Нулевая гипотеза должна быть простой, то есть говорить об отсутствии различий между группами. Так как нас интересует, если ли разница между группами или её нет, то наша альтернативная гипотеза буде двусторонней.
\[ H_0: \mu_f = \mu_m \\ H_1: \mu_f \neq \mu_m \]
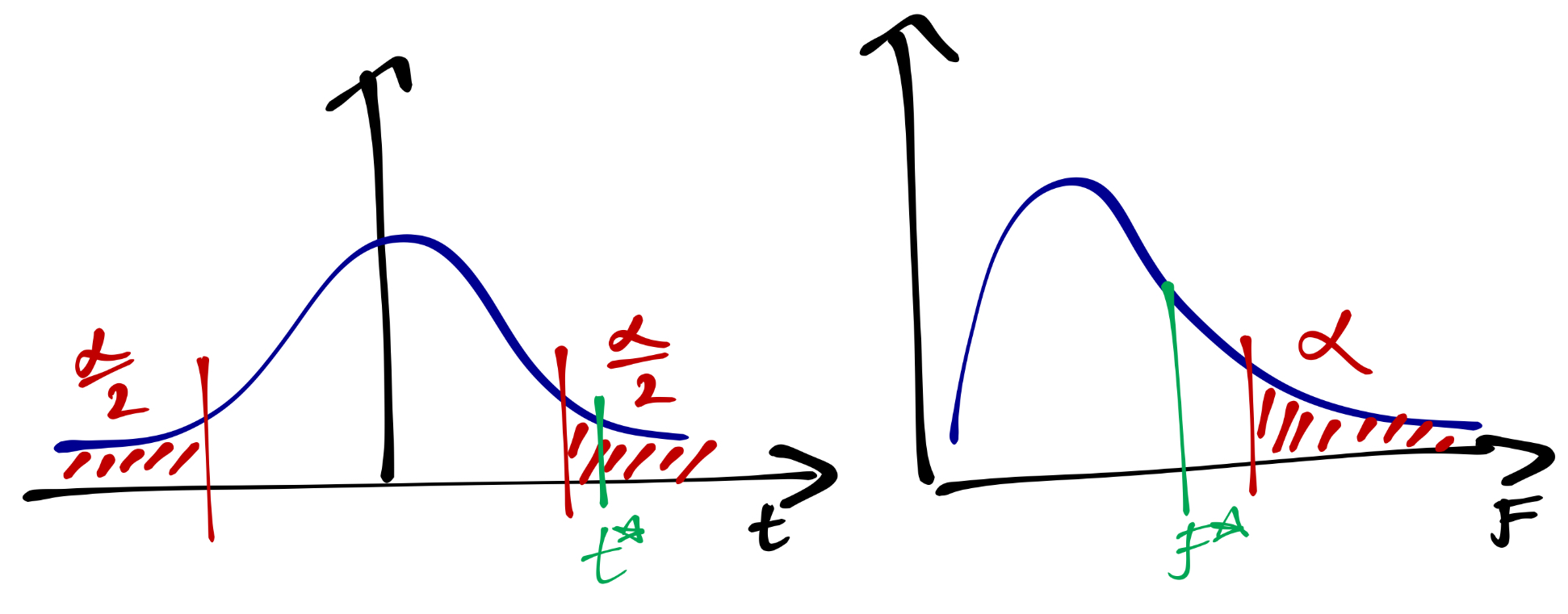
Для тестирования такой гипотезы хорошо подходит t-критерий, а именно критерий Стьюдента для двух несвязанных выборок. Его статистиска рассчитывается следующим образом:
\[ t = \frac{\bar X_1 - \bar X_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \]
Выбираем уровень значимости — останемся на конвенциональном \(0.05\).
Далее мы должны построить закон распределения статистики \(t\) при условии, что нулевая гипотеза верна, но мы воспользуемся тем, что это за нас уже сделали, и просто скажем, что закон распределения для неё известен — это \(t(\nu)\), t-распределение с параметром \(\nu\), который высчитается по этой страшной формуле:
\[ \nu = \frac{\Big(\dfrac{s_1^2}{n_1} + \dfrac{s_2^2}{n_2} \Big)^2}{\dfrac{1}{n_1-1} \Big( \dfrac{s_1^2}{n_1} \Big)^2 + \dfrac{1}{n_2-1} \Big( \dfrac{s_2^2}{n_1} \Big)^2} \]
Итого, осталось рассчитать выборочную статистику и достигнутый уровень значимости (p-value). Как радостно и приятно осознавать, что всё это в R делается ровно одной командой:
##
## Welch Two Sample t-test
##
## data: iq$male and iq$female
## t = -1.4999, df = 81.704, p-value = 0.1375
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -19.275537 2.704242
## sample estimates:
## mean of x mean of y
## 103.8269 112.1126В аутпуте мы наблюдаем значение статистики \(t\), \(\alpha^*\) для этого значения, доверительный интервал для разности средних и сами средние. Также нам представлена альтернативная гипотеза.
Что остается сделать? Сравнить \(0.1\) с \(0.05\) и заключить, что у нас нет оснований отклонить нулевую гипотезу о том, что генеральные средние равны.
14.5 Проблема множественных сравнений
Это мы сравнивали две группы между собой. Всё было хорошо. А если у нас больше двух групп? Если их пять? Десять? Или если нам нужно провести десятки тысяч сравнений1?
В одном сравнении вероятность ошибки первого рода мы задаем как \(0.05\). Когда у нас появляется много сравнений, она существенно возрастает. Почему?
Мы проводим независимые сравнения, значит вероятности ошибок будут перемножаться. Если верояность ошибиться в одном сравнении \(\alpha\), то вероятность сделать правильный вывод — \(1 - \alpha\). Тогда вероятность сделать правильный вывод в \(m\) сравнениях — \((1 - \alpha)^m\). Отсюда мы можем вывести вероятность ошибиться хотя бы в одном сравнении:
\[ \mathrm P' = 1 - (1 - \alpha)^m \]
Пусть у нас есть 3 группы, которые нам надо сравнить друг с другом — получается необходимо провести три сравнения. Итого вероятность ошибиться получается:
\[ \mathrm P' = 1 - (1 - 0.05)^3 \approx 0.143 \]
Значительно больше, чем \(0.05\). И дальше хуже. Поэтому нужно либо корректировать уровень значимости, либо использовать более мощные методы. На их изучении мы и сосредоточимся в этом курсе.
Например, в психогенетике, где мы можем сравнивать экспрессию генов.↩︎