22 Пуассоновская регрессия

В жизни и практике мы часто сталкиваемся с так называемыми счётными величинами. Например, число комнат в квартире, количество детей в семье, число книг на полке, число людей, прошедших через турникет и т.д. Глобально — любые количества. Также как счётные величины можно рассмотреть шкалу Лайкерта или оценки по десятибалльной шкале — по сути, это количество набранных баллов.

Какими свойствами обладают такие величины?

• Они могут принимать только целочисленные значения (\(x \in \mathbb Z\))
• Также возможны нулевые значения (\(0 \leq x \leq +\infty\))
• Разброс значений зависит от среднего значения (\(\mathrm{var}(X) \propto \mathbb{E}(X)\))

До сих пор мы обсуждали модели, применимые только к мерным, или непрерывным, величинам¹. Иногда свойства данных позволяют использовать такие методы для моделирования счётных величин, однако так бывает далеко не всегда.

В этой главе мы обсудим самый простой подход к моделированию счетных величин, а также одну его модификацию, которая может быть полезна.

Модели для счётных данных базируются н распределении Пуассона.

22.1 Распределение Пуассона

Распределение Пуассона опредляется следующим образом:

\[ Y \thicksim \mathrm{Poisson}(\mu) \\ f(y) = \frac{\mu^y e - \mu}{y!} \]

\(\mu\) — единственный параметр данного распределения². Он задаёт и математическое ожидание, и дисперсию, т. е.

\[ \mathbb{E}(Y) = \mu \\ \mathrm{var}(Y) = \mu \\ y \in \mathbb{N}_0 \]

Как \(\mathbb{N}_0\) здесь обозначено множество натуральных чисел с нулем.

В зависимости от того, какие значения принимает этот параметр, распределение принимает достаточно сильно различающиеся формы. При низких значения (\(\mu = 1, \mu = 2\)) в распределение присутствует сильная левосторонняя асимметрия, при высоких (\(\mu = 10\)) — распределение становится симметричным и очень похожим на нормальное распределение.

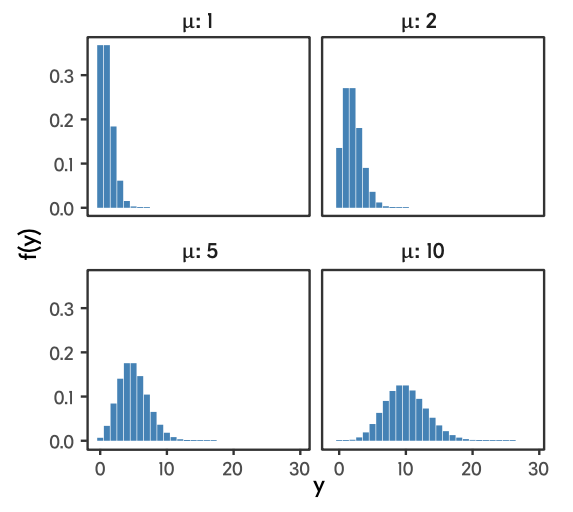
Необходимо отметить, что пуассоновское распределение предполагает, что дисперсия связана с математическим ожидание через функцию идентичности³, то есть с увеличением математического ожидания дисперсия возрастает ровно так же, как и само математичекое ожидание. Это факт нам будет важен далее.

22.2 Почему обычные регрессионные модели плохо работают на счётных данных

Ещё раз отметил два ключевых свойства пуассоновского распределения:

• множество значений целевой переменной — натуральные числа с нулём: \(y \in \mathbb{N}_0\)
• дисперсия целевой переменной зависит от матиматического ожидания: \(\mathrm{var}(Y) \propto \mathbb E(Y)\)

Первое свойство нам говорит о том, что количество не может быть отрицательным, и это логично. Обчная линейнная регрессия не имеет подобных ограничений, поэтому в предсказаниях будут появляться отрицательные значения. Что с ними делать не очень понятно.

Второе свойство говорит нам о том, что изначально не будет выполнено допущение гомоскедастичности остатков, так как чем выше математичекое ожидание, тем выше дисперсия. В итоге мы будем наблюдать воронкообразный паттер в распределении остатков:

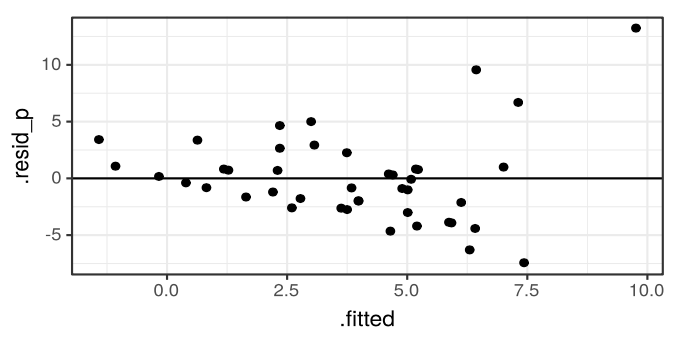
Таким образом, оценки коэффициентов модели будут неточны, ошибки завышены, а следовательно, и результатам тестирования статистической значимости параметров модели доверять нельзя.

Что делать?

Можно пойти простым путём — логарифмировать целевую переменную и построить модель для получившейся величины.

Но более корректным вариантом будет построить модель, основанную на распределении, подходящем для счётных данных. В частности, пуассоновском распределении.

22.3 Данные

Сегодня мы будем работать с данными эксперимента, в котором изучалась роль интерфейсных влияний на формирование положительного пользовательского опыта. Данные тут.

Грузим:

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.3     ✓ purrr   0.3.4
## ✓ tibble  3.1.0     ✓ dplyr   1.0.5
## ✓ tidyr   1.1.3     ✓ stringr 1.4.0
## ✓ readr   1.4.0     ✓ forcats 0.5.1

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

satis <- read_csv('https://raw.githubusercontent.com/angelgardt/hseuxlab-wlm2021/master/book/wlm2021-book/data/trust_data.csv')

## 
## ── Column specification ────────────────────────────────────────────────────────
## cols(
##   .default = col_double(),
##   id = col_character(),
##   sex = col_character(),
##   specialisation = col_character(),
##   sus_mark = col_character(),
##   explanation = col_character(),
##   feedback = col_character()
## )
## ℹ Use `spec()` for the full column specifications.

Смотрим:

str(satis)

## spec_tbl_df [120 × 31] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ id            : chr [1:120] "T1-WNBEQD" "T1-MVCbgv" "T1-zgPIDz" "T1-bQwnJq" ...
##  $ age           : num [1:120] 20 21 22 19 19 20 20 20 22 20 ...
##  $ sex           : chr [1:120] "f" "f" "m" "f" ...
##  $ specialisation: chr [1:120] "\u041f\u0441\u0438\u0445\u043e\u043b\u043e\u0433\u0438\u044f" "\u0441\u043e\u0446\u0438\u0430\u043b\u044c\u043d\u044b\u0439 \u043f\u0441\u0438\u0445\u043e\u043b\u043e\u0433" "\u044d\u043a\u043e\u043d\u043e\u043c\u0438\u043a\u0430" "\u041f\u0441\u0438\u0445\u043e\u043b\u043e\u0433\u0438\u044f" ...
##  $ freq_facebook : num [1:120] 0 1 2 0 0 1 1 0 1 0 ...
##  $ like_facebook : num [1:120] NA 1 3 NA NA 3 2 NA 2 NA ...
##  $ sort_facebook : num [1:120] NA 0 2 NA NA 2 0 NA 0 NA ...
##  $ freq_twitter  : num [1:120] 1 3 0 1 2 0 3 0 1 0 ...
##  $ like_twitter  : num [1:120] NA NA NA 4 NA 4 5 NA 4 NA ...
##  $ sort_twitter  : num [1:120] NA NA NA 1 NA 2 2 NA 1 NA ...
##  $ freq_youtube  : num [1:120] 3 1 3 0 1 3 3 3 2 3 ...
##  $ rec_youtube   : num [1:120] 1 1 1 NA 0 1 1 1 1 0 ...
##  $ why_youtube   : num [1:120] NA NA NA NA 1 NA NA NA NA 1 ...
##  $ sort_youtube  : num [1:120] 2 1 0 NA NA 1 1 2 2 NA ...
##  $ finalbtn      : num [1:120] 0 0 0 0 1 1 1 0 0 0 ...
##  $ t1            : num [1:120] 5 5 2 4 4 5 5 4 5 4 ...
##  $ t2            : num [1:120] 4 5 3 3 3 4 5 5 4 4 ...
##  $ b1            : num [1:120] 5 5 4 5 4 2 5 4 4 3 ...
##  $ sus_sum       : num [1:120] 90 77.5 87.5 82.5 75 85 90 82.5 87.5 75 ...
##  $ sus_mark      : chr [1:120] "A" "C" "B" "B" ...
##  $ time1         : num [1:120] 21245 56439 58917 58919 40417 ...
##  $ time2         : num [1:120] 83549 64750 29596 70678 84523 ...
##  $ time3         : num [1:120] 21473 3265 13161 17145 31042 ...
##  $ time4         : num [1:120] 19560 32546 28796 34088 13535 ...
##  $ errors1       : num [1:120] 1 2 1 1 0 1 1 1 0 0 ...
##  $ errors2       : num [1:120] 3 1 1 0 3 0 0 2 0 1 ...
##  $ errors_total  : num [1:120] 4 3 2 1 3 1 1 3 0 1 ...
##  $ courses       : num [1:120] 3 7 3 3 0 5 2 3 6 5 ...
##  $ group         : num [1:120] 1 1 1 1 1 1 1 1 1 1 ...
##  $ explanation   : chr [1:120] "yes" "yes" "yes" "yes" ...
##  $ feedback      : chr [1:120] "good" "good" "good" "good" ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   id = col_character(),
##   ..   age = col_double(),
##   ..   sex = col_character(),
##   ..   specialisation = col_character(),
##   ..   freq_facebook = col_double(),
##   ..   like_facebook = col_double(),
##   ..   sort_facebook = col_double(),
##   ..   freq_twitter = col_double(),
##   ..   like_twitter = col_double(),
##   ..   sort_twitter = col_double(),
##   ..   freq_youtube = col_double(),
##   ..   rec_youtube = col_double(),
##   ..   why_youtube = col_double(),
##   ..   sort_youtube = col_double(),
##   ..   finalbtn = col_double(),
##   ..   t1 = col_double(),
##   ..   t2 = col_double(),
##   ..   b1 = col_double(),
##   ..   sus_sum = col_double(),
##   ..   sus_mark = col_character(),
##   ..   time1 = col_double(),
##   ..   time2 = col_double(),
##   ..   time3 = col_double(),
##   ..   time4 = col_double(),
##   ..   errors1 = col_double(),
##   ..   errors2 = col_double(),
##   ..   errors_total = col_double(),
##   ..   courses = col_double(),
##   ..   group = col_double(),
##   ..   explanation = col_character(),
##   ..   feedback = col_character()
##   .. )

Исследовании проводилось на материале рекомендательной системы, варьировались два компонента интерфейса:

• feedback — тип фидбека:
  • good — «хороший», предъявляемый в нужном месте и нужное время
  • bad — «плохой», предъявляемый не там, где надо, и не тогда, когда надо
• explanation — объяснение работы рекомендательного алгоритма, которое могло быть представлено (yes) или скрыто от пользователя (no).

Именно эти две переменные нас будут интересовать в качестве предикторов.

В качестве зависимой переменной мы возьмем грейд по шкале SUS (System Usability Scale). Сейчас это переменная sus_mark. Однако сейчас она текстовая, нам необходимо её перекодировать в счётную числовую. Можно это сделать через ifelse(). Создадим новую переменную sus_grade:

satis$sus_grade <- recode(satis$sus_mark,
                          'A' = 5, 'B' = 4, 'C' = 3, 'D' = 2, 'E' = 1, 'F' = 0)

Вот теперь хорошо. Можно строить модель!

22.4 GLM с пуассоновским распределением целевой переменной

Мы с вами всё ещё во фреймфорке GLM, поэтому формулировка модели в общем виде будет выглядеть аналогично биномиальной регрессии:

\[ \mathrm{sus\_grade}_i \thicksim \mathrm{Poisson}(\mu_i) \\ \mathbb{E} (\mathrm{sus\_grade}_i) = \mu_i, \quad \mathrm{var}(\mathrm{sus\_grade}_i) = \mu_i \\ \ln(\mu_i) = \eta_i \]

Если в случае биномальной регрессии функция связи, использовавшаяся для линеаризации зависимости между целевой переменной и предикторами была \(\mathrm{logit}()\) и требовала много предварительных преобразований, то в данном случае всё проще: функция связи — это [натуральный] логарифм \(\ln()\). Применяя её к нашей переменной, мы получаем величину \(\eta_i\), которую можем моделировать линейной моделью.

Возьмем в качестве предикторов тип фидбека (feedback), наличие/отсутствие объяснения работы алгоритма (explanation) и их взаимодействие (feedback:explanation). Получим такую модель:

\[ \eta_i = b_0 + b_1 I_{\mathrm{feedback}_\mathrm{good}} + b_2 I_{\mathrm{explanation}_\mathrm{yes}} + b_3 I_{\mathrm{feedback}_\mathrm{good}} \cdot I_{\mathrm{explanation}_\mathrm{yes}} \]

22.4.1 Подбор модели в R

Зафитим модель в R:

model1 <- glm(sus_grade ~ feedback * explanation, data = satis,
              family = poisson)

Как видите, мы используем ту же функцию glm(), что и в случае биномиальной регрессии. Меняется только семество моделей — теперь у нас poisson.

Посмотрим summary() по модели:

summary(model1)

## 
## Call:
## glm(formula = sus_grade ~ feedback * explanation, family = poisson, 
##     data = satis)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.5820  -0.6481   0.1610   0.3539   1.7505  
## 
## Coefficients:
##                             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                   0.8893     0.1170   7.598 3.01e-14 ***
## feedbackgood                  0.3147     0.1539   2.044   0.0409 *  
## explanationyes               -0.1796     0.1735  -1.035   0.3006    
## feedbackgood:explanationyes   0.4264     0.2189   1.948   0.0514 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 183.23  on 119  degrees of freedom
## Residual deviance: 154.02  on 116  degrees of freedom
## AIC: 468.51
## 
## Number of Fisher Scoring iterations: 5

Можно заметить, что аутпут выглядит совершенно аналогично аутпуту биномиальной регрессии:

• Отсутствует \(R^2\)
• Отсутствует \(F\)-статистика, а значит и p-value для неё
• Значимость коэффициентов при предикторах тестируется при помощи z-тестов Вальда

В данному случае у нас получился один значимый предиктор — feedbackgood. Это значит, что уровень удовлетворённость пользователей, которые взаиможействовали с интерфейсом, в котором реализован хороший фидбек, отличается от уровня удовлетворенности пользователей, которые взаимодействовали с интерфейсов и плохим фидбеком. То есть данные интерфейсы формируют различный пользовательский опыт. Но насколько различный?

22.5 Интерпретация коэффициентов модели

Вспомним, что линейная модель описывает переменную \(\eta_i\), поэтому уравнение модели мы можем записать следующим образом:

\[ \eta_i = 0.89 + 0.31 I_{\mathrm{feedback}_\mathrm{good}} \]

Незначимые предикторы мы в модель включать не будем.

Так как \(\eta_i = \ln(\mu_i)\), то

• угловой коэффициент при непрерывном предикторе показывает, на сколько единиц изменится значение логарифма зависимой переменной при увеличении значения предиктора на единицу
• угловой коэффициент при категориальном предикторе показывает, на сколько единиц отличается среднее значение логарифма зависимой переменной для данной категории наблюдений по сравнению в базовым уровнем (его, как обычно, содержит intercept модели)

Само же значение зависимой переменной изменяется в \(e^{b_j}\) раз.

Таким образом, в нашем случае мы можем сказать, что sus_grade для интерфейса с хорошим фидбеков в среднем в \(e^{0.31} = 1.36\) раза выше, чем для интерфейса с плохим фидбеком. Звучит очень логично.

Однако перед интерпретацией предикторов обычно мы проверяли, значима ли модель в целом. Давайте это сделаем, а то как-то не по порядку пошли…

22.6 Анализ девиансы

В случае пуассоновской модели анализ девиансы не отличается от случая биномиальной регрессии. Нам так же нужна нулевая модель, в которой будет только интерсепт:

model_null <- glm(sus_grade ~ 1, data = satis, family = poisson)

И функция anova(), которая будет сравнивать нашу модель с нулевой. Используем test = 'Chi':

anova(model1, model_null, test = 'Chi')

## Analysis of Deviance Table
## 
## Model 1: sus_grade ~ feedback * explanation
## Model 2: sus_grade ~ 1
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1       116     154.02                          
## 2       119     183.23 -3  -29.214 2.019e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Наблюдаем, что модель статистически значима. Это очень хорошо.

22.7 Проверка на сверхдисперсию (overdispersion)

Но не совсем… Пока что мы не можем однозначно доверять данным результатам, так как не проверили одного важного прежположения, которое положили в основу пуассоновской регрессии. А именно — допущение о том, что \(\mathbb E(X) = \mathrm{var}(X)\). В общем случае ведь связь дисперсии и математического ожидания не обязательно описывается функцией идентичности.

Если дисперсия не равна среднему значению, то мы не можем доверять результатам подбора модели.

Чтобы провести проверку на сверхдисперсию, можно воспользоваться функцией, которую предложил Ben Bolker:

overdisp_fun <- function(model) {
  rdf <- df.residual(model)
  if (inherits(model, 'negbin'))
    rdf <- rdf - 1
  rp <- residuals(model, type = 'pearson')
  Pearson.chisq <- sum(rp ^ 2)
  prat <- Pearson.chisq / rdf
  pval <-
    pchisq(Pearson.chisq, df = rdf, lower.tail = FALSE)
  c(
      chisq = Pearson.chisq,
      ratio = prat,
      rdf = rdf,
      p = pval
    )
}

Проверим модель на сверхдисперсию:

overdisp_fun(model1)

##       chisq       ratio         rdf           p 
## 109.6350957   0.9451301 116.0000000   0.6486891

Данная функция рассчитывает статистику \(\chi^2\) (chisq), по которой определяет отношение дисперсии к среднему значению (ratio), и рассчитывает p-value. Так как пуассоновская модель исходит из предположения равенства дисперсии и математического ожидания, то значение ratio должно быть близко к единице. В данном случае мы это и имеем: дисперсия в 0.94 раза превышает математическое ожидание, то есть на самом деле, даже немного ниже математического ожидания. P-value говорит нам о том, что сверхдисперсии нет — мы можем доверять результатам нашей модели.

А если бы сверхдисперсия всё же была? Чем это плохо?

Для распределения Пуассона у нас есть следующие уравнения:

\[ \mathrm{var}(y_i) = \mu_i \\ \mathrm{var}(\mathbb E(y_i)) = \frac{\mu_i}{n} \\ \mathrm{SE}_{\mathbb E(y_i)} = \sqrt{\mathrm{var}(\mathbb E(y_i))} \]

Если обнаружена сверхдисперсия, то данные не подчиняются распределению Пуассона, и дисперсия в \(\varphi\) раз больше среднего (\(\varphi > 1\)). Тогда,

\[ \mathrm{var}(y_i) = \varphi \mu_i \\ \mathrm{var}(\mathbb E(y_i)) = \frac{\varphi \mu_i}{n} \\ \mathrm{SE}_{\mathbb E(y_i)} = \sqrt{\varphi \mathrm{var}(\mathbb E(y_i))} \]

А так как пуассоновская модель не знает, что там есть какое-то \(\varphi\), то:

• доверительная зона предсказаний модели будет заужена из-за того, что оценки стандартных ошибок занижены;
• тесты Вальда для коэффициентов модели дадут неправильные результаты из-за того, что оценки стандартных ошибок занижены. Уровень значимости будет занижен;
• тесты, основанные на сравнении правдоподобий, дадут смещенные результаты, т.к. соотношение девианс уже не будет подчиняться \(\chi^2\)-распределению.

Каковы могут быть причины сверхдисперсии? Перечислим основные:

• в данных есть выбросы
• в модель не включен важный предиктор или взаимодействие предикторов
• нарушена независимость выборок (есть внутригрупповые корреляции)
• выбрана неподходящая функция связи
• выбрана неподходящая функция распределения для целевой переменной

А что же делать? Пусти есть разные. Мы рассмотрим наболее простой.

22.8 Квазипуассоновские модели

Первое, что надо запомнить — «квази-пуассоновсного» распределения не бывает! Эти модели также основываются на распределении Пуассона, но учитывают тот самый коэффициент \(\varphi\), описывающий сверхдисперсию — поправка на избыточность дисперсии.

Записать квазипуассоновскую модель можно следующим образом:

\[ y_i \thicksim \mathrm{QuasiPoisson}(\mu_i) \\ \mathbb{E}(y_i) = \mu_i \\ \mathrm{var}(y_i) = \varphi \mu_i \\ \ln(\mu_i) = \eta_i \]

\(\varphi\) оценивается по имеющимся данным. Само же уравнение модели совершенно не изменится:

\[ \eta_i = b_0 + b_1 I_{\mathrm{feedback}_\mathrm{good}} + b_2 I_{\mathrm{explanation}_\mathrm{yes}} + b_3 I_{\mathrm{feedback}_\mathrm{good}} \cdot I_{\mathrm{explanation}_\mathrm{yes}} \]

22.8.1 Квазипуассоновские модели в R

Хотя мы не обнаружили избыточность дисперсии при диагностике модели, давайте построим квазипуассоновскую модель и посмотрим на её отличия от пуассоновской регрессии.

model2 <- glm(sus_grade ~ feedback * explanation, data = satis,
              family = "quasipoisson")

summary(model2)

## 
## Call:
## glm(formula = sus_grade ~ feedback * explanation, family = "quasipoisson", 
##     data = satis)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.5820  -0.6481   0.1610   0.3539   1.7505  
## 
## Coefficients:
##                             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                   0.8893     0.1138   7.815 2.74e-12 ***
## feedbackgood                  0.3147     0.1497   2.103   0.0376 *  
## explanationyes               -0.1796     0.1686  -1.065   0.2891    
## feedbackgood:explanationyes   0.4264     0.2128   2.004   0.0474 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 0.9451325)
## 
##     Null deviance: 183.23  on 119  degrees of freedom
## Residual deviance: 154.02  on 116  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 5

Взглянем на аутпут. У нас, ожидаемо, изменились результаты тестирования статистической значимости коэффициентов, хотя сами коэффициенты остались теми же самыми. Почему?

Да, оценки параметром модели в квазипуассоновских и пуассоновских моделях получаются одинаковыми, однако

• стандартные ошибки коэффициентов домножатся на \(\sqrt{\varphi}\);
• доверительные интервалы коэффициентов домножаются на \(\sqrt{\varphi}\);
• логарифмы правдоподобий, используемые для тестирования статистической значимости моделей, уменьшаются в \(\varphi\) раз.

А так как тестирование статистической значимости работает со стандартными ошибками, то и статистическая значимость также изменяется.

22.9 Особенности работы с квазипуассоновскими моделями

Кроме того, если ряд других отличий. Одно из них можно обнаружить в аутпуте функции summary(): в тестах параметров используются t-тесты и, соответственно, t-распределение в отличие от других GLM, где используются z-тесты Вальда и стандарнтное нормальное распределение.

Для анализа девиансы используются F-тесты, а не \(\chi^2\):

model_null2 <- glm(sus_grade ~ 1, data = satis, family = "quasipoisson")

anova(model2, model_null2, test = 'F')

## Analysis of Deviance Table
## 
## Model 1: sus_grade ~ feedback * explanation
## Model 2: sus_grade ~ 1
##   Resid. Df Resid. Dev Df Deviance      F    Pr(>F)    
## 1       116     154.02                                 
## 2       119     183.23 -3  -29.214 10.303 4.584e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

А также для квазипуассоновских моделей не определена функция максимального правдоподобия, поэтому нельзя вычислить AIC.

В завершении стоит отметить, что пуассоновские модели — это история, скорее, для исследователей. В индустрии даже на счетных данных чаще всего используют обычные линейные модели, хотя это и не то чтобы суперкорректно.

---

1. Не считая, конечно, биномиальную регрессию.↩

2. В отличие от нормального распределения, которое задается двумя параметрами \(X \thicksim \mathcal{N}(\mu, \sigma^2)\)↩

3. С этой функцией вы хорошо знакомы — это самая простая линейная функция вида \(y = x\).↩