21 Обобщенные линейные модели. Логистическая регрессия

21.1 Ограничения общих линейных моделей

Модели, которые мы изучали на предыдущих занятиях носят название общих линейных моделей (general linear models). Они достаточно просты и удобны в большинстве случаев, однако имеют ряд важных ограничений.

Вспомним, как выглядит уравнение такой модели: \[y = \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p + \varepsilon\]

Предикторы в такой модели могут быть как дискретными, так и непрерывными.

Важнейшим допущением / требованием этой модели является распределение ошибки: \[\varepsilon \thicksim \mathcal{N}(0, \, \sigma)\]

Поскольку ошибка модели должна быть распределена нормально, а моделируется среднее значение, то можно сформулировать более общее допущение / требование: \[y_i \thicksim \mathcal{N}(\mu_i, \, \sigma)\]

Таким образом, общие линейные модели позволяют моделировать зависимости только для нормально-распределенных величин. Если же отклик модели (он же зависимая переменная) подчиняется другому распределению, эти модели не годятся.

Однако нам на помощь приходят обобщенные линейные модели (generalized linear models), которые позволяют моделировать зависимости величин, подчиняющихся не только нормальному распределению, но и многим другим.

Мы познакомимся с общей логикой построения GLM, подробно рассмотрев один из вариантов таких моделей, а именно биномиальную регрессию.

21.2 Биномиальное распределение

Биномальное распределение описывает вероятность выпадения определенного числа «успехов» в серии испытаний Бернулли.

Здесь можно поиграться.

21.3 Бинарные переменные

Эти переменные достаточно широко распространены как повседневности, так и в науке. Блюдо вкусное или невкусное, команда выиграла или проиграла, пациент в результате медицинских манипуляций выжил или умер, в ходе эксперимента была выбрана какая-то опция или нет, сдал студент экзамен или не сдал — и т.д.

Эти события могут быть связаны с раздичными предикторами, и такую взаимосвязь можно описать с помощью регрессионных моделей.

21.4 HR-данные

Тут есть датасет про менеджеров. Это часть данных большого датасета, собранного в рамках одного из HR-исследований.

Грузим данные.

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.3     ✓ purrr   0.3.4
## ✓ tibble  3.1.0     ✓ dplyr   1.0.5
## ✓ tidyr   1.1.3     ✓ stringr 1.4.0
## ✓ readr   1.4.0     ✓ forcats 0.5.1

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

library(car)

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

theme_set(theme_bw())

managers <- read_csv('https://raw.githubusercontent.com/angelgardt/hseuxlab-wlm2021/master/book/wlm2021-book/data/managers.csv')

## Warning: Missing column names filled in: 'X1' [1]

## 
## ── Column specification ────────────────────────────────────────────────────────
## cols(
##   X1 = col_double(),
##   id = col_character(),
##   lvl = col_character(),
##   qualification = col_double(),
##   autonomy = col_double(),
##   subdiv_regulations = col_double(),
##   company_regulations = col_double(),
##   direct_juniors = col_double(),
##   func_juniors = col_double(),
##   income_influence = col_double(),
##   error_cost = col_double()
## )

Смотрим их структуру.

str(managers)

## tibble [3,210 × 11] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ X1                 : num [1:3210] 1 2 3 4 5 6 7 8 9 10 ...
##  $ id                 : chr [1:3210] "таб_1544093" "таб_1397647" "таб_4078395" "таб_4172997" ...
##  $ lvl                : chr [1:3210] "Сотрудник" "Сотрудник" "Сотрудник" "Сотрудник" ...
##  $ qualification      : num [1:3210] 5 4 2 4 5 2 5 5 2 2 ...
##  $ autonomy           : num [1:3210] 2 2 2 3 3 2 3 2 1 1 ...
##  $ subdiv_regulations : num [1:3210] 1 1 1 1 2 1 1 1 1 1 ...
##  $ company_regulations: num [1:3210] 1 1 1 1 3 1 1 1 1 1 ...
##  $ direct_juniors     : num [1:3210] 1 1 1 1 2 1 1 1 1 1 ...
##  $ func_juniors       : num [1:3210] 1 1 1 1 1 1 2 1 1 1 ...
##  $ income_influence   : num [1:3210] 1 1 1 1 3 2 1 1 1 2 ...
##  $ error_cost         : num [1:3210] 1 2 1 1 5 2 1 2 1 2 ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   X1 = col_double(),
##   ..   id = col_character(),
##   ..   lvl = col_character(),
##   ..   qualification = col_double(),
##   ..   autonomy = col_double(),
##   ..   subdiv_regulations = col_double(),
##   ..   company_regulations = col_double(),
##   ..   direct_juniors = col_double(),
##   ..   func_juniors = col_double(),
##   ..   income_influence = col_double(),
##   ..   error_cost = col_double()
##   .. )

У нас есть следуюшие переменные:

id — табельный номер сотрудника
lvl — уровень (Сотрудник или Менеджер)
qualification — профессиональная квалификация
autonomy — автономия в принятии решений
subdiv_regulations — участие в формировании регламентов подразделения
company_regulations — участие в формировании регламентов Компании
direct_juniors — количество прямых подчинённых
func_juniors — количество функциональных подчинённых
income_influence — влияние на доход Компании
error_cost — стоимость ошибки

Поизучаем данные.

colSums(is.na(managers))

##                  X1                  id                 lvl       qualification 
##                   0                   0                   0                   0 
##            autonomy  subdiv_regulations company_regulations      direct_juniors 
##                   0                   0                   0                   0 
##        func_juniors    income_influence          error_cost 
##                   0                   0                   0

table(managers$lvl)

## 
##  Менеджер Сотрудник 
##       810      2400

21.5 Задача построения линейной модели

В наших данных есть бинарная переменная lvl — она содержит две градации: Сотрудник и Менеджер. Вопрос, на который нам необходимо ответить: по каким параметрам различаются менеджеры и сотрудники?

Прежде всего надо вспомнить, что мы работаем с математической моделью, которой необходимы числа, поэтому придётся перекодировать нашу целевую переменную. Пусть 1 обозначает менеджеров, а 0 — сотрудников.

managers %>% 
  select(-X1, -id) %>% # заодно удалим лишние переменные
  mutate(lvl = ifelse(lvl == 'Менеджер', 1, 0)) -> managers

Теперь мы можем построить модель, описывающую связь lvl с имеющимися предикторами.

Попробуем обычную линейную регрессию.

model0 <- lm(lvl ~ ., managers)
summary(model0)

## 
## Call:
## lm(formula = lvl ~ ., data = managers)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.47532 -0.07671 -0.04250  0.06891  1.02042 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         -0.869056   0.015520 -55.994  < 2e-16 ***
## qualification        0.048487   0.004420  10.969  < 2e-16 ***
## autonomy             0.016780   0.008309   2.019 0.043527 *  
## subdiv_regulations   0.281009   0.014017  20.048  < 2e-16 ***
## company_regulations -0.068712   0.011403  -6.026 1.88e-09 ***
## direct_juniors       0.369140   0.012549  29.416  < 2e-16 ***
## func_juniors         0.107304   0.008069  13.298  < 2e-16 ***
## income_influence     0.072478   0.007434   9.749  < 2e-16 ***
## error_cost          -0.026336   0.007985  -3.298 0.000984 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2235 on 3201 degrees of freedom
## Multiple R-squared:  0.7361, Adjusted R-squared:  0.7354 
## F-statistic:  1116 on 8 and 3201 DF,  p-value: < 2.2e-16

Модель сошлась, всё суперклассно.

managers %>%
  mutate(
    L = qualification +
        autonomy +
        subdiv_regulations +
        company_regulations +
        direct_juniors +
        func_juniors +
        income_influence +
        error_cost
  ) %>%
  ggplot(aes(L, lvl)) +
  geom_point(size = 2, alpha = .3) +
  geom_point(aes(y = model0$fitted.values),
             color = 'darkred', alpha = 0.5)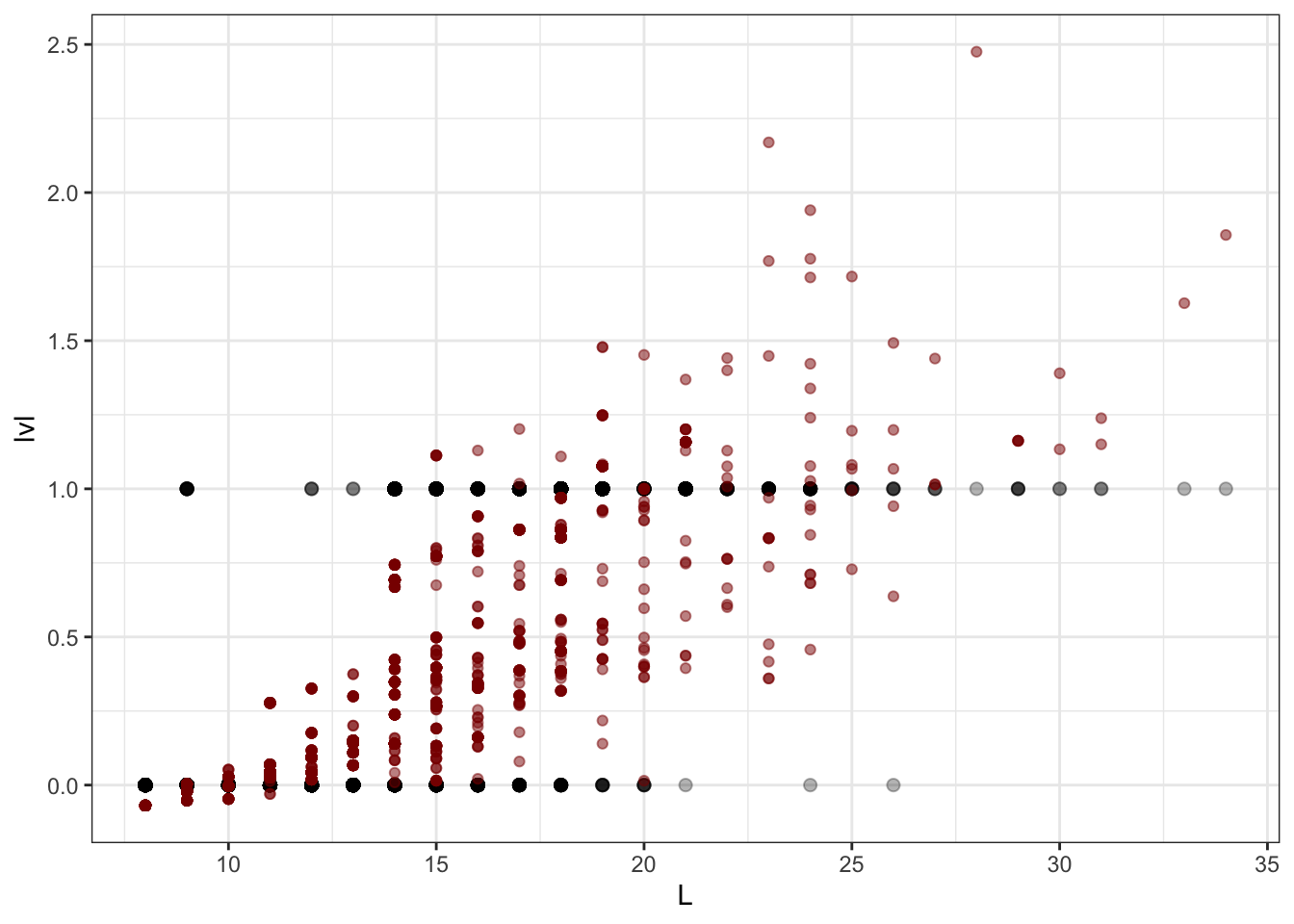

Но получается что-то странное…

Во-первых, непонятно, какая величина отложена на оси \(y\). Во-вторых, предсказания модели выходят за границы допустимых значений (модель предсказывает отрицательные и большие единицы значения). Поэтому простая линейная модель нам не подходит. Надо искать что-то еще.

21.6 Переход от дискретной величины к непрерывной

21.6.1 Логистическая кривая

Собственно бинарные переменные неудобны для работы, поэтому надо найти способ превратить такую дискретную бинарную шкалу в «безграничную» и непрерывную. При моделировании нулей и единиц переходят к моделированию вероятности получения единиц.

Сама зависимая переменная в зависимости от предиктора распределена примерно так:

Введем новые обозначения:

\(p_i\) — вероятность события \(y_i = 1\) при данных значениях предиктора,
\(1 - p_i\) — вероятность альтернативного события \(y_i = 0\).

Получается непрерывная величина \(0 \leq p_i \leq 1\).

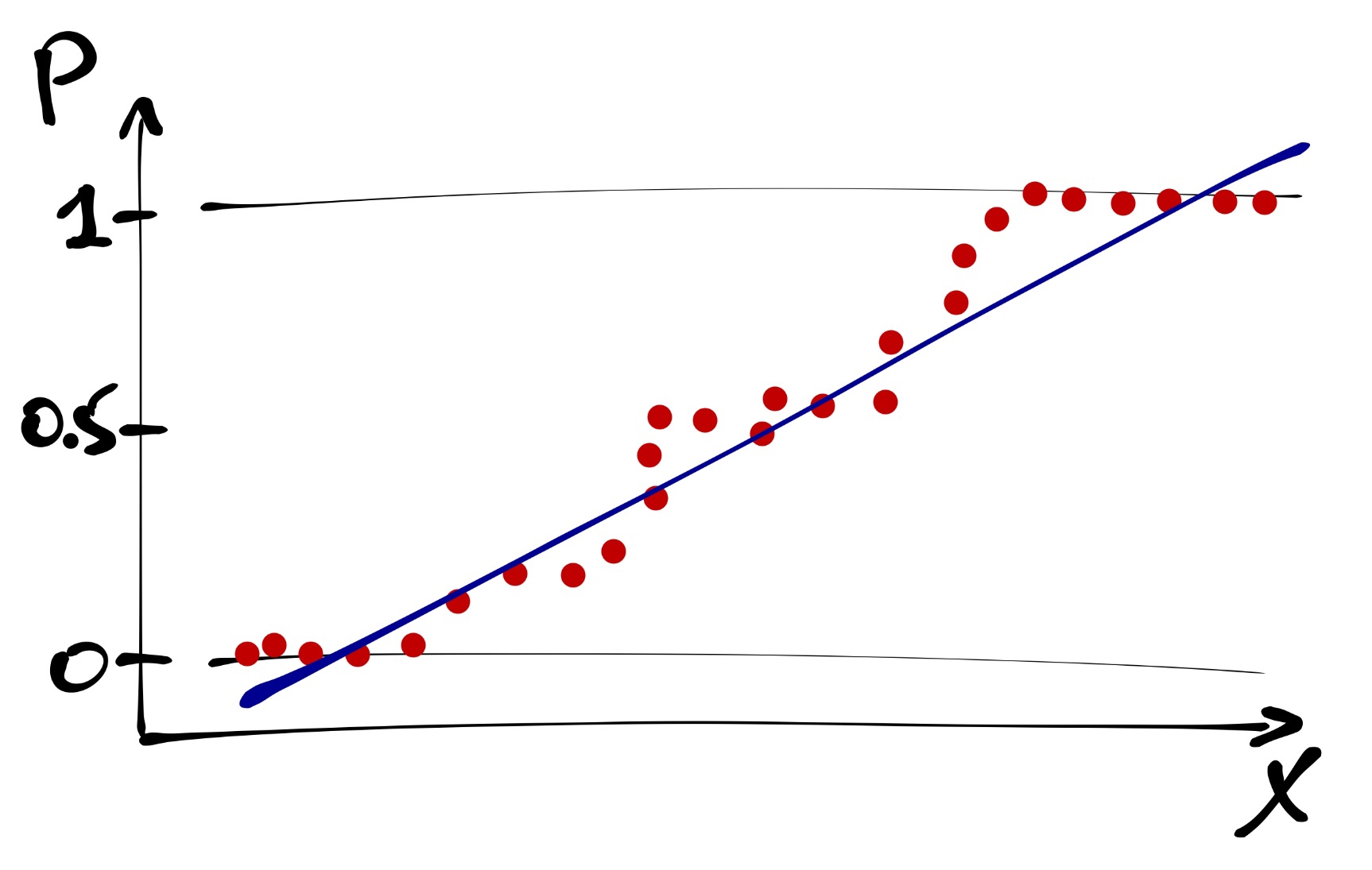
И вроде бы как ее можно уже моделировать. Но нужно помнить, что вероятность изменяется в пределах от нуля до единицы, а прямая ничем не ограничена. Поэтому прямая — не лучший вариант.

Такая закономерность моделируется логистической кривой.

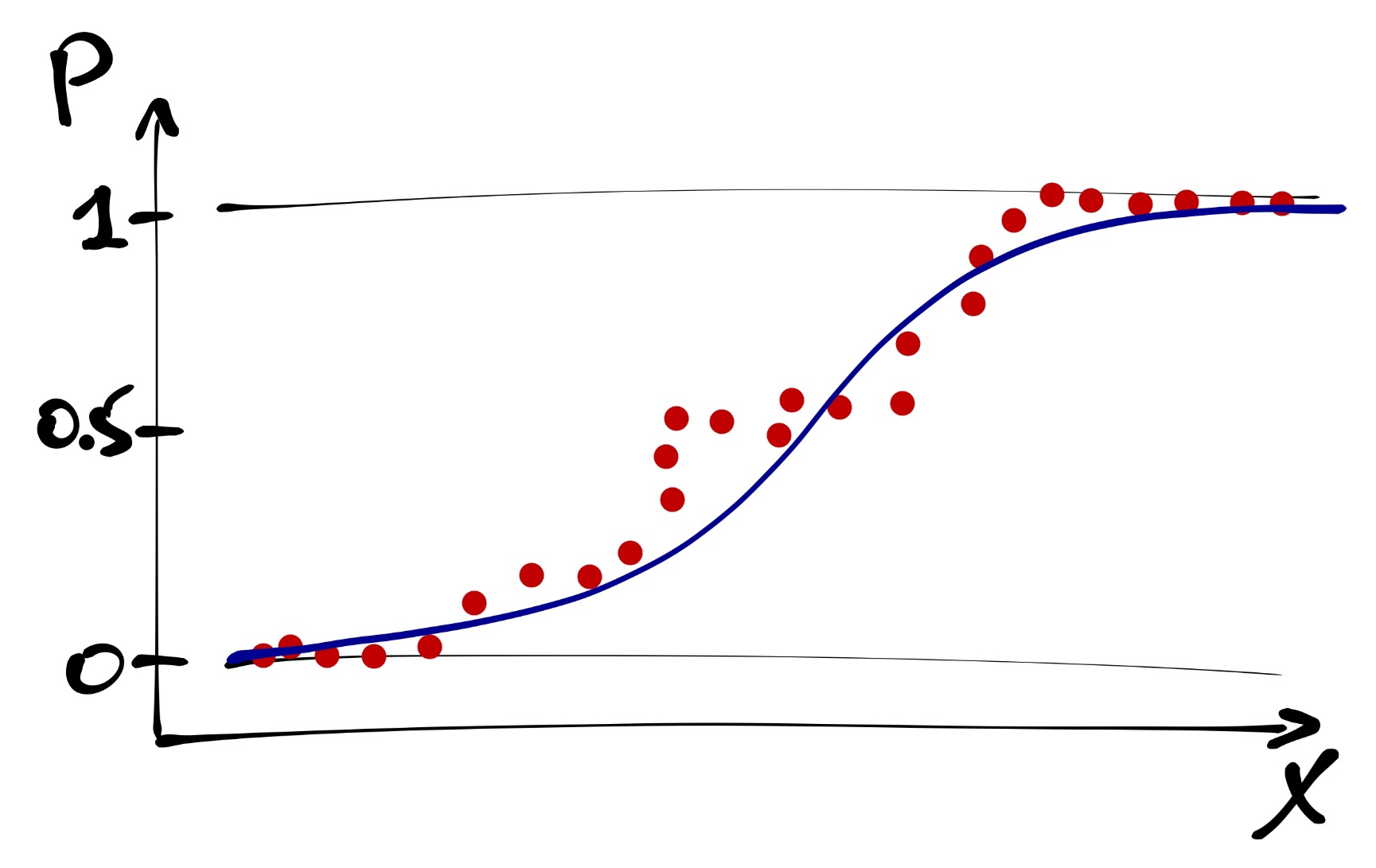
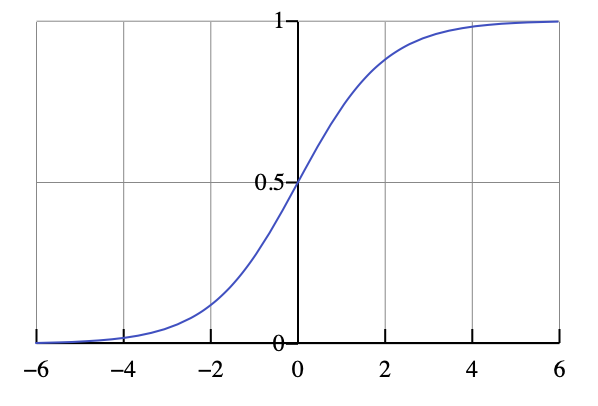
Она лежит как раз в пределах от 0 до 1. Наша логистическая кривая задается уравнением

\[p_i = \frac{e^{\beta_0 + \beta_1 x_i}}{1 + e^{\beta_0 + \beta_1 x_i}}\]

Логистическую кривую мы больше никогда не увидим [печаль :(], но она используется внутри функций, которыми мы строим модель.

21.6.2 Шансы и логиты

Теперь нам надо побороться с ограниченностью логистической кривой. Для этого можно перейти от вероятностей к шансам.

Шанс (отношение шансов, odds, odds ratio) — это отношение вероятности успеха к вероятности неудачи. Их величина варьируется от \(0\) до \(+\infty\).

Уже лучше, но все еще не самый лучший вариант… Последний шаг, необходимый нам, чтобы все было хорошо, юзануть логарифм, который преобразуем шансы в логиты.

\[ \mathrm{logit}(p) = \ln\left(\frac{p_i}{1-p_i}\right) \]

Значения логитов — трансформированные оценки вероятностей события. Они варьируют от \(-\infty\) до \(+\infty\), симметричны относительно нуля, и их удобно брать в качестве зависимой переменной для построения модели. Кроме того, logit-преобразование еще и линеаризует логистическую кривую. Доказательство.

Функция, используемая для линеаризации связи между предиктором и зависимой переменной, называется связывающей функцией (linked function). Функция logit-преобразоввания — одна из нескольких связывающих функций, применяемых для анализа бинарных переменных отклика.

Итак, summary от всего, что было выше:

От дискретной оценки событий (0 и 1) переходим к оценке вероятностей.
Связь вероятностей с предиктором описывается логистической кривой.
Если при помощи функции связи перейти от вероятностей к логитам, то связь будет описываться прямой линией.
Параметры линейной модели для такой прямой можно оценить с помощью регрессионного анализа.

21.7 Формулирование модели в математическом виде

GLM с биномиальным распределением отклика

\[y_i \thicksim \mathrm{Bin}(n = 1, p_i) \\ \mathbb{E}(y_i) = p_i = \frac{e^{\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p}}{1 + e^{\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p}}\]

Функция связи (linked function): \[ \ln \left(\frac{p_i}{1 - p_i}\right) = \eta_i \\ \eta_i = \beta_0 + \beta_1 x_{1i} + \dots + \beta_p x_{pi} \]

Для перехода от логитов к вероятностям используется функция, обратная функции связи. В данном случае, логистическое преобразование: \[ p_i = \frac{e^{\eta_i}}{1 + e^{\eta_i}} \]

21.8 Подбор линейной модели

Для построения модели используется функция glm(). Синтаксически она очень похожа на lm(), но у неё есть дополнительный аргумент family, в который необходимо указать тип регрессии, которую мы собираемся использовать. Внутри указания типа можно указать функцию связи, с использвоание которой будет строиться модель.

model <- glm(lvl ~ ., managers, family = binomial(link = 'logit'))

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

summary(model)

## 
## Call:
## glm(formula = lvl ~ ., family = binomial(link = "logit"), data = managers)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.8626  -0.0897  -0.0800   0.0000   3.5607  
## 
## Coefficients:
##                      Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -22.08642    1.13159 -19.518  < 2e-16 ***
## qualification         1.55224    0.14058  11.042  < 2e-16 ***
## autonomy              0.18304    0.24017   0.762    0.446    
## subdiv_regulations   -0.08816    0.27523  -0.320    0.749    
## company_regulations   0.10685    0.21973   0.486    0.627    
## direct_juniors        8.86211    0.70679  12.539  < 2e-16 ***
## func_juniors          2.98508    0.26324  11.340  < 2e-16 ***
## income_influence      0.63992    0.16049   3.987 6.68e-05 ***
## error_cost           -0.04441    0.15745  -0.282    0.778    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3626.58  on 3209  degrees of freedom
## Residual deviance:  640.79  on 3201  degrees of freedom
## AIC: 658.79
## 
## Number of Fisher Scoring iterations: 8

Модель сошлась, все ровно, хотя нам R выдал предупреждение. Вызываем функцию summary(), чтобы посмотреть статистики модели. Вывод функции нам уже знаком, он аналогичен тому, с которым мы встречались, однако все-таки отличается некоторыми деталями.

Во-первых, нет F-статистики. Во-вторых, нет R². Это связано с тем, что алгоритм GLM не работает с дисперсией и суммой квадратов — модель подбирается методом максимального правдоподобия. Данный метод позволяет учесть разную форму распределений, которые мы можем моделировать с использованием GLM.

21.8.1 Метод максимального правдоподобия

Правдоподобие (likelihood) — способ измерить соответствие имеющихся данных тому, что можно получить при определенных значениях параметров модели. Оно представляет собой произведение вероятностей получения каждой из точек данных:

\[ L(\theta | \mathrm{data}) = \prod_{i=1}^n f(\mathrm{data}|\theta), \] где \(f(\mathrm{data}|\theta)\) — функция распределения с параметрами \(\theta\).

Параметры модели должны максимизировать значения [логарифма] правдоподобия, т.е. \[ L(\theta | \mathrm{data}) \rightarrow \max \] Однако для упрощения вычислений используют логарифмы правдоподобий (loglikelihood) и максимизируют их \[ \ln L(\theta | \mathrm{data}) \rightarrow \max \] Аналитически такие задачи решаются редко, чаще используются методы численной оптимизации.

21.9 Анализ модели

Итак, продолжим изучать аутпут функции summary(). Обратимся к ней еще раз.

summary(model)

## 
## Call:
## glm(formula = lvl ~ ., family = binomial(link = "logit"), data = managers)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.8626  -0.0897  -0.0800   0.0000   3.5607  
## 
## Coefficients:
##                      Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -22.08642    1.13159 -19.518  < 2e-16 ***
## qualification         1.55224    0.14058  11.042  < 2e-16 ***
## autonomy              0.18304    0.24017   0.762    0.446    
## subdiv_regulations   -0.08816    0.27523  -0.320    0.749    
## company_regulations   0.10685    0.21973   0.486    0.627    
## direct_juniors        8.86211    0.70679  12.539  < 2e-16 ***
## func_juniors          2.98508    0.26324  11.340  < 2e-16 ***
## income_influence      0.63992    0.16049   3.987 6.68e-05 ***
## error_cost           -0.04441    0.15745  -0.282    0.778    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3626.58  on 3209  degrees of freedom
## Residual deviance:  640.79  on 3201  degrees of freedom
## AIC: 658.79
## 
## Number of Fisher Scoring iterations: 8

Мы видим знакомую нам табличку с оценками коэффициентов. У каждого предиктора есть информация о значении коэффициента при нем (Estimate), значение стандартной ошибки, z-value и p-value, рассчитанный для последнего.

Судя по аутпуту, значимыми являются следующие предикторы: профессиональная квалификация, количество прямых и функциональных подчинённых и влияние на доход компании. Заметьте, что в этой модели значимых предикторов меньше, чем в модели обычной линейной регрессии. Но так ли это?

Внимательно посмотрим на эту табличку. Раньше у нас были значения t-статистики — теперь z-теста. К чему это может приводить?

Чтобы ответить на этот вопрос, надо разобраться, что такое этот z-тест.

Значение z-value является результатом подсчета теста Вальда и позволяет оценить значимость коэффициента модели. Расчет статистики похож на подсчет t-теста, только распределение данной статистики ассимптотически стремиться к нормальному (отсюда и z). Ассимптотика приводит к тому, что опеределение значимости коэффициентов на маленьких выборках будет неточным.

\[ H_0: \beta_k = 0 \\ H_1: \beta_k \neq 0 \\ \\ z = \frac{b_k - \beta_k}{SE_{b_k}} = \frac{b_k}{SE_{b_k}} \thicksim \mathcal{N}(0,\,1) \]

Поскольку значения теста Вальда нам не могут обеспечить достаточной точности оценки коэффициентов, нам необходимы другие метрики оценки значимости коэффициентов.

21.10 Анализ девиансы и упрощение модели

Для получения более точных оценок необходимо поработать в логарифмами правдоподобий. Вообще логарифмы правдоподобий используются в GLM много для чего:

для описания качества подгонки модели;
для тестирования значимости подобранной модели в целом;
для тестирования значимости отдельных предикторов;
для отбора моделей.

Дла понимания механики анализа нам потребуется несколько полезных абстракций:

Насыщенная модель (saturated model) — каждое уникальное наблюдение (сочетание предикторов) описывается одним из \(n\) параметров.

\[ \ln L_{\mathrm{sat}} = 0 \\ \mathrm{df}_{\mathrm{sat}} = n - p_{\mathrm{sat}} = n - n = 0 \]

Нулевая модель (null model) — все наблюдения описываются одним параметром (средним значением)

\[ \hat y_i = \beta_0 \\ \ln L_{\mathrm{null}} \neq 0 \rightarrow -\infty \\ \mathrm{df}_{\mathrm{null}} = n - p_{\mathrm{null}} = n - 1 \]

Наша реальная (предложенная) модель, которую мы подбираем, будет находится где-то между насыщенной и нулевой моделью (вернее, не сама модель, а значение логарифма её правдоподобия).

\[ \hat y_i = \beta_0 + \beta_1 x_{1i} + \dots + \beta_p x_{pi} \\ \ln L_{\mathrm{model}} \neq 0 \\ \mathrm{df}_\mathrm{model} = n - p_\mathrm{model} \]

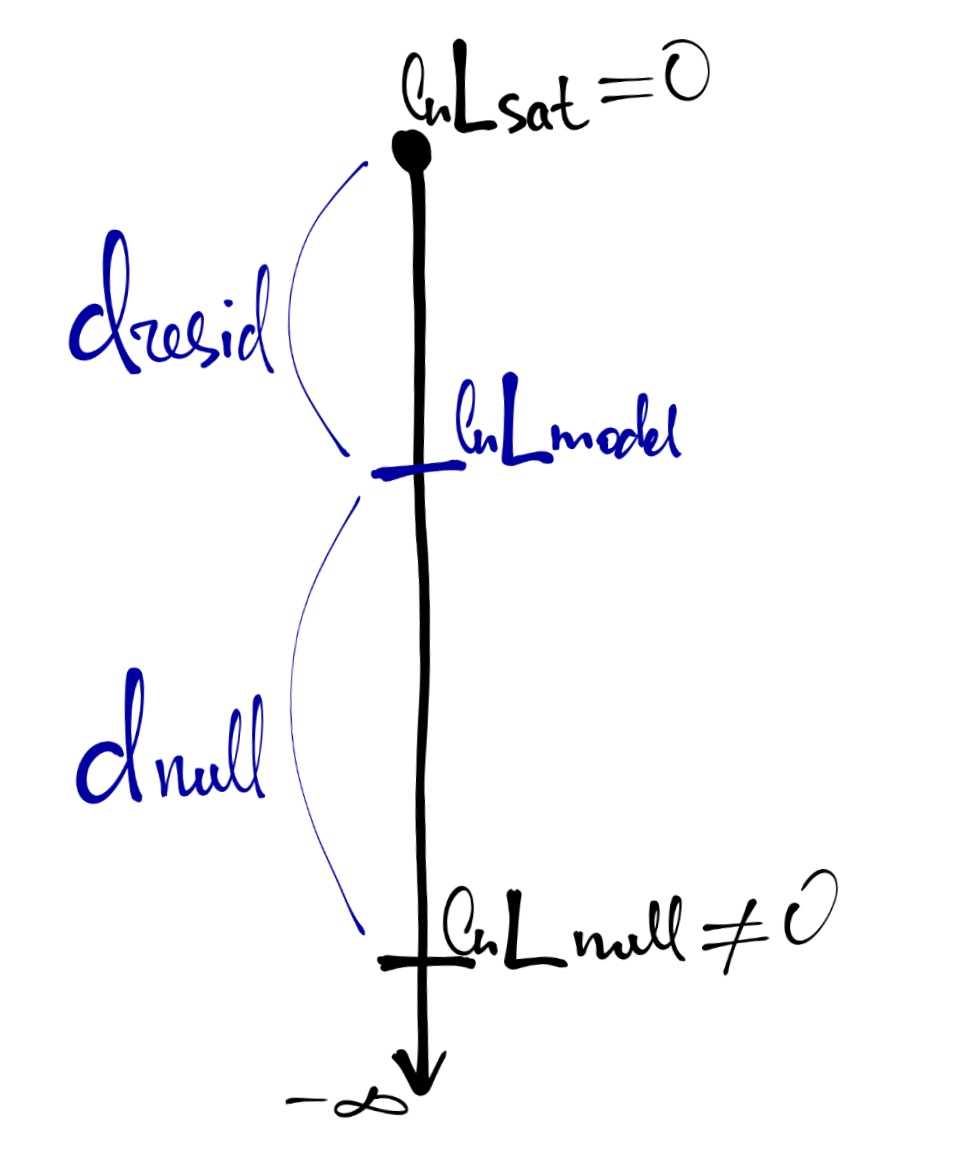
Девианса является мерой различия правдоподобий двух моделей (оценка разницы логарифмов правдоподобий). [см. рисунок выше]

Остаточная девианса \[ d_\mathrm{resid} = 2\big(\ln L_\mathrm{sat} - \ln L_\mathrm{model} \big) = -2 \ln(L_\mathrm{model}) \]

Нулевая девианса \[ d_\mathrm{null} = 2 \big(\ln L_\mathrm{sat} - \ln L_\mathrm{null}\big) = -2 \ln(L_\mathrm{null}) \]

Сравнение нулевой и остаточной девианс позволяет судить о статистической значимости модели в целом. Такое сравнение проводится с помощью теста отношения правдоподобий (likelihood ratio test, LRT).

\[ d_\mathrm{null} - d_\mathrm{resid} = -2 ( \ln L_\mathrm{null} - \ln L_\mathrm{model} ) = 2 (\ln L_\mathrm{model} - \ln L_\mathrm{null}) = 2 \ln \left( \frac{L_\mathrm{model}}{L_\mathrm{null}} \right) \\ \mathrm{LRT} = 2 \ln \left( \frac{L_\mathrm{M_1}}{L_\mathrm{M_2}} \right) = 2 (\ln L_\mathrm{M_1} - \ln L_\mathrm{M_2}), \] где \(M_1,\, M_2\) — вложенные модели (\(M_1\) — более полная, \(M_2\) — уменьшенная), \(L_\mathrm{M_1}, \, L_\mathrm{M_2}\) — правдоподобия.

Распределенеи разницы логарифмов правдоподобий аппроксиммируется распределением \(\chi^2\) с числом степеней свободы \(\mathrm{df} = \mathrm{df}_\mathrm{M_2} - \mathrm{df}_\mathrm{M_1}\).

LRT для тестирования значимости модели в целом:

\[ \mathrm{LRT} = 2 \ln \left( \frac{L_\mathrm{model}}{L_\mathrm{null}} \right) = 2 (\ln L_\mathrm{model} - \ln L_{\mathrm{null}}) = d_\mathrm{null} - d_\mathrm{resid} \\ \mathrm{df} = p_\mathrm{model} - 1 \]

LRT для тестирования значимости отдельных предикторов:

\[ \mathrm{LRT} = 2 \ln \left( \frac{L_\mathrm{model}}{L_\mathrm{reduced}} \right) = 2 (\ln L_\mathrm{model} - \ln L_\mathrm{reduced}) \\ \mathrm{df} = p_\mathrm{model} - p_\mathrm{reduced} \]

Реализуем изученное в R.

Протестируем значимость модели в целом. Для этого неоходимо создать нулевую модель с одним предиктором — среднее — и передать эту модель и тестируемую в функцию anova() с указанием параметра test = 'Chi'. Получим нужным нам аутпут:

model_null <- glm(lvl ~ 1, managers, family = binomial(link = 'logit'))
anova(model_null, model, test = 'Chi')

## Analysis of Deviance Table
## 
## Model 1: lvl ~ 1
## Model 2: lvl ~ qualification + autonomy + subdiv_regulations + company_regulations + 
##     direct_juniors + func_juniors + income_influence + error_cost
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1      3209     3626.6                          
## 2      3201      640.8  8   2985.8 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Как можно увидеть, наша модель получилась статистически значима.

Для тестирования значимости отдельных предикторов можно (и лучше) использовать функцию Anova() из пакета car.

Anova(model)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Analysis of Deviance Table (Type II tests)
## 
## Response: lvl
##                     LR Chisq Df Pr(>Chisq)    
## qualification         159.68  1  < 2.2e-16 ***
## autonomy                0.58  1     0.4477    
## subdiv_regulations      0.10  1     0.7484    
## company_regulations     0.24  1     0.6273    
## direct_juniors        536.45  1  < 2.2e-16 ***
## func_juniors          151.00  1  < 2.2e-16 ***
## income_influence       16.33  1   5.31e-05 ***
## error_cost              0.08  1     0.7778    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Мы получаем табличку, похожую на результат работы summary(), но с другими статистиками.

У нас есть незначимые предикторы, а значит можно упростить модель:

model1 <- update(model, . ~ . -error_cost)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

drop1(model1, test = 'Chi')

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Single term deletions
## 
## Model:
## lvl ~ qualification + autonomy + subdiv_regulations + company_regulations + 
##     direct_juniors + func_juniors + income_influence
##                     Df Deviance     AIC    LRT  Pr(>Chi)    
## <none>                   640.87  656.87                     
## qualification        1   801.72  815.72 160.85 < 2.2e-16 ***
## autonomy             1   641.40  655.40   0.53    0.4677    
## subdiv_regulations   1   641.00  655.00   0.13    0.7184    
## company_regulations  1   641.12  655.12   0.25    0.6172    
## direct_juniors       1  1178.48 1192.48 537.61 < 2.2e-16 ***
## func_juniors         1   798.65  812.65 157.78 < 2.2e-16 ***
## income_influence     1   659.39  673.39  18.52 1.684e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

model2 <- update(model1, . ~ . -subdiv_regulations)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

drop1(model2, test = 'Chi')

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Single term deletions
## 
## Model:
## lvl ~ qualification + autonomy + company_regulations + direct_juniors + 
##     func_juniors + income_influence
##                     Df Deviance     AIC     LRT  Pr(>Chi)    
## <none>                   641.00  655.00                      
## qualification        1   816.86  828.86  175.86 < 2.2e-16 ***
## autonomy             1   641.52  653.52    0.51    0.4735    
## company_regulations  1   641.15  653.15    0.15    0.7009    
## direct_juniors       1  1699.35 1711.35 1058.34 < 2.2e-16 ***
## func_juniors         1   798.89  810.89  157.89 < 2.2e-16 ***
## income_influence     1   660.24  672.24   19.23 1.157e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

model3 <- update(model2, . ~ . -company_regulations)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

drop1(model3, test = 'Chi')

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Single term deletions
## 
## Model:
## lvl ~ qualification + autonomy + direct_juniors + func_juniors + 
##     income_influence
##                  Df Deviance     AIC     LRT  Pr(>Chi)    
## <none>                641.15  653.15                      
## qualification     1   827.03  837.03  185.88 < 2.2e-16 ***
## autonomy          1   641.78  651.78    0.63    0.4286    
## direct_juniors    1  1703.82 1713.82 1062.67 < 2.2e-16 ***
## func_juniors      1   799.70  809.70  158.54 < 2.2e-16 ***
## income_influence  1   660.39  670.39   19.24 1.152e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

model4 <- update(model3, . ~ . -autonomy)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

drop1(model4, test = 'Chi')

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Single term deletions
## 
## Model:
## lvl ~ qualification + direct_juniors + func_juniors + income_influence
##                  Df Deviance     AIC     LRT  Pr(>Chi)    
## <none>                641.78  651.78                      
## qualification     1  1037.93 1045.93  396.15 < 2.2e-16 ***
## direct_juniors    1  1708.43 1716.43 1066.65 < 2.2e-16 ***
## func_juniors      1   833.76  841.76  191.98 < 2.2e-16 ***
## income_influence  1   662.32  670.32   20.54 5.845e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Anova(model4)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

## Analysis of Deviance Table (Type II tests)
## 
## Response: lvl
##                  LR Chisq Df Pr(>Chisq)    
## qualification      396.15  1  < 2.2e-16 ***
## direct_juniors    1066.65  1  < 2.2e-16 ***
## func_juniors       191.98  1  < 2.2e-16 ***
## income_influence    20.54  1  5.845e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

В модели остались только значимые предикторы, и таким образом, мы получили нашу финальную модель.

Кроме статистический тестов для сравнения моделей можно использовать информационные критерии. Например, информационный критерий Акаике (Akaike information criterion), позволяющий сделать выбор из нескольких моделей. Его можно использовать и в нашем случае как дополнительную проверку.

AIC(model, model4)

##        df      AIC
## model   9 658.7949
## model4  5 651.7787

С удалением незначимых предикторов из модели AIC хоть и немного, но снизился, что позволяет сделать вывод о том, что модель с меньшим количеством предикторов лучше, чем модель, включающая все предложенные предикторы.

21.11 Интерпретация коэффициентов модели

Еще раз позовем summary нашей окончательной модели:

summary(model4)

## 
## Call:
## glm(formula = lvl ~ qualification + direct_juniors + func_juniors + 
##     income_influence, family = binomial(link = "logit"), data = managers)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.8408  -0.0852  -0.0852   0.0000   3.5391  
## 
## Coefficients:
##                  Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      -22.0070     1.1112 -19.804  < 2e-16 ***
## qualification      1.6056     0.1112  14.441  < 2e-16 ***
## direct_juniors     8.8192     0.6459  13.653  < 2e-16 ***
## func_juniors       3.0718     0.2423  12.680  < 2e-16 ***
## income_influence   0.6440     0.1458   4.418 9.97e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3626.58  on 3209  degrees of freedom
## Residual deviance:  641.78  on 3205  degrees of freedom
## AIC: 651.78
## 
## Number of Fisher Scoring iterations: 9

Что значат эти непонятные коэффициенты при предикторах? В общих линейных моделях все ясно как белый день, а тут какая-то дичь…

Посмотрим на математическую запись нашей модели:

\[ \mathrm{Out}_i \thicksim \mathrm{Bin}(n = 1, \, p_i) \\ \mathbb{E}(\mathrm{Out}_i) = p_i \\ \ln \left(\frac{p_i}{1 - p_i}\right) = \eta_i \\ \eta_i = -22.0 + 1.6 \, \mathrm{qualification}_i + 8.8 \, \mathrm{direct\_juniors}_{i} + 3.1 \, \mathrm{func_juniors}_i + 0.6 \, \mathrm{income_influence}_i \]

Наша зависимая переменная — логарифм отношения шансов. От этого и будем толкаться.

Тогда,

\(b_0\), интерсепт, показывает логарифм отношения шансов для случая, когда все остальные предикторы равны нулю — в данном примере он сложноинетерпретабелен;
\(b_j\) показывает, на сколько единиц изменяется логарифм отношения шансов при изменении значения предиктора на единицу.

Корректно, но непонятно… Чтобы разобраться лучше, немного потупим в алгебру.

21.11.1 Немного алгебры для понимания сути коэффициентов

Пусть у нас есть модель с одним непрервным предиктором. Тогда она будет записываться так:

\[ \eta = b_0 + b_1 x \]

В терминах логитов её можно записать следующим образом:

\[ \eta = \ln \left( \frac{p}{1 - p} \right) = \ln (\mathrm{odds}) \]

Как изменится предсказание модели при изменении предиктора на единицу?

\[ \eta_{x+1} - \eta_x = \ln (\mathrm{odds}_{x+1}) - \ln (\mathrm{odds}_{x}) = \ln \left( \frac{\mathrm{odds}_{x+1}}{\mathrm{odds}_x} \right) \] \[ \eta_{x+1} - \eta_x = b_0 + b_1 (x + 1) - b_0 - b_1x = b_1 \] \[ \ln \left( \frac{\mathrm{odds}_{x+1}}{\mathrm{odds}_{x}} \right) = b_1 \] \[ \frac{\mathrm{odds}_{x+1}}{\mathrm{odds}_{x}} = e^{b_1} \]

Таким образом, \(e^{b_1}\) показывает, во сколько раз изменится отношение шансов при увеличении предиктора на единицу. Для дискретных предикторов \(e^{b_1}\) покажет, во сколько раз различается отношение шансов для данного уровня предиктора по сравнению с базовым.

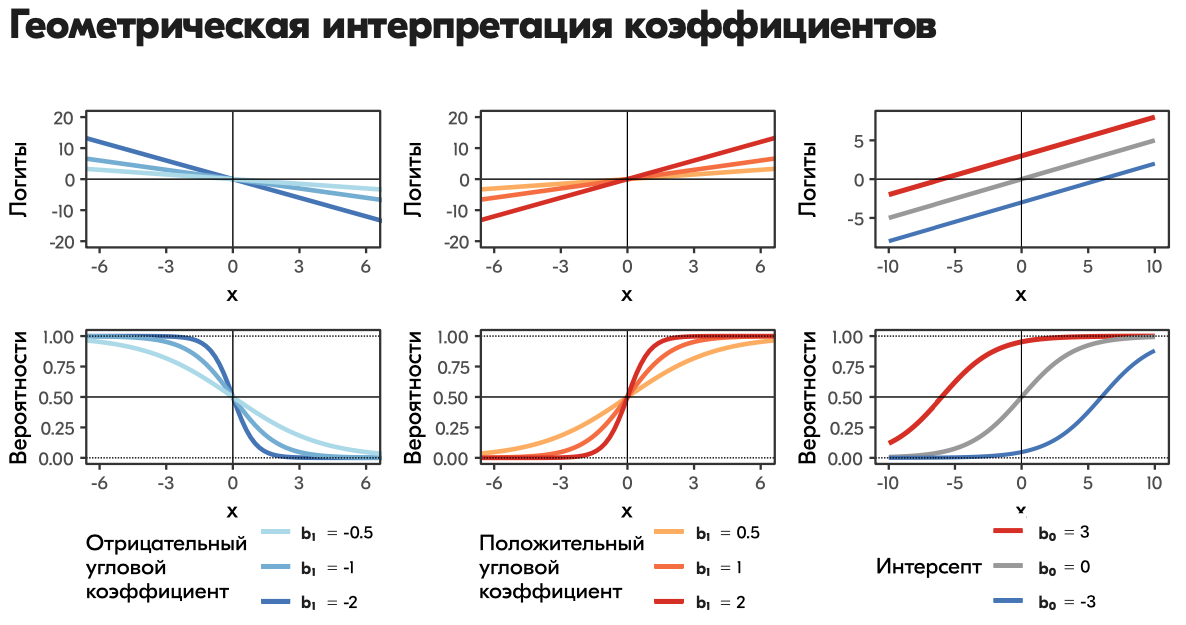
Теперь мы можем тракровать полученные коэффициенты нормальным языком.

\[ \eta_i = -22.0 + 1.6 \, \mathrm{qualification}_i + 8.8 \, \mathrm{direct\_juniors}_{i} + 3.1 \, \mathrm{func\_juniors}_i + 0.6 \, \mathrm{income\_influence}_i \]

При увеличении оценки профессиональной квалификации на 1 отношение шансов принадлежать к уровню менеджеров увеличится в \(e^{3.1} = 22.2\) раза. То есть работник, имеющий более высокую оценку профессиональной квалицикации, имеет больше шансов быть менеджером.

Потренируйтесь в интерпретации коэффициентов при предикторах самостоятельно. Ешё раз изучите логику интерпретации и сформулируйте, как связаны предикторы direct_juniors, func_juniors и income_influence с целевой переменной модели.

21.12 Предсказательная сила модели

Оценить предсказательную силу общих линейных моделей не сложно, и логика процесса интуитивно понятна. С логистической моделью же есть некоторые тонкости.

Чтобы оценить предсказательную силу модели, нам потребуется разбить наши данные на две подвыборки — обучающую и тестовую¹. Первую мы использует для подбора коэффициентов модели, а вторую для проверки предсказательной силы.

set.seed(5432)
ind_train <- sample(1:nrow(managers), size = 0.7 * nrow(managers), replace = FALSE)
managers %>% 
  slice(ind_train) -> managers_train
managers %>% 
  slice(-ind_train) -> managers_test

Обучим модель, то есть подберём коэффициенты, на тренировочных данных. Возьмём полную модель.

model5 <- glm(lvl ~ ., managers_train, family = binomial)

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

Как оценить, насколько модель хорошо работает? Для этого потребуются метрики качества модели. Однако перед этим надо поработать с предсказаниями.

21.12.1 Перевод непрерывных предсказаний в дискретные

Множество допустимых значений нашей целевой переменной — \(\{0, 1\}\), а наша модель возвращает вероятности принадлежности каждого из наблюдений к классу 1:

head(model5$fitted.values)

##            1            2            3            4            5            6 
## 0.9999609133 0.0048211719 0.0004782344 0.0634837569 0.0004782344 0.0048211719

Поэтому чтобы мы смогли рассчитать метрики качества, нам необходимо перейти от вероятностей обратно к нулям и единицам. Для этого необходимо выбрать порог — если значение вероятности выше него, мы будем считать, что модель предсказала 1, если ниже, то 0. Значение порога зависит от многих факторов и будет влиять на качество модели. Прежде всего стоит ориентироваться на сферу деятельности, в которой вы проводите анализ. Если у вас качественные чистые данные и вам важна высокая точность, то и порог для предсказаний должен быть высокий — \(\geq 0.9\). Если же вы знаете, что вы работаете с зашумлёнными данными, и цена ошибки не так высока, то можете выбрать более либеральный критерий — \(0.7-0.8\). Самый либеральный критерий из возможных — \(0.5\), что по сути есть вероятность случайного угадывания.

Итак, переведем предсказания пока на тренировочной выборке в дискретную форму. Выберем критерий \(0.8\) как не очень строгий, но и не очень либеральный:

predicted_train <- ifelse(predict(model5, type = 'response') > 0.8, 1, 0)

21.12.2 Confusion matrix

Построим confusion matrix — это таблица частот по модельным и реальным значениям нашей целевой переменной

table(managers_train$lvl, predicted_train)

##    predicted_train
##        0    1
##   0 1678    5
##   1   71  493

По столбцам идут предсказанные значения, по строкам — реальные. В целом мы видим, что модель практически всегда предсказывает верно, однако хотелось бы как-то понять, что такое это «практически всегда» в числовом формате.

Для этого надо понять структуру confusion matrix:

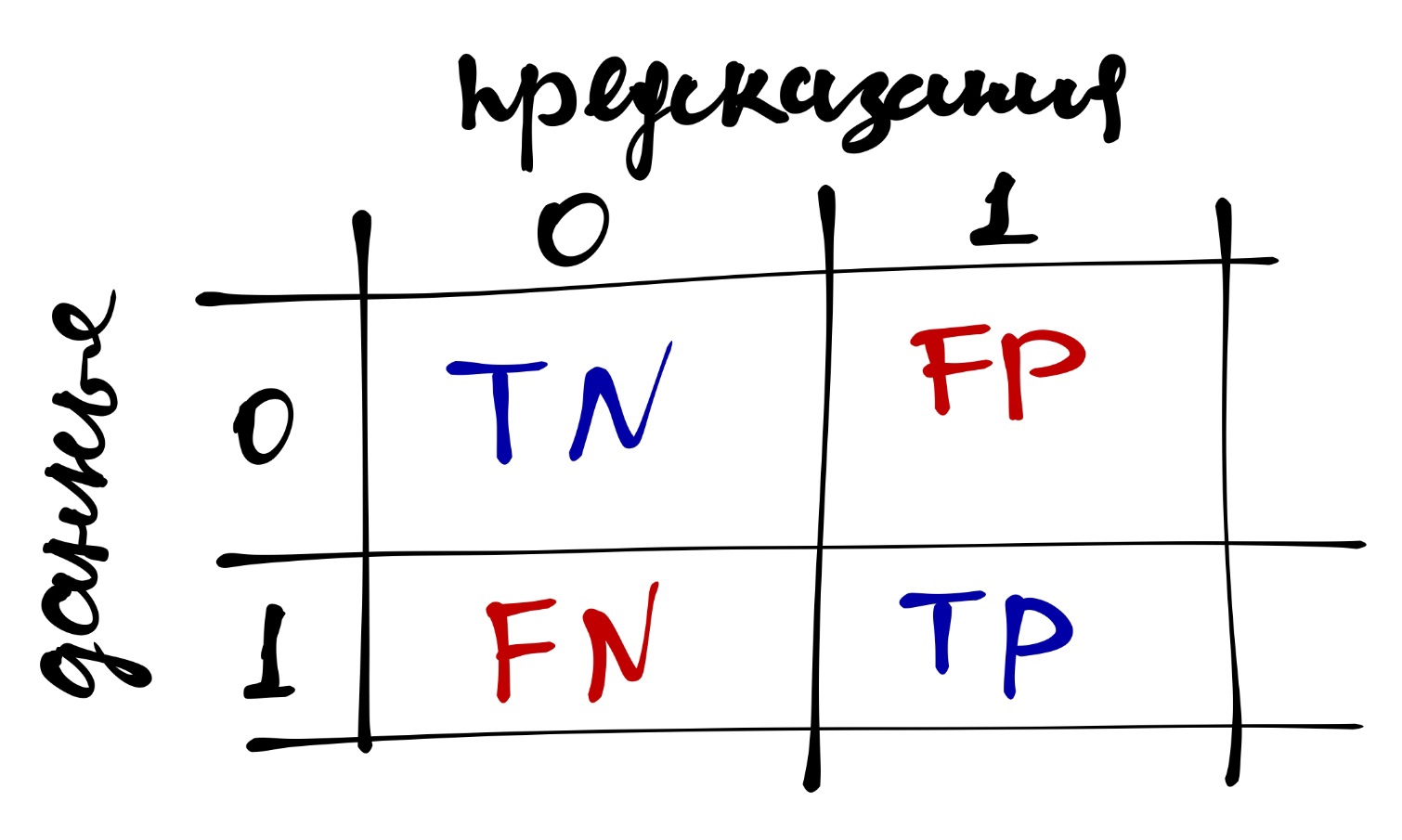
True Positive (\(TP\)) — верное предсказанные единицы
True Negative (\(TN\)) — верно предсказанные нули
False Positive (\(FP\)) — ложноположительные предсказания, ошибочно предсказанные единицы
False Negative (\(FN\)) — ложноотрицательные предсказания, ошибочно предсказанные нули

На основе данных значение можно расчитать несколько метрик качества модели.

21.12.3 Accuracy

Чаще всего эту метрику называют «точность». Она определяется по формуле

\[ \mathrm{accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \]

Она показывает долю верно предказанных значений.

Напишите фунцию, которая будет принимать на вход confusion matrix и возвращать значение accuracy.

confmat <- table(managers_train$lvl, predicted_train)

accuracy(confmat)

## [1] 0.9661771

Это неплохая метрика, но она перестаёт работать на несбалансированных данных. Например, у нас есть такие данные по целевой переменной (dv):

dv <- c(0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1)

Пусть у нас есть наиболее топорная модель, которая просто всегда предсказывает ноль:

pred <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)

Тогда точность будет следующая:

mean(dv == pred)

## [1] 0.7272727

Достаточно высокий показатель, хотя модель не ухватывает закономерность вовсе. Поэтому были разработаны другие метрики качества, которые хорошо работают и на несбалансированных данных.

21.12.4 Precision and Recall

Presicion тоже переводится как «точность», поэтому лучше пользоваться английской терминологией во избежании путаницы. Эта метрика показывается долю верно предсказанных единиц, то есть сколько из предсказанных единиц предсказано верно:

\[ \mathrm{precision} = \frac{TP}{TP + FP} \]

Напишите фунцию, которая будет принимать на вход confusion matrix и возвращать значение precision.

precision(confmat)

## [1] 0.9899598

Recall можно перевести как «полнота», хотя по сути это снова «точность». Эта метрика показывается долю предсказанных единиц из всех единиц датасета, то есть сколько из всех единиц датасета модель предсказала верно:

\[ \mathrm{recall} = \frac{TP}{TP + FN} \]

Напишите фунцию, которая будет принимать на вход confusion matrix и возвращать значение recall.

recall(confmat)

## [1] 0.8741135

И ещё раз обобщаюшая картинка:

Очевидно, что чем ближе показатели всех метрик к единице, тем качество модели выше.

21.12.5 F1-мера

На основе precision и recall вычисляется ещё одна метрика качества, которая является гармоническим средним этих двух метрик.

\[ \mathrm{F1} = 2 \times \frac{\mathrm{precision} \times \mathrm{recall}}{\mathrm{precision + \mathrm{recall}}} \]

Её значение также изменяется от нуля до единицы.

Опять?

Напишите фунцию, которая будет принимать на вход confusion matrix и возвращать значение F1-меры.

Подсказка

Можно использовать функции, написанные ранее, внутри новой функции.

F1(confmat)

## [1] 0.9284369

21.12.6 ROC-AUC

Ну и напоследок, самое занятное. Ещё одна метрика качества модели. Однако логика её расчёта не такая простая.

Чем хороша эта метрика? Тем, что она работает не с предсказанными значениями (0 и 1), а с предсказанными вероятностями. Таким образом, она избавляет нас от вмешательства нас же в предсказания, ведь когда мы выбираем порог, мы хотя и опираемся на какое-то содержательное основание, тем не менее, глобально выбираем его условно произвольно.

Что рассчитать значение этой метрики нужно сделать следующее (разберём на некотором вымышленном примере):

Упорядочить объекты по убыванию значения предсказанной вероятности:

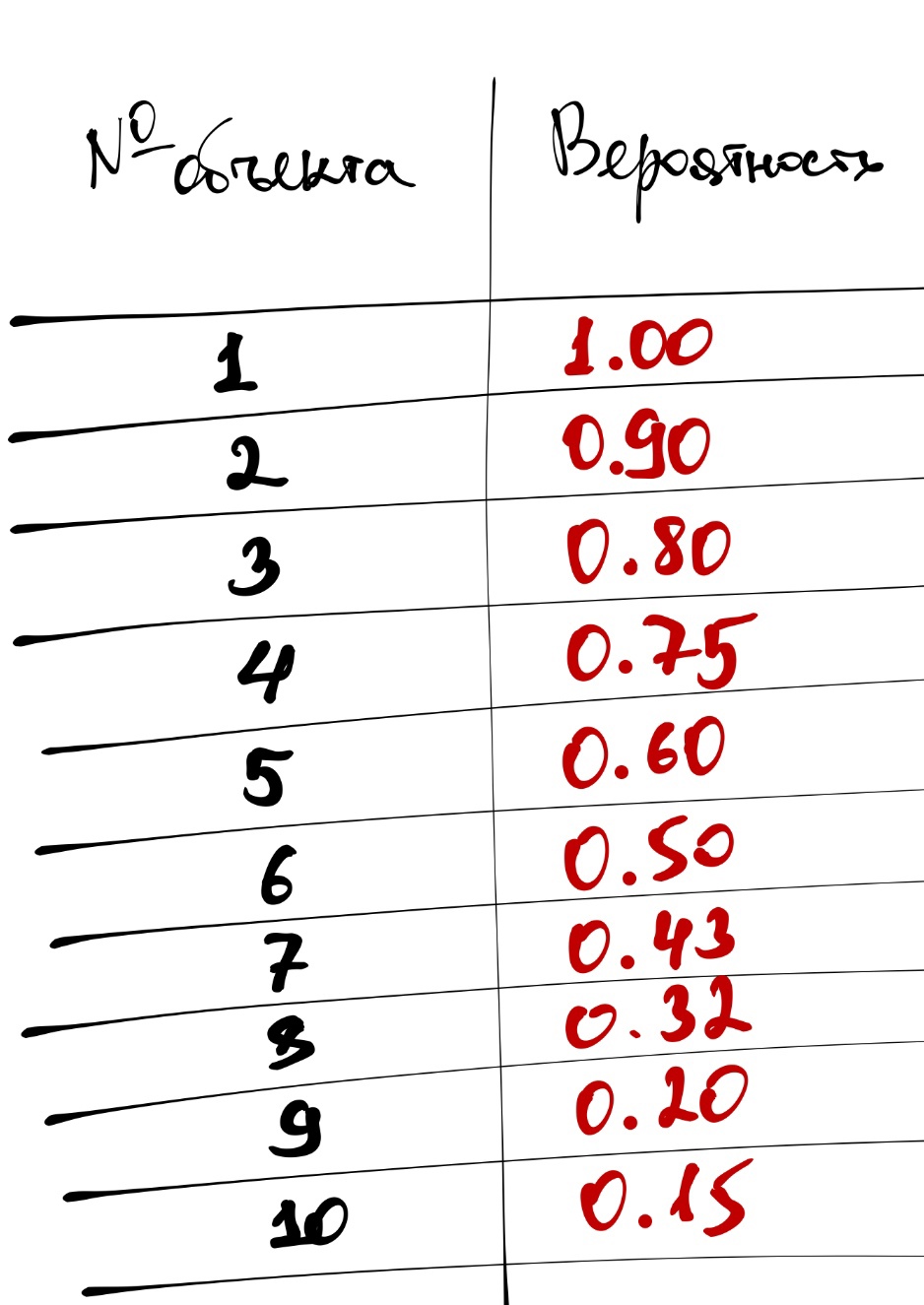
Добавить столбец истинных значений (0 и 1)

Отметим, что если модель идеально справляется с предказаниями, то в упорядоченном по значению предсказанной вероятности наборе данных сначала будут идти все наблюдения с истинным значением 1, а потом с 0.

Построим кривую, которая будет описывать качество нашей модели:

Стартуем из точки \((0, 0)\) и хотим прийти в точку \((1, 1)\):

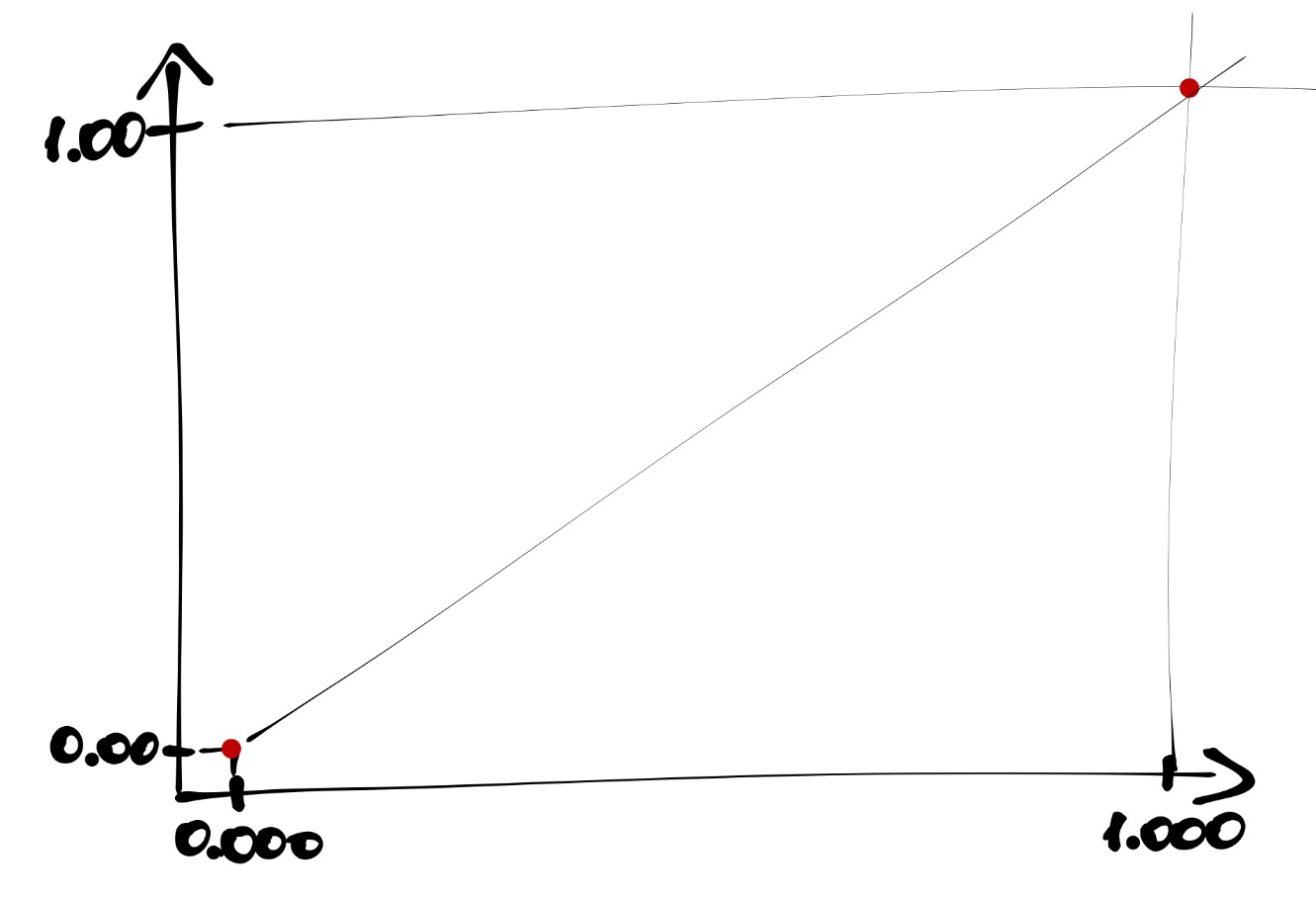
Ось \(y\) делим на равные части, число которых равно количеству 1 в датасете:

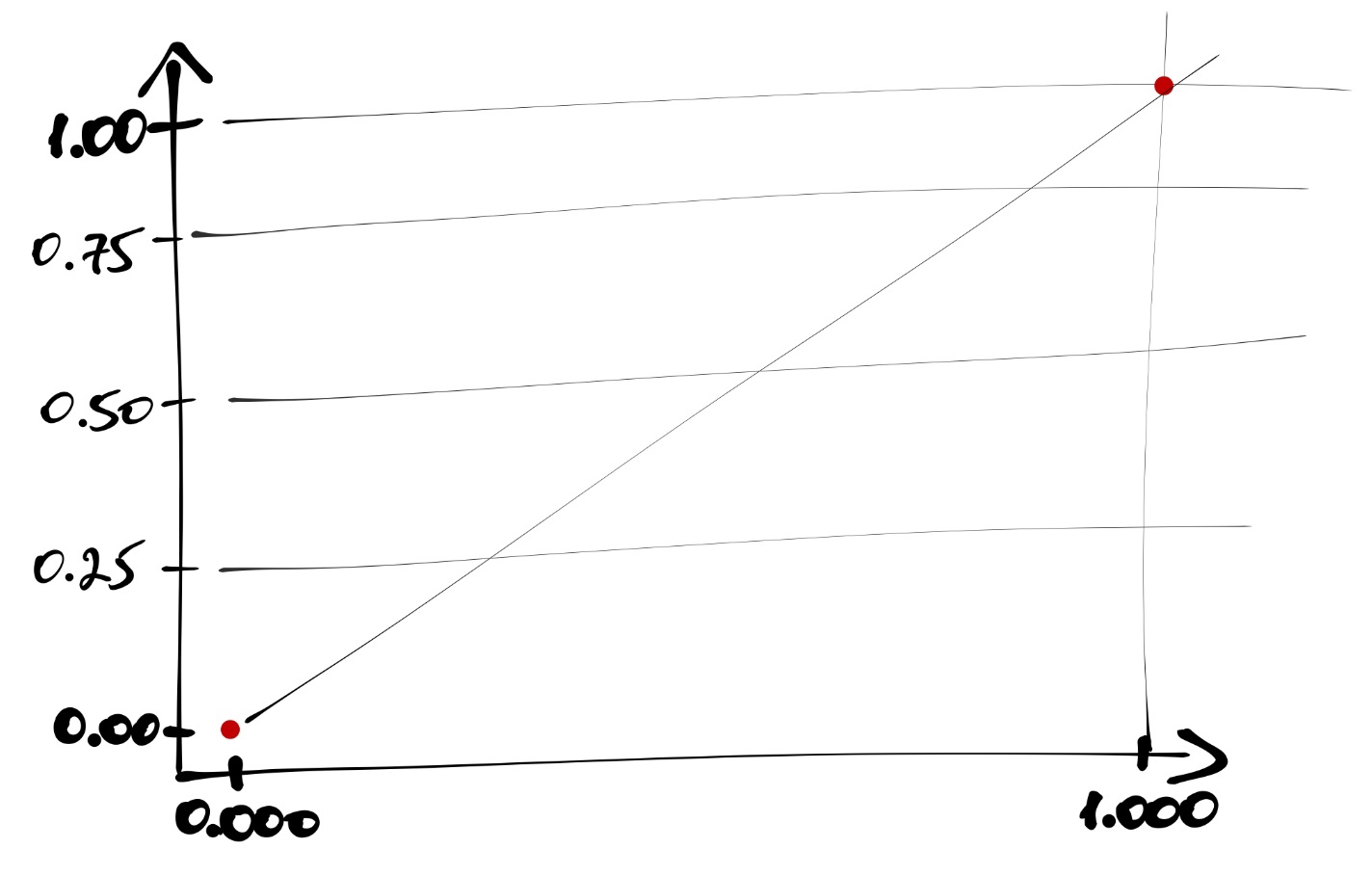
Ось \(x\) делим на равные части, число которых равно количеству 0 в датасете:

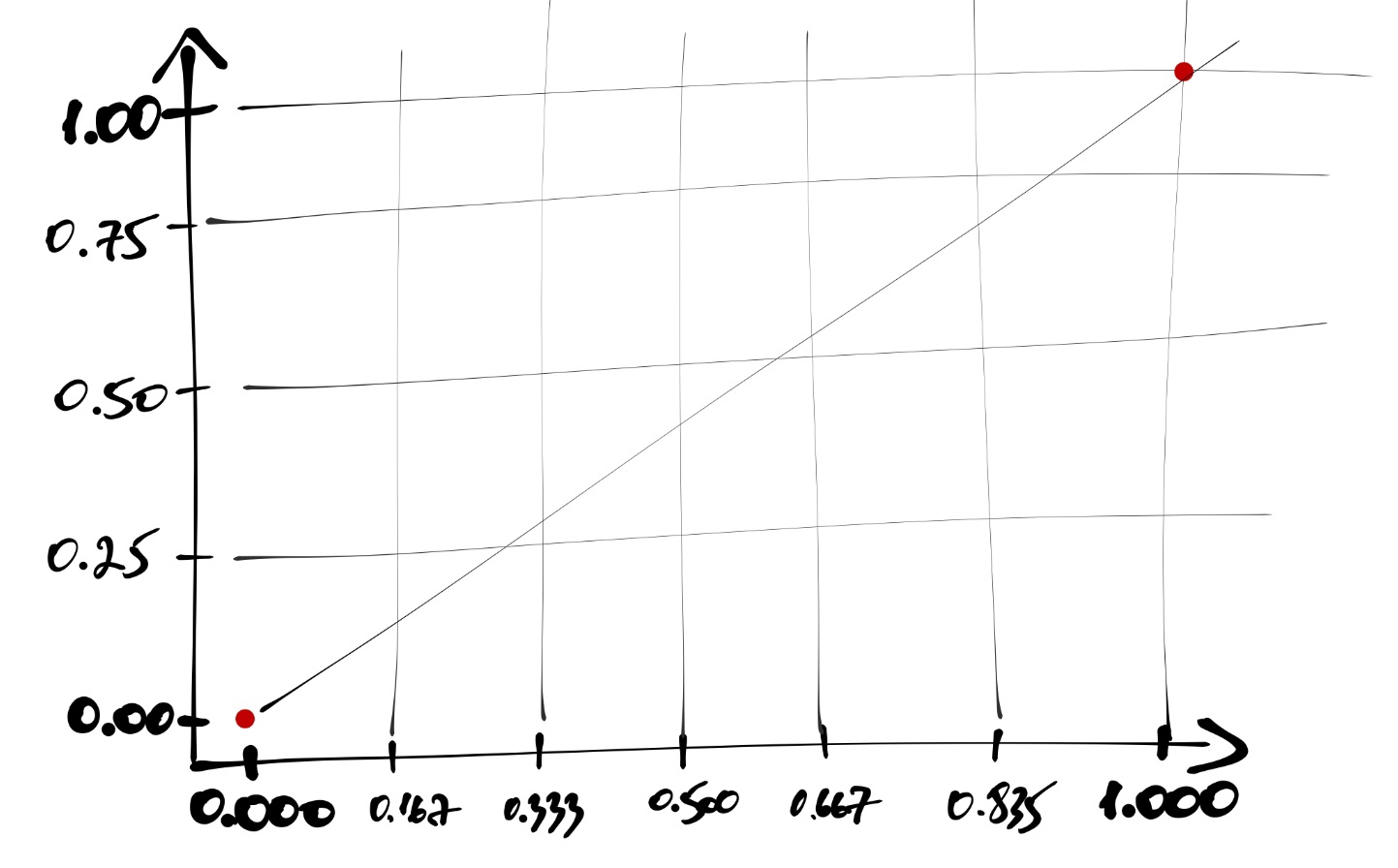
Идём по нашим данным сверху вниз, и когда встречаем наблюдение со значением 1, поднимаемся на графике на одно деление вверх; когда встречаем наблюдение со значением 0, сдвигаемся на одно деление вправо.
В итоге получится такая кривая:

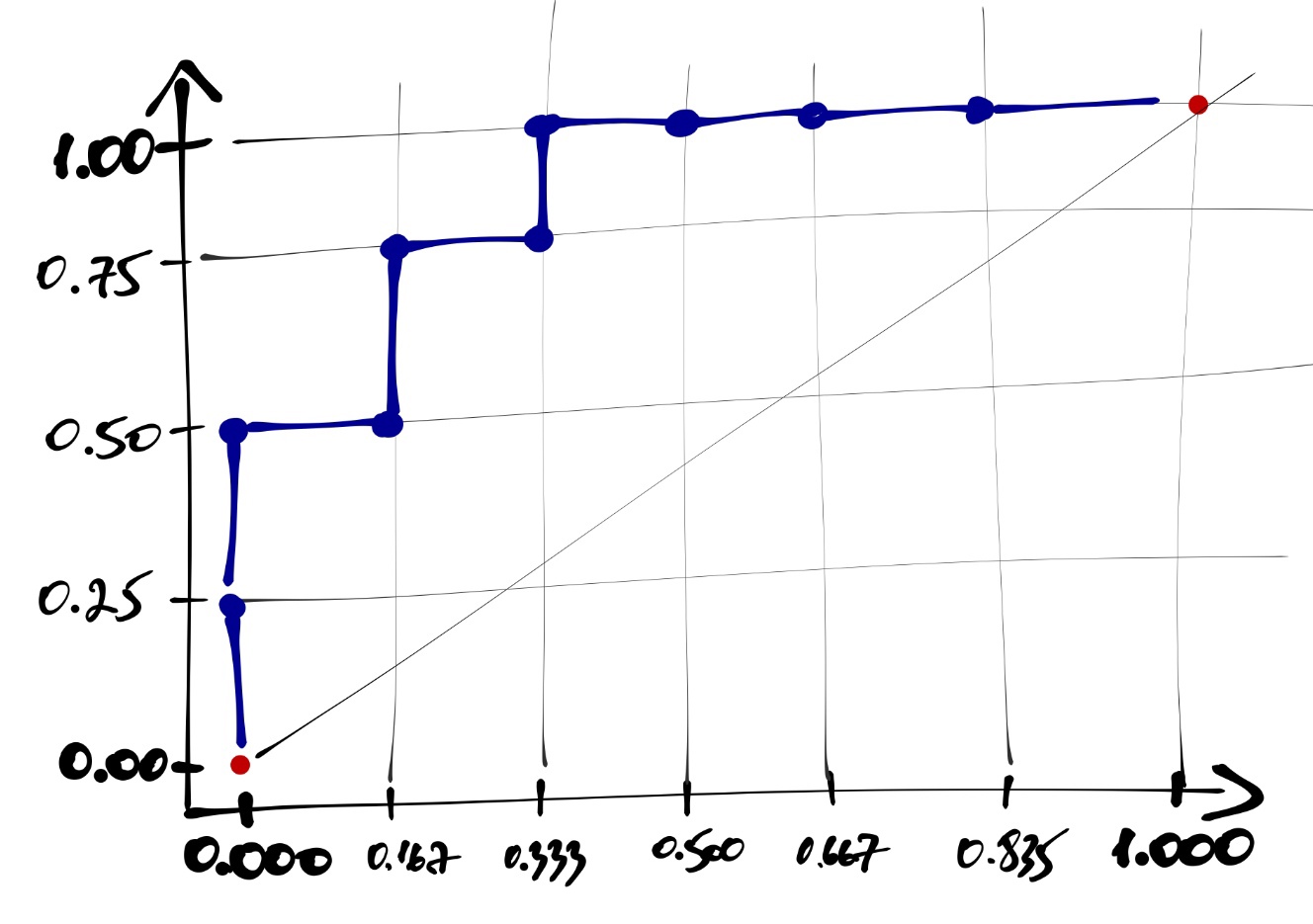
Каждая точка на этой кривой соответствует некоторому порогу вероятности отсечения объектов. Например, выделенная точка (рисунок ниже) соответствует порогу вероятности \(0.6\) и имеет координаты \((\frac{1}{6}, \frac{3}{4})\). Это означает, что если при переходе к предсказаниями модели мы будем использовать порог \(0.6\), то доля true positive, или true positive rate (TRP) окажется равной \(\frac{3}{4}\), а доля falce positive, или false positive rate (FPR) окажется равной \(\frac{1}{6}\).

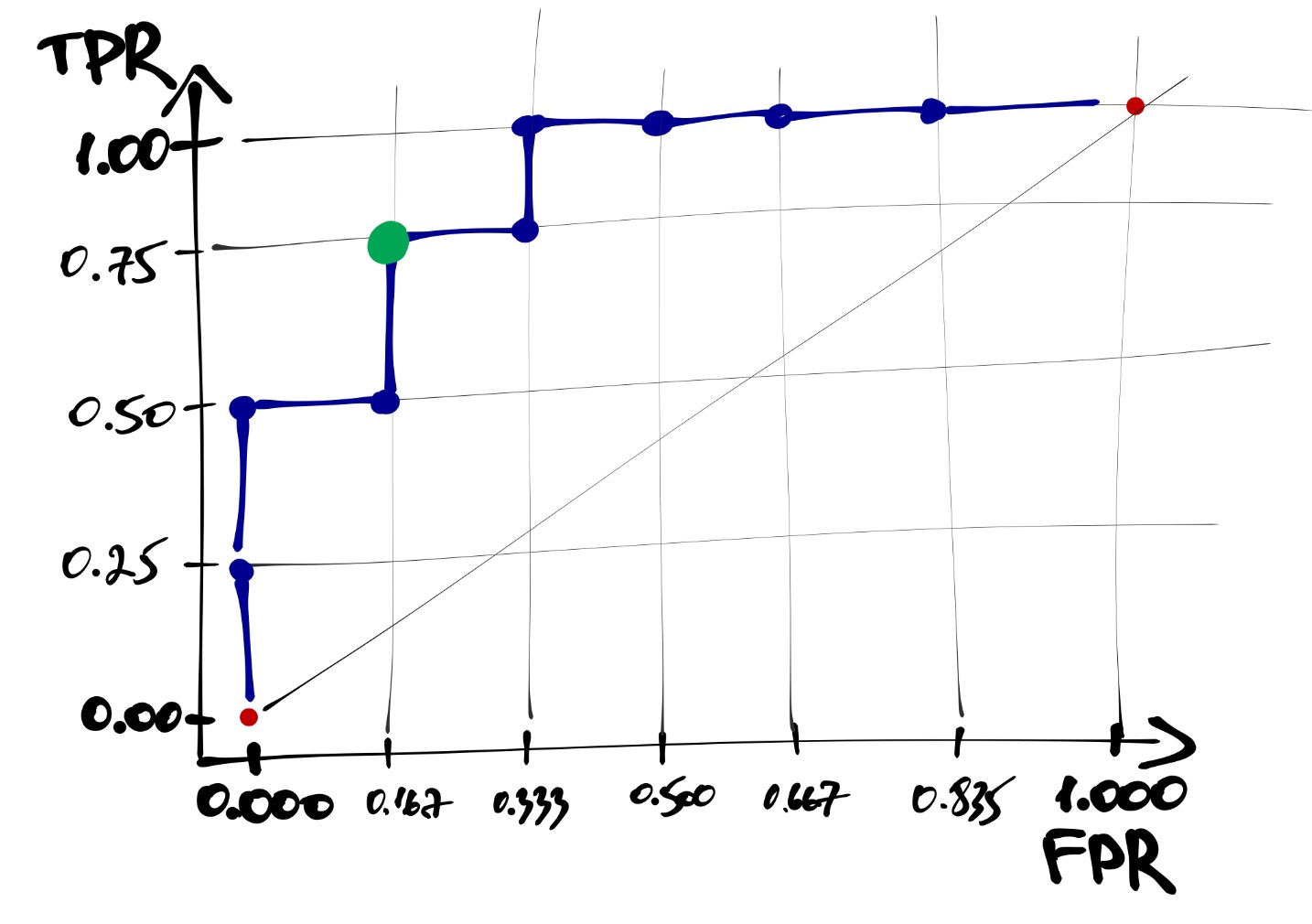
Построенная кривая называется ROC-кривой (receiver operating characteristic).

Определяем площадь фигуры под ROC-кривой — это и будет значением метрики ROC-AUC. AUC — area under a curve.

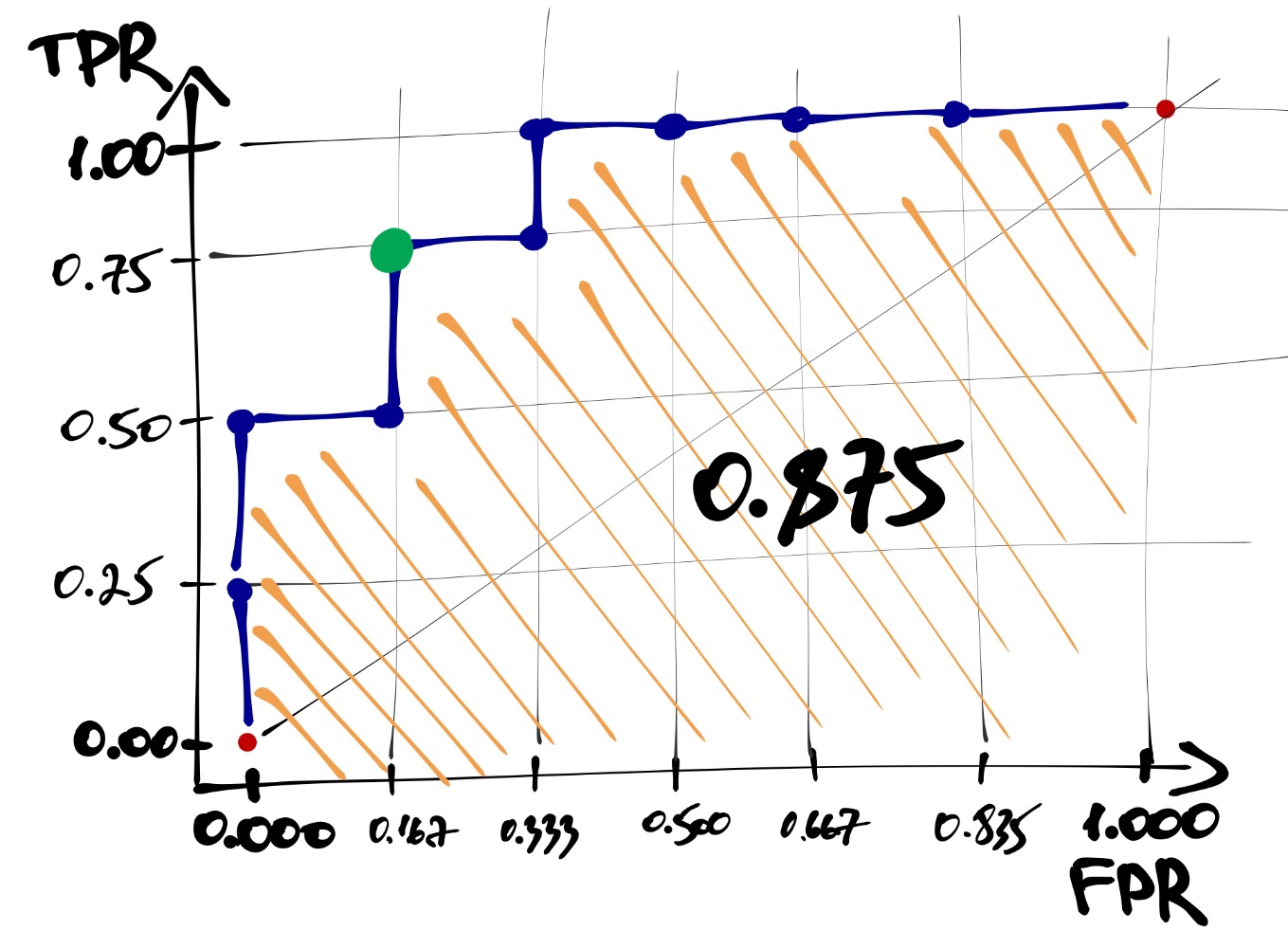
В случае идеального упорядочивания наблюдений по предсказанной вероятности площадь под кривой будет равна единице. Чем ближе значение ROC-AUC к единице, тем модель работает лучше. Значение \(0.5\) указывает на то, что модель совсем не ухватывает закономерность и точность её предсказаний на уровне случайного угадывания — ROC-кривая в этом случае будет проходить близко к диагонали \([(0,0),(1,1)]\).

В R эту метрику рассчитать с помощью функций roc() и auc() из пакета pROC. Первая функция хочет получить на вход вектор истинных значений и вектор предсказанных вероятностей. Вторая же хочет получить результат работы первой:

library(pROC)

## Type 'citation("pROC")' for a citation.

## 
## Attaching package: 'pROC'

## The following objects are masked from 'package:stats':
## 
##     cov, smooth, var

auc(roc(managers_train$lvl, model5$fitted.values)) # на тренировочных данных

## Setting levels: control = 0, case = 1

## Setting direction: controls < cases

## Area under the curve: 0.9834

21.13 Предсказания на новых данных

Мы рассчитали метрики качества на тренировочных данных, но гораздо интереснее, как модель справится с предсказаниями на тех данных, которые она ещё не видела. Это просто проверить.

predicted_test <- ifelse(predict(model5, managers_test, type = 'response') > 0.8, 1, 0)
cm <- table(managers_test$lvl, predicted_test)

Рассчитаем метрики качества и сравним со значениями для тренировочной выборки:

tibble(data = c('train', 'test'),
       accuracy = c(accuracy(confmat), accuracy(cm)),
       precision = c(precision(confmat), precision(cm)),
       recall = c(recall(confmat), recall(cm)),
       F1 = c(F1(confmat), F1(cm)))

## # A tibble: 2 x 5
##   data  accuracy precision recall    F1
##   <chr>    <dbl>     <dbl>  <dbl> <dbl>
## 1 train    0.966     0.990  0.874 0.928
## 2 test     0.977     0.987  0.923 0.954

Здесь надо обратить внимание на следующий очень важный момент: согласно метрикам качества, модель, пусть и немного, но лучше работает на тестовых данных, чем на тренировочных. Такого, вообще-то говоря, быть не может, и любая модель будет работать на тестовых данных хуже, чем на тех, на которых она была обучена. Это приводит нас с мысли, что результат работы модели зависит не от самой модели и её коэффициентов, а, скорее, от случайного совпадения данных — проще говоря, модель переобучилась. Мы вплотную подошли к сфере машинного обучения и дальше не пойдём, так как это не цель нашего курса. Но о самом феномене вы теперь знаете.

Машин лёрнинг, привет 👋↩