23 Регуляризация регрессии
Мы говорили о том, что частой проблемой при подборе модели линейной регрессии является мультиколлинеарность предикторов. Напомним, чем это чревато.
В случае абсолютно линейной связи коэффициент модели просто не вычислится — в аутпуте будет NA. Как правило, это намёк на то, чтобы проверить данные — возможно, у вас есть одна и та же переменная, записанная по-разному (например, рост в метрах и сантиметрах). В случае высоких (но меньших единицы) корреляций проблема подбора коэффициентов решается с помощью методов численной оптимизации, однако это может приводить к смещённым оценкам коэффициентов модели, а также большим ошибкам в оценках коэффициентов.
Поэтому с мультиколлинеарностью надо бороться. Мы уже обсуждали метод служебной регрессии. Теперь обсудим ещё один способ.
В ходе подбора модели мы получаем оценки коэффициентов модели \(\hat \beta_j = b_j\):
\[ \hat y_i = b_0 + b_1 x_{i1} + b_2 x_{i2} + \dots + b_p x_{ip} \]
В случае мультиколлинеарности оценки ряда коэффициентов могут быть завышены. Значит нужно их «штрафовать»! Вернее, не сами коэффициенты, а сумму квадратов ошибок модели:
\[ RSS + \text{штраф} \rightarrow \underset{\hat \beta}{\min} \]
Но штрафовать можно по-разному — и мы будем получать разные результаты.
23.1 Варианты штрафа
Штраф состоит из суммы оценок коэффициентов модели. Однако здесь снова та же проблема, что и с дисперсией — оценки могут быть как положительные, так и отрицательные, поэтому для того, чтобы их сумма не обнулилась, нужно каким-то образом избавиться от знака. Варианта как обычно два — поэтому мы получаем два способа подсчёта штрафа.
Напомним себе, что
\[ RSS = \sum_{i=1}^n (y_i - \hat y_i) \]
Мы можем взять квадраты коэффициентов модели, тогда получим следующее:
\[ \sum_{i=1}^n (y_i - \hat y_i) + \lambda \sum_{j=1}^p b_j^2 \rightarrow \underset{b}{\min} \]
Такой подход называется ridge-регрессия.
Мы можем взять модули коэффициентов модели, тогда получим такое:
\[ \sum_{i=1}^n (y_i - \hat y_i) + \lambda \sum_{j=1}^p |b_j| \rightarrow \underset{b}{\min} \] Такой подход называется LASSO-регрессия.
Существует и промежуточный вариант:
\[ \sum_{i=1}^n (y_i - \hat y_i) + \lambda_1 \sum_{j=1}^p |b_j| + \lambda_2 \sum_{j=1}^p b_j^2 \rightarrow \underset{b}{\min} \]
Он называется метод эластичной сети.
Во всех выражениях выше \(\lambda\) — это штрафной коэффициент, который и определяет величину штрафа.
23.1.1 Пример работы штрафного коэффициента
Чтобы наглядно увидеть, как работает регуляризация и на что влияет штрафной коэффициент, подберем коэффициенты для самой простой линейной модели на «игрушечных» данных. Подбор проведём двумя методами — обычным МНК и ridge-регрессией.
Пусть у нас есть такие данные:
| \(y_i\) | \(x_i\) |
|---|---|
| 10 | 1 |
| 20 | 1 |
| 30 | 2 |
Модель возьмём самую простую — \(y_i = \beta x_i + \varepsilon_i\). Даже без интерсепта. Подберём оценку коэффициента \(\hat \beta = b\) методом наименьших квадратов.
Напомним, что в МНК мы минимизируем RSS, которая в даном случае будет выражаться так:
\[ RSS = \sum_{i=1}^n (y_i - \hat y_i)^2 = \sum_{i=1}^n (y_i - bx_i)^2 = \\ = \sum_{i=1}^n (y_i^2 - 2 y_i bx_i + b^2 x_i^2) = \\ = \sum_{i=1}^n y_i^2 - 2b \sum_{i=1}^n x_i y_i + b^2 \sum_{i=1}^n x_i^2 = Q(b) \]
Мы получили выражение для RSS, от которого теперь можем взять производную, чтобы затем приравнять её к нулю и найти мнимум функции:
\[ Q'(b) = -2 \sum_{i=1}^n x_i y_i + 2 b \sum_{i=1}^n x_i^2 = 0 \]
\[ b = \frac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i^2} \\ b = \frac{10 + 20 + 60}{1 + 1 + 4} = \frac{90}{6} = 15 = \hat \beta_{\text{МНК}} \]
Итак, мы получили оценку коэффициента методом наименьших квадратов. Теперь посмотрим, что изменится, если мы будем использовать подход регуляризованной регрессии.
В ridge-регрессии, которую мы возьмём для примера, минимизируется RSS плюс сумма квадратов коэффициентов модели. В нашем случае:
\[ RSS + \lambda b^2 \rightarrow \underset{b}{\min} \]
Функция \(Q_R(b)\) очень похожа на функцию \(Q(b)\) и отличается от неё наличием дополнительного слагаемого \(\lambda b^2\), которое и выражает штраф:
\[ Q_R(b) = \sum_{i=1}^n y_i^2 - 2b \sum_{i=1}^n x_i y_i + b^2 \sum_{i=1}^n x_i^2 + \lambda b^2 \]
Производная будет выглядеть так:
\[ Q'_R(b) = -2 \sum_{i=1}^n x_i y_i + 2 b \sum_{i=1}^n x_i^2 + 2 b \lambda = 0 \]
Пока всё логично. Магия начинается сейчас.
\[ b = \frac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i + \lambda} \]
Штрафной коэффициент \(\lambda\) оказывается в знаменателе, а значит он будет оказывать прямое влияения на величину коэффициента. Скажем, если мы возьмем его значение \(\lambda = 240\), то получим следующее:
\[ b = \frac{90}{6 + 240} < 1 \]
Таким образом, значение коэффициента было «оштрафовано» и в результате мы подучили значительно меньшее его значение. Конечно, этот пример игрушечный, но с механизмом регуляризации вы теперь знакомы.
23.2 Регуляризованная регрессия в R
23.2.1 Данные
Сегодня мы работаем с данными про менеджеров-продажников. Данные содержат информацию о некоторых характеристиках менеджеров (количественные шкалы Fx, Cs, Sy, Sp, In, Em, Re, Sc, Ie, Do), а также сумму, на которую менеджер напродавал. Наша задача узнать, какие характеристики менеджеров сильнее всего связаны с их эффективностью в продажах.
Подключаем пакеты, которые нам понадобятся:
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──## ✓ ggplot2 3.3.2 ✓ purrr 0.3.4
## ✓ tibble 3.0.4 ✓ dplyr 1.0.2
## ✓ tidyr 1.1.2 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.0## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()## Loading required package: Matrix##
## Attaching package: 'Matrix'## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpack## Loaded glmnet 4.0-2Грузим данные:
## tibble [281 × 12] (S3: tbl_df/tbl/data.frame)
## $ Fx : num [1:281] 12 14 17 18 20 21 23 26 26 26 ...
## $ Cs : num [1:281] 75 21 37 81 85 28 14 4 45 48 ...
## $ Sy : num [1:281] 52 38 39 12 51 55 57 56 69 44 ...
## $ Sp : num [1:281] 21 24 22 25 29 23 33 16 25 30 ...
## $ In : num [1:281] 32 66 56 45 74 104 55 36 38 41 ...
## $ Em : num [1:281] 55 59 54 55 36 44 20 21 15 27 ...
## $ Re : num [1:281] 18 54 44 61 53 61 50 52 57 31 ...
## $ Sc : num [1:281] 57 29 71 44 56 36 34 55 25 41 ...
## $ Ie : num [1:281] 66 75 41 18 57 71 79 67 43 23 ...
## $ Do : num [1:281] 54 41 32 51 35 41 23 8 46 38 ...
## $ group : num [1:281] 0 0 0 0 0 0 0 0 0 0 ...
## $ prodazhi: num [1:281] 245330 197980 228990 294930 245670 ...Немного подредактируем данные, чтобы проще записывать модели — уберем колонку group, которая нам не понадобится в анализе:
23.2.2 Особенности синтаксиса пакета glmnet
Функция, позволяющая строить модель регуляризованной регрессии, находится в пакете glmnet и называется cv.glmnet(). При подборе коэффициентов модели она проводит кросс-валидацию, что позволяет получить ещё более точные оценки параметров.
У функции несколько непривычный синтаксис: она требует на вход отдельно вектор целевой переменной и отдельно матрицу предикторов. Придется немного подготовить даннные.
Выносим целевую переменную в отдельный вектор:
Создаем матрицу предикторов:
Теперь всё готово к тому, чтобы строить модели.
23.2.3 Ridge-регрессия в R
Чтобы подобрать коэффициенты модели с помощью ridge-регрессии, надо указать в функции cv.glmnet() аргумент alpha = 0:
Модель зафитилась. Можно посмотреть интересный график с помощью функции plot().
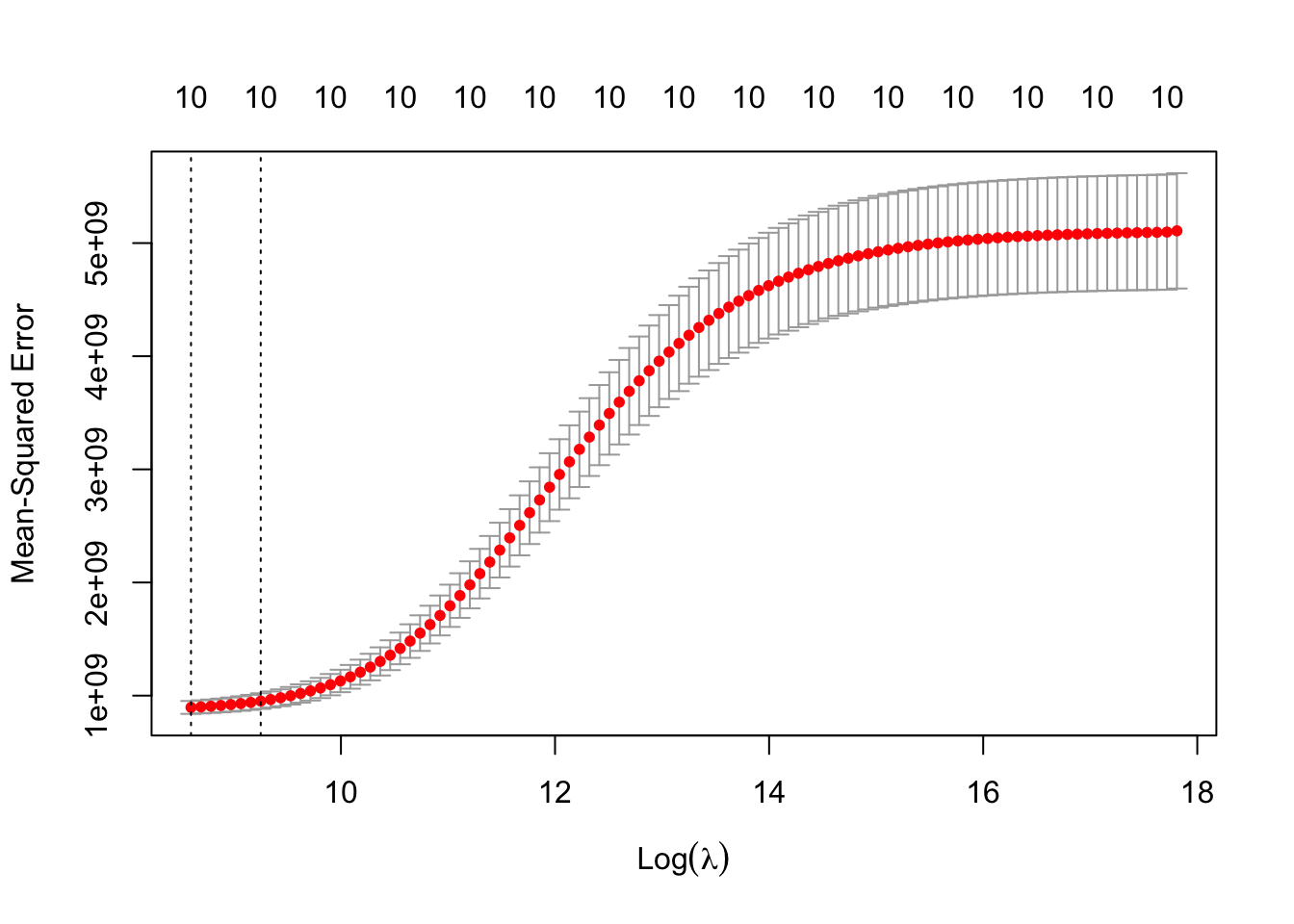
На этом графике по оси \(x\) оторажается логарифм1 штрафного коэффициента \(\lambda\), по оси \(y\) — средняя квадратичная ошибка модели (MSE). Можно пронаблюдать, как в среднем меняется ошибка модели с увеличением штрафного коэффициента (красные точки). Серые «усы» показывают границы — минимум и максимум — ошибки на разных подвыборках кросс-валидации.
Первая вертикальная линия — это значение штрафного коэффициента \(\lambda_\min\), при котором значение MSE минимально. Обычно для анализа берут именно это значение. Но есть ещё одно — вторая вертикальная линия —- значение штрафного коэффициента \(\lambda_{1\text{SE}}\), которое находится на расстоянии одной стандартной ошибки от минимального. Иногда в такой модели получаются более интересные результаты.
Числа над графиком обозначают количество предикторов, которое осталось в модели при данном значении штрафного коэффициента. Мы видим, что там всегда 10, а мы ввели в модель как раз 10 предикторов. Это справедливо, так как ridge-регрессия склонна оставлять все предикторы в модели, поэтому если ваша приоритетная задача — получить точные оценки для всех коэффициентов, используйте этот тип регуляризации.
Вывести полученные коэффициенты можно с помощью функции coef():
## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 71576.733397
## Fx -29.371027
## Cs 301.410249
## Sy 55.689983
## Sp 2803.154449
## In -9.111458
## Em 10.242251
## Re 125.829420
## Sc -19.378065
## Ie 281.959450
## Do 1577.944735## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 84137.604175
## Fx 7.372755
## Cs 405.747686
## Sy 66.757097
## Sp 2624.327321
## In -11.827377
## Em -9.814379
## Re 123.189929
## Sc -20.132521
## Ie 272.879794
## Do 1378.815378Здесь нам доступны только сами оценки коэффициентов. К сожалению, после того, как мы вводим штраф в алгоритм подбора модели, мы теряем возможность тестировать статистические гипотезы. Поэтому мы не можем сказать, значимо ли влияние In с коэффициентом \(-9\) или нет.
Но всё-таки можно кое-что сделать…
23.2.4 LASSO-регрессия в R
Для LASSO-регрессии всё остаётся точно так же, за исключением того, что необходимо указать alpha = 1:
Посмотрим график:
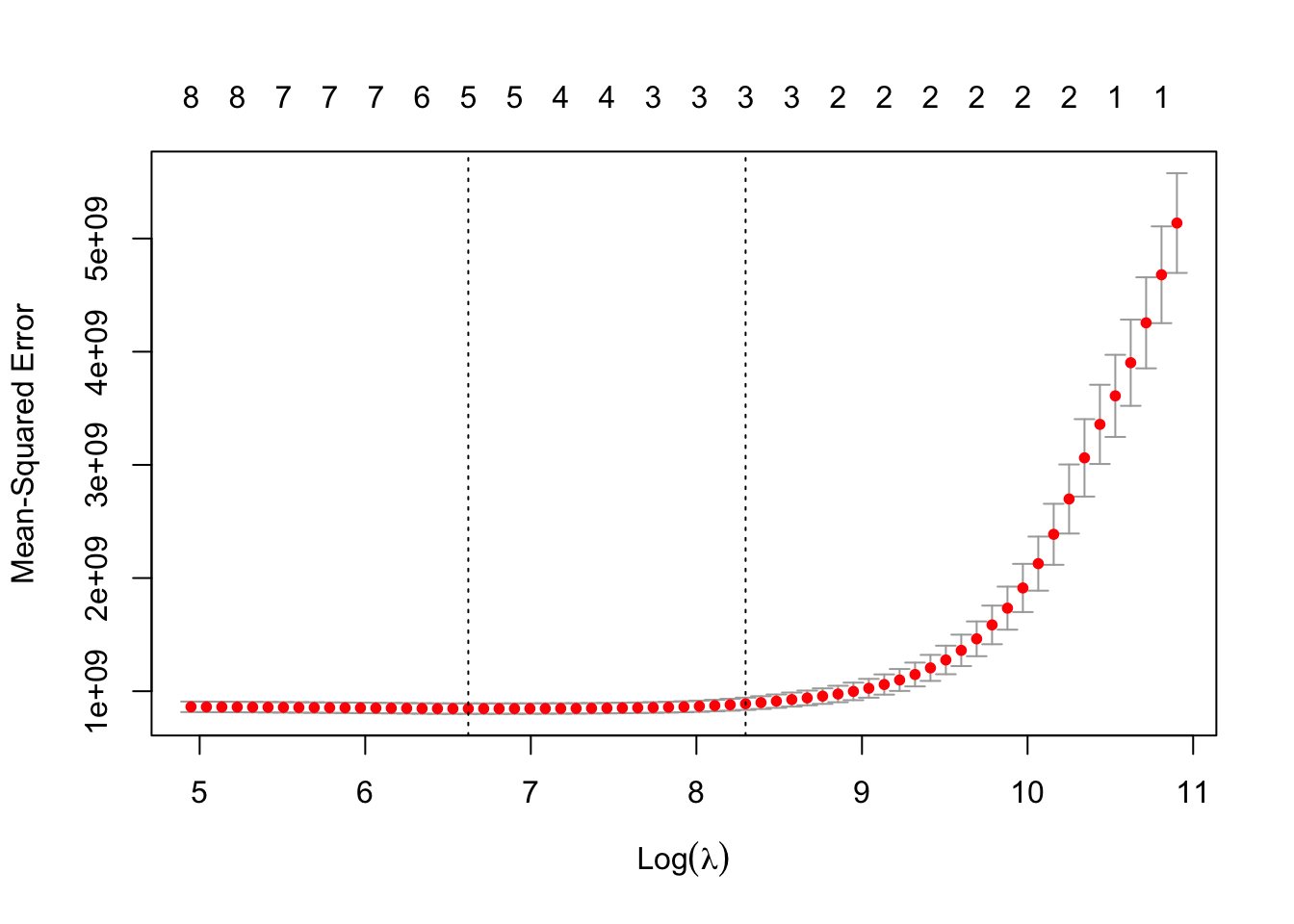
Ход движения линии изменился, что, в целом, ожидаемо, ведь мы использовали другой тип регуляризации. Значения всех элементов графика здесь абсолютно то же самое, что и в предыдущем случае. Интересно другое.
Теперь на графиков числа умпеньшаются по мере увеличения [логарифма] штрафного коэффициента. Это происходит потому, что LASSO-регрессия склонна занулять предикторы, поэтому если ваша приоритетная задача — отбор предикторов, то ваш выбор — именно этот тип регуляризации.
Посмотрим, что теперь покажет функция coef():
## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 64600.42023
## Fx -26.67118
## Cs .
## Sy .
## Sp 2961.59762
## In .
## Em .
## Re 77.02326
## Sc .
## Ie 245.53010
## Do 1965.85258## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 93218.80011
## Fx .
## Cs .
## Sy .
## Sp 2772.36804
## In .
## Em .
## Re .
## Sc .
## Ie 88.24356
## Do 1774.30021У ряда предикторов нет коэффициента, что говорит нам о том, что он был обнулён. Это можно рассматривать как аналог тестирования статистической значимости, конечно с большими оговорками. Но идейно: если коэффициент не обнулился, то он статистически значим, если однулился — то не значим. Заметьте, что в зависимости от того, какой штрафной коэффициент мы выберем, у нас будет зануляться различное число коэффциентов.
Регуляризованная регрессия часто используется в индустрии, так как этот подход не усложняет саму модель и не вносит сложности в интерпретацию предикторов, однако вместе с тем помогает бороться со множеством проблем индустриальных данных, в частности, мультиколлинеарностью.
Так просто удобнее визуализировать.↩︎