9 Математический ликбез

9.1 Элементы алгебры логики

Логика исследует закономерности мышления, но делает это отлично от того, как этим занимается, например, психология. Формальная логика абстрагируется от связей мышления с какими-либо сторонами сознания и сосредотачивается на логической непротиворечивости и последовательности мышления. Таким образом, формальная логика — это наука об общих структурах правильного мышления в его языковой форме.

Логика — это нормативная наука, то есть она определяет, как оно должно быть, в то время как, например, психология исследуется как оно есть и как и почему логические законы нарушаются.

9.1.1 Высказывания

Логика как наука имеет дело, прежде всего, с высказываваниями. Высказывание отражает определённую объективную¹ связь между предметами. Высказывание истинно, если в нём содержится адеквантное отражение этой связи — в ином случае высказывание ложно. В общем случае высказывание существует с форме повествовательного предложения.

Например, высказывание «Земля вращается вокруг Солнца» отражает объективное отношение, поэтому оно истинно, а высказывание «страницы этой книги зелёного цвета» не адекватно отражает существующее положение дел, поэтому оно ложно.

Прежде всего, нас будут интересовать атомарные высказывания. Это элементарные высказывания, которые невозможно разделить на составляющие — более мелкие высказывания. Например, «четыре — это целое число» — это атомарное высказывание.

Мы уже сталкивались с логическими операциями в R (например, при сабсете данных). Подумайте, какие атомарные высказывания могли бы быть сформулированы в той области, которую мы изучаем.

Атомарные высказывания могут быть либо истинны, либо ложны. Почему? Потому что мы находимся в рамках двузначной логики². Атомарные высказывания могут быть обозначены пропозициональными переменными. Так же как и числа в математике могут быть заменены буквеными обозначениями для абстрагирования от значения числа, так же и высказывания заменяются переменными для абстрагирования от содержания высказывания. Для обозначения пропозициональных переменных используются латинские буквы. А так как само высказывания имеет опредлённое значение истинности (истина, или TRUE, и ложь, или FALSE), то и переменная, которой мы обозначаем это высказывание, также будет обладать этим же значением истинности. Всё аналогично математике.

9.1.2 Логические операции

С атомарными высказываниями можно выполнять различные логические операции.

9.1.2.1 Инверсия

Самая простая операция — инверсия, или отрицание. Оно обозначается с помощью оператора $\neg$. Это унарная операция, то есть она применяется к одной переменной. При отрицании значение истинности высказывания изменяется на противоположное, поэтому мы можнм составить следующую таблицу истинности для отрицания:

$p$	$\neg p$
`TRUE`	`FALSE`
`FALSE`	`TRUE`

В данном случае с помощью переменной $p$ обозначено некоторые атомарное высказывание.

Особо стоит отметить, что при отрицании отрицается всё высказывание целиком, а не какой-то отдельный его элемент. То есть формально правильным вариантом отрицания высказывания «все лебеди белые» будет следующий — «неверно, что все лебеди белые».

Графически инверсия отображается так:

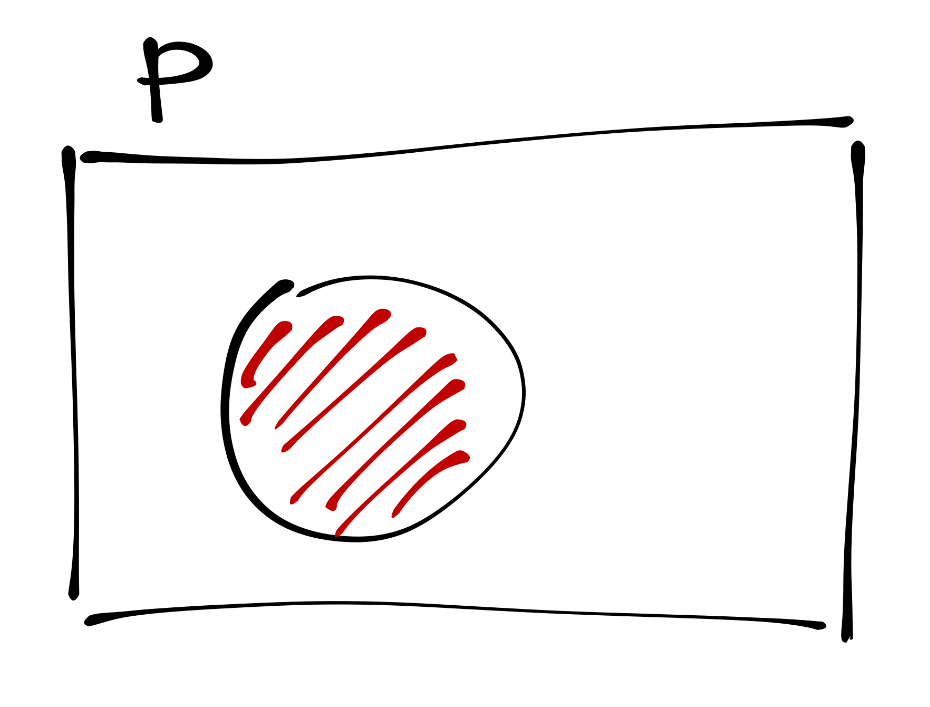
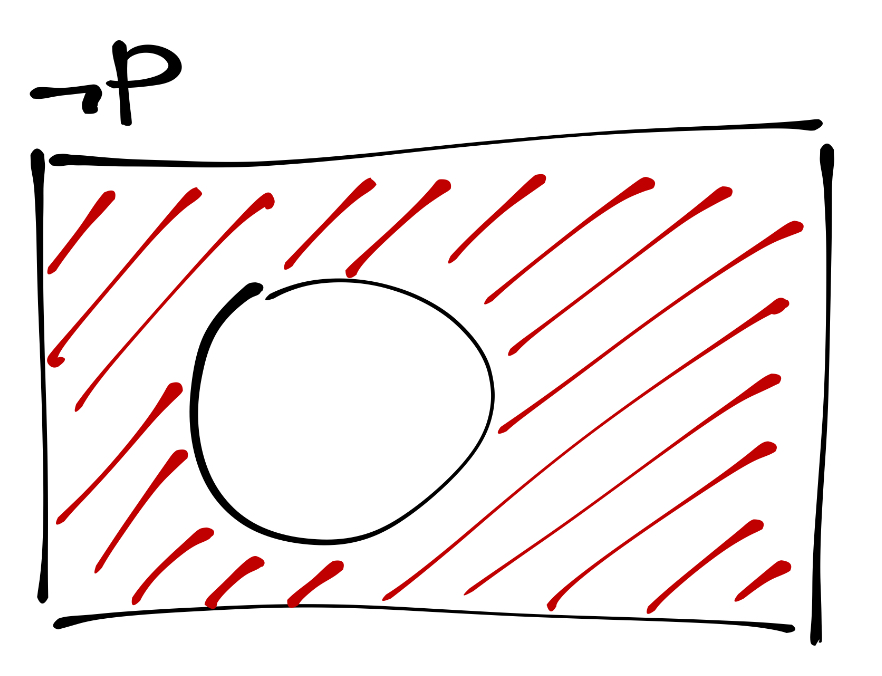
Кружком обозначена часть пространства, где утверждение истинно. Соответственно, в любой иной области пространства оно ложно.

9.1.2.1.1 Инверсия в R

Оператор отрицания в R обозначается восклицательным знаком !. Если его поставить перед некоторой командой, которая возвращает логическое значение, то этот оператор изменит его на противоположное:

3 > 6; !(3 > 6)

## [1] FALSE

## [1] TRUE

"sing" == "sign"; !("sing" == "sign"); "sing" != "sign"

## [1] FALSE

## [1] TRUE

## [1] TRUE

a <- c(TRUE, FALSE, FALSE, TRUE); !a

## [1] FALSE  TRUE  TRUE FALSE

9.1.3 Сложные высказвания

Из атомарных высказываний можно составлять сложные высказывания при помощи логических операторов. Например, высказывание «если четыре делится на два, то четыре — чётное число» является сложным, посколько состоит из двух атомарных — «четыре делится на два» и «четыре — чётное число» — соединённых союзом «если…, то…».

Далее мы пристумаем с знакомству с бинарными операторами, то есть такими, которые функционируют на двух аргументах.

9.1.3.1 Конъюнкция

Конъюнкция (логическое умножение, логические И) представляет собой такое высказывание, которое наиболее точно передается следующей конструкцией естественного языка — «как $p$, так и $q$». $p$ и $q$ в данном случае пропозициональные переменные, которые заменяют конкретные высказывания. Конъюнкция истинна тогда и только тогда, когда обе пропозициональные переменные, входящие в её состав, имеют значении истинности TRUE. В любом ином случае конъюнкция ложна.

Конъюнкция обозначается символом $\wedge$ и имеет следующую таблицу истинности:

$p$	$q$	$p \wedge q$
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`FALSE`
`FALSE`	`TRUE`	`FALSE`
`FALSE`	`FALSE`	`FALSE`

Графически конъюнкция отображается так:

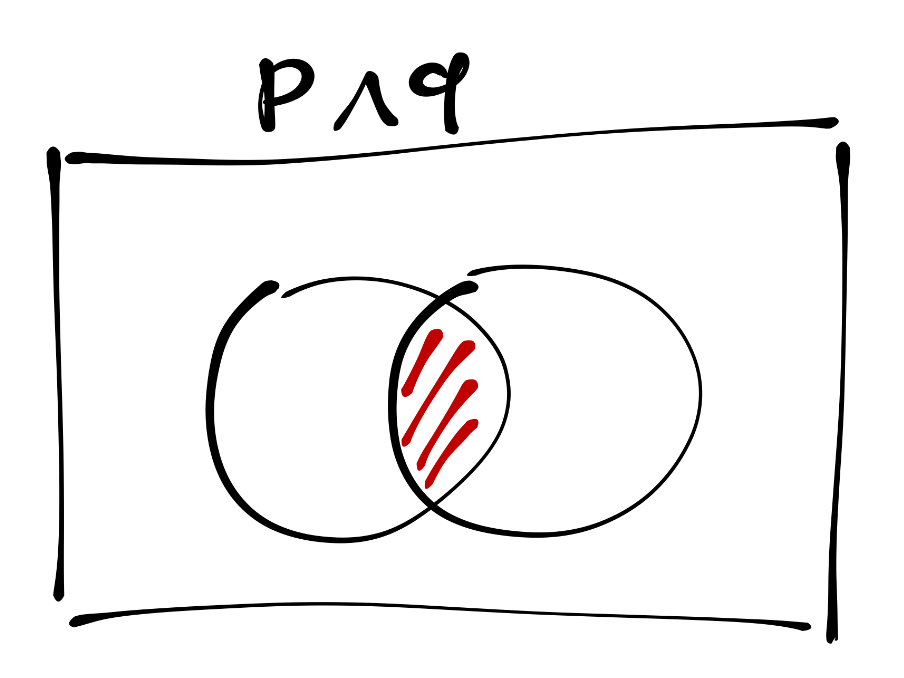
9.1.3.1.1 Конъюнкция в R

В качестве оператора логического И в R используется символ &:

4 != 2 & 1 > 4

## [1] FALSE

4 != 2 & 1 < 4

## [1] TRUE

a <- c(TRUE, TRUE, FALSE, FALSE); b <- c(TRUE, FALSE, TRUE, FALSE)
a & b

## [1]  TRUE FALSE FALSE FALSE

9.1.3.2 Дизъюнкция

Дизъюнкция (логическое сложение, логические ИЛИ) представляет собой такое высказывание, которое наиболее точно передается следующей конструкцией естественного языка — «или $p$, или $q$, или и то и другое». Поэтому дизъюнкция истинна тогда, когда хотя бы одна пропозициональная переменная, входящая в её состав, имеет значении истинности TRUE. В случае, если оба высказывания ложны, дизъюнкция будет ложна.

Дизъюнкция обозначается символом $\vee$ и имеет следующую таблицу истинности:

$p$	$q$	$p \vee q$
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`TRUE`
`FALSE`	`TRUE`	`TRUE`
`FALSE`	`FALSE`	`FALSE`

Графически дизъюнкция отображается так:

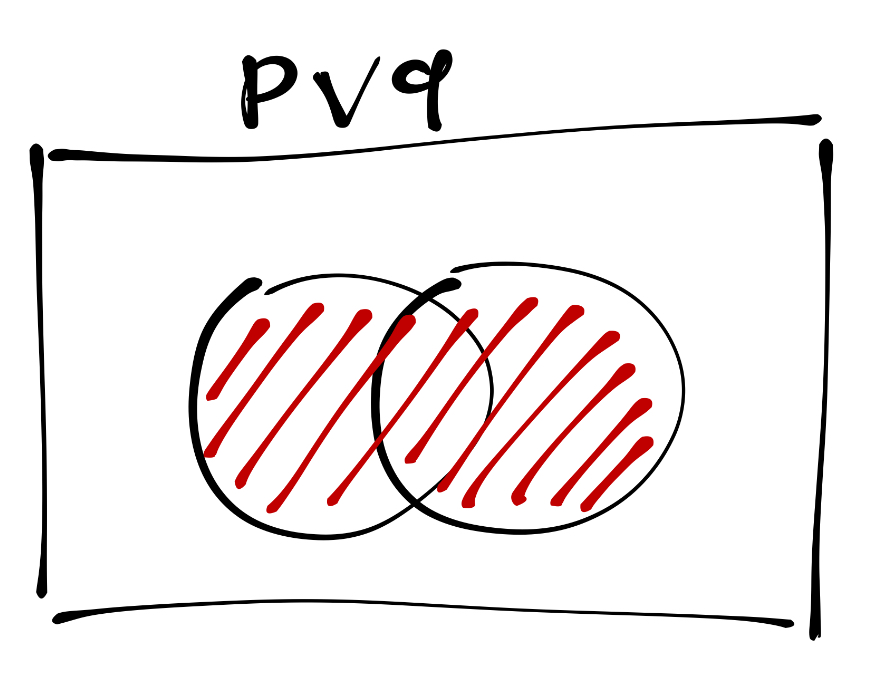
9.1.3.2.1 Дизъюнкция в R

В качестве оператора логического ИЛИ в R используется символ |:

4 != 2 | 1 > 4

## [1] TRUE

4 == 2 | 1 == 4

## [1] FALSE

a <- c(TRUE, TRUE, FALSE, FALSE); b <- c(TRUE, FALSE, TRUE, FALSE)
a | b

## [1]  TRUE  TRUE  TRUE FALSE

9.1.3.3 Разделительная дизъюнкция

Разделительная дизъюнкция (исключающее ИЛИ) — это такое высказывание, которое наиболее полно описывается следующим выражением естественного языка — «либо $p$, либо $q$». На её графическом представлении хорошо видно, чем она отличается от обычной дизъюнкции — она исключает ту часть пространства, где верны оба высказывания:

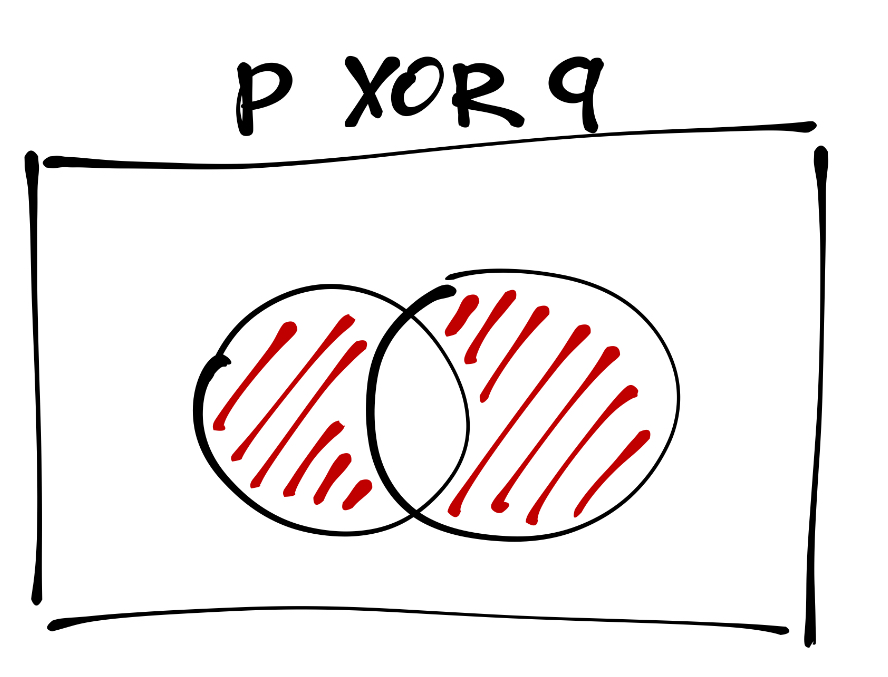
Для обозначения разделительно дизъюнкции есть много различных операторов, но мы будем записывать её так — $p \; \mathrm{XOR}\; q$. По иллюстрации можно восстановить таблицу истинности для этого оператора:

$p$	$q$	$p \; \mathrm{XOR}\; q$
`TRUE`	`TRUE`	`FALSE`
`TRUE`	`FALSE`	`TRUE`
`FALSE`	`TRUE`	`TRUE`
`FALSE`	`FALSE`	`FALSE`

Таким образом, видно, что исключающее ИЛИ истинно тогда, когда значения истинности пропозициональных переменных, входящих в сложное высказывание, различны.

9.1.3.3.1 Разделительная дизъюнкция в R

В R эта логическая функция реализована, в отличие от предыдущих, не как оператор, а как функция с соответствующим названием:

a <- c(TRUE, TRUE, FALSE, FALSE); b <- c(TRUE, FALSE, TRUE, FALSE)
xor(a, b)

## [1] FALSE  TRUE  TRUE FALSE

9.1.4 Условные высказывания

9.1.4.1 Импликация

Сложное высказывание, описываемое конструкцией естественного языка «если $p$, то $q$» в формальной логике носит название импликации. Она отражает следование одного утверждения из другого и обозначается следующим образом — $p \rightarrow q$. Высказывание $p$ называется антецедентом имликации, а $q$ — консеквентом.

Импликация имеет следующую таблицу истиности:

$p$	$q$	$p \rightarrow q$
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`FALSE`
`FALSE`	`TRUE`	`TRUE`
`FALSE`	`FALSE`	`TRUE`

Как видно из таблицы, импликация ложна только тогда, когда её антецедент истинен, и консеквент — ложен. Но что более интересно, так это то, что, согласно таблице, из ложного утверждения может следовать любое³. Это факт мы вспомним, когда будем обсуждать тестирование статистических гипотез.

Импликацию утвержает то же самое, что и следующее сложное высказывание — $\neg (p \wedge \neg q)$. Отсюда можно получить графическое изображение импликации:

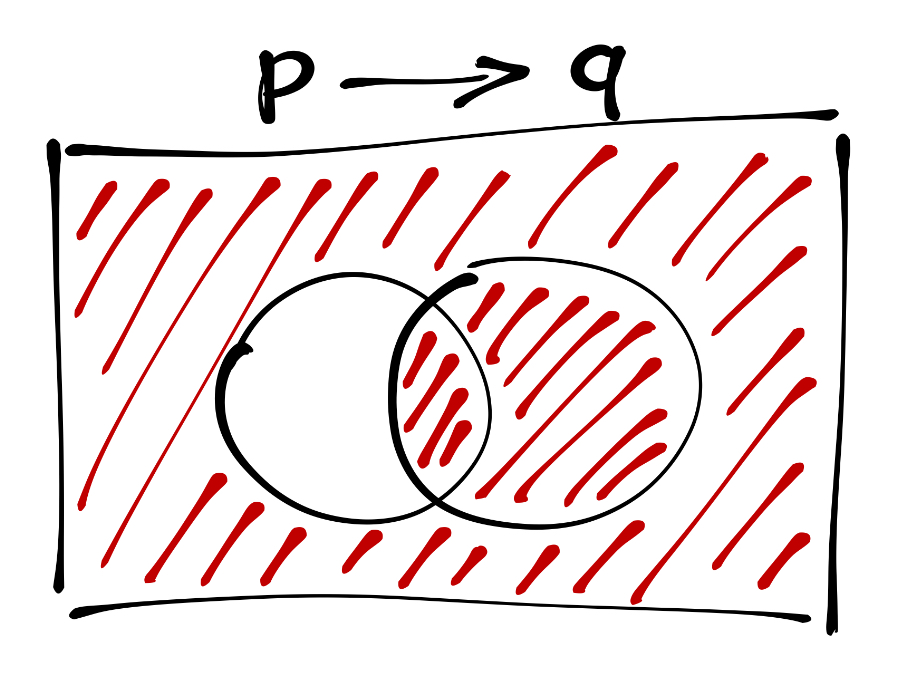
Таблица истинности для импликации $p \rightarrow q$ у нас есть. Постройте таблицу истинности для высказывания $\neg (p \wedge \neg q)$ и проверьте, действительно ли значенния истинности обоих сложных высказывания совпадают.

9.1.4.2 Репликация

Репликация похожа на импликацию, но действует как бы в обратном направлении, что отражено в её обозначении — $p \leftarrow q$. Эта конструкция читается как «$p$ реплицирует $q$» и является эквивалентом естественноязыкового «только если $p$, то $q$». Соответствующим образом изменяется и таблица истиности:

$p$	$q$	$p \leftarrow q$
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`TRUE`
`FALSE`	`TRUE`	`FALSE`
`FALSE`	`FALSE`	`TRUE`

Идея здесь в том, что если мы получили в результате ложь, то истины в начале быть не могло. Графическое изобажение репликации выглядит так:

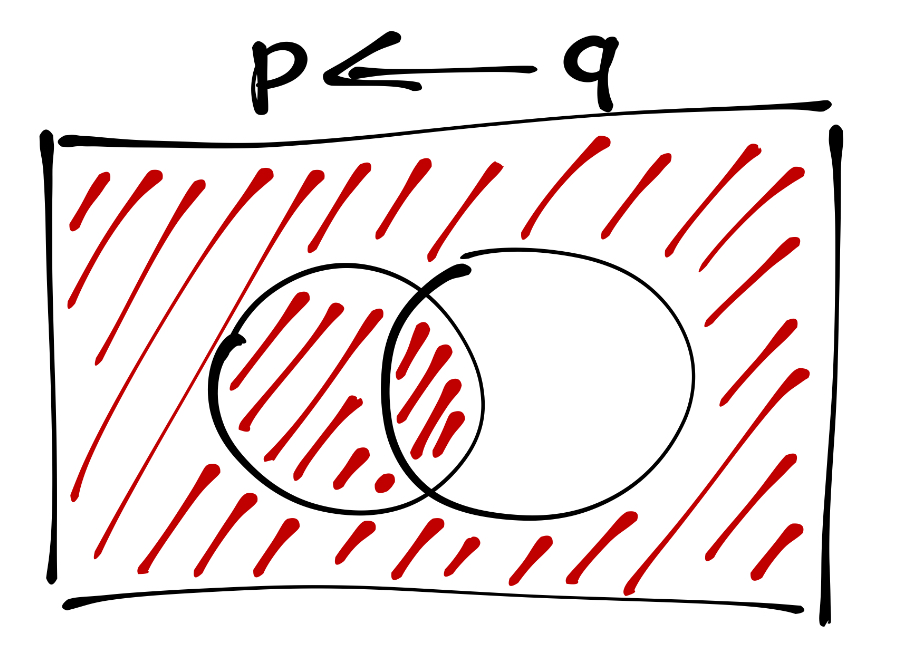
Выведите равносильное репликации высказывание, содержащее только операторы инверсии, конъюнкции и дизъюнкции. Под равносильностью мы пониманием одинаковый набор значений истинности двух утверждений.

Для импликации $p \rightarrow q$ таким утверждением является $\neg (p \wedge \neg q)$. А для репликации?

9.1.4.3 Эквиваленция

Если мы соединим с помощью конъюнкции импликацию и репликацию, то есть запишем вот такое высказывание — $(p \rightarrow q) \wedge (p \leftarrow q)$ — то получим эквиваленцию. По своей сути она является логическим отражением языковой конструкции «только если $p$, то $q$», поэтому она обозначается вот так — $p \leftrightarrow q$ — и её таблица истинности выглядит соответствующим образом:

$p$	$q$	$p \leftrightarrow q$
`TRUE`	`TRUE`	`TRUE`
`TRUE`	`FALSE`	`FALSE`
`FALSE`	`TRUE`	`FALSE`
`FALSE`	`FALSE`	`TRUE`

Из неё легко вывести графическое представление эквиваленции:

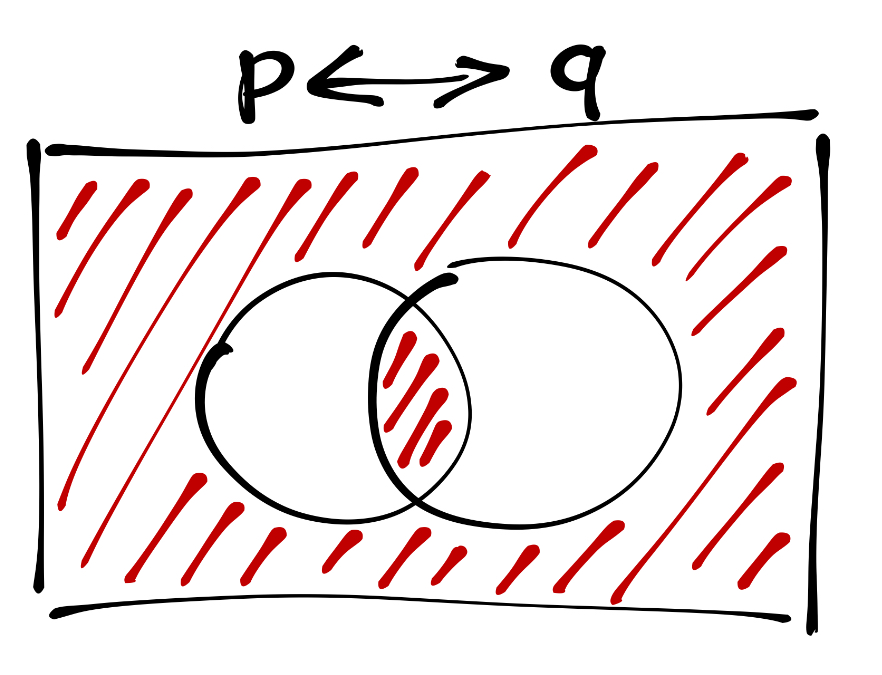
Проверьте, действительно ли равносильны высказывания $p \leftrightarrow q$ и $(p \rightarrow q) \wedge (p \leftarrow q)$. Для этого необходио построить таблицу истинности для представленно конъюнкции.

9.2 Элементы теории множеств

На базе теории множеств стоит вся современная математика. Мы ознакомимся только в некоторыми концепциями этого раздела математики, но вообще полезно с ним познакомиться гораздо глубже.

9.2.1 Множество

Понятие множества неопределимо. По крайней мере силами самой теории множеств. Но мы будем понимать под множеством совокупность, или набор, некоторых (любых) объектов. Это могут быть числа, буквы, точки и любые другие объекты. Объекты, входящие в состав мноежства, называются элементами этого множества.

Множества обозначают заглавными латинскими буквами (например, $A$), а его элемента прописными латинскими буквами (например, $a_1$, $a_2$ и т.д.).

Множества удобно изображать кружочками. Примерно так:

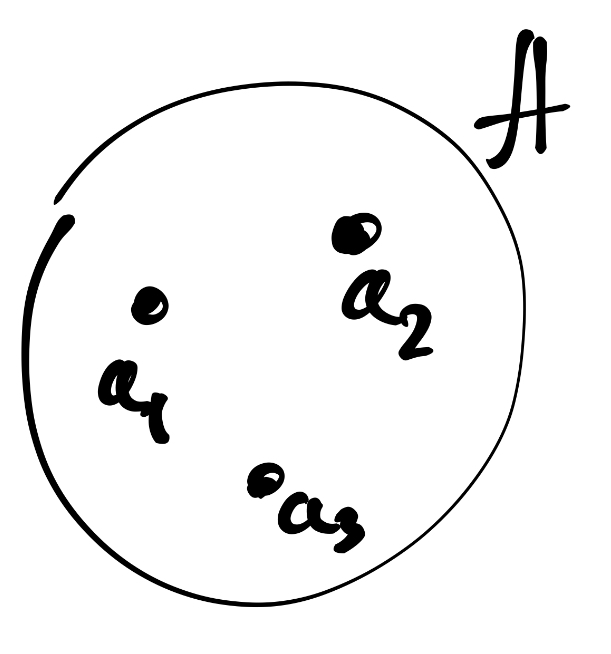
Если элемент входит в данное множество, то мы говорим, что этот элемент принадлежит данному множеству, и записываем это следующим образом:

\[ a_i \in A \]

Символ $\in$ читается как «принадлежит».

Если мы хотим задать множество через перечисление элементов, то можно это сделать так:

\[ B = \{0, 1, 2, 3, 4, 5\} \] В данном случае множество $B$ содержит 6 элементов — числа от нуля до пяти.

Приведём примеры множеств.

Множество букв русского алфавита:

\[L = \{\text{а, б, в, г, д, …, э, ю, я}\}\]

Множество всех натуральных чисел⁴:

\[\mathbb{N} = \{0, 1, 2, 3, \dots\}\]

Множество всех целых чисел:

\[\mathbb{Z} = \{0, 1, -1, 2, -2, 3, -3, \dots\}\]

Также из числовых множеств мы можем вспомнить рациональные числа $\mathbb{Q}$, действительные (вещественные) числа $\mathbb{R}$ и комплексные числа $\mathbb{C}$.

Мы можем взять и рассмотреть не все элементы какого-то множества, а какую-то их часть. Например, взять элементы $a_1$ и $a_2$ и объединить их в множество поменьше.

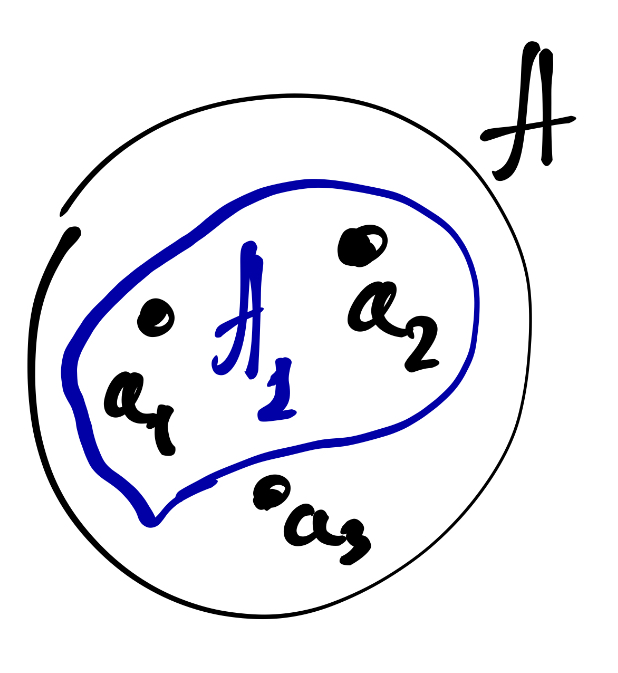
Мы получим множество $A_1 = \{a_1, a_2\}$, которое является подмножеством множества $A$. Иначе говоря, множества $A_1$ включается во множество $A$:

\[ A_1 \subset A \]

В частности, множество натуральных чисел включается во множество целых — $\mathbb{N} \subset \mathbb{Z}$. А если продолжить эту цепочку, то можно получить что-то такое:

\[ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} \]

Вот такая пирамижка получается.

9.2.2 Операции над множествами

Над множествами можно производить определённые операции. Во-первых, множества можно складывать, или объединять:

\[ A + B = A \cup B = \{x: x \in A \vee x \in B\} \]

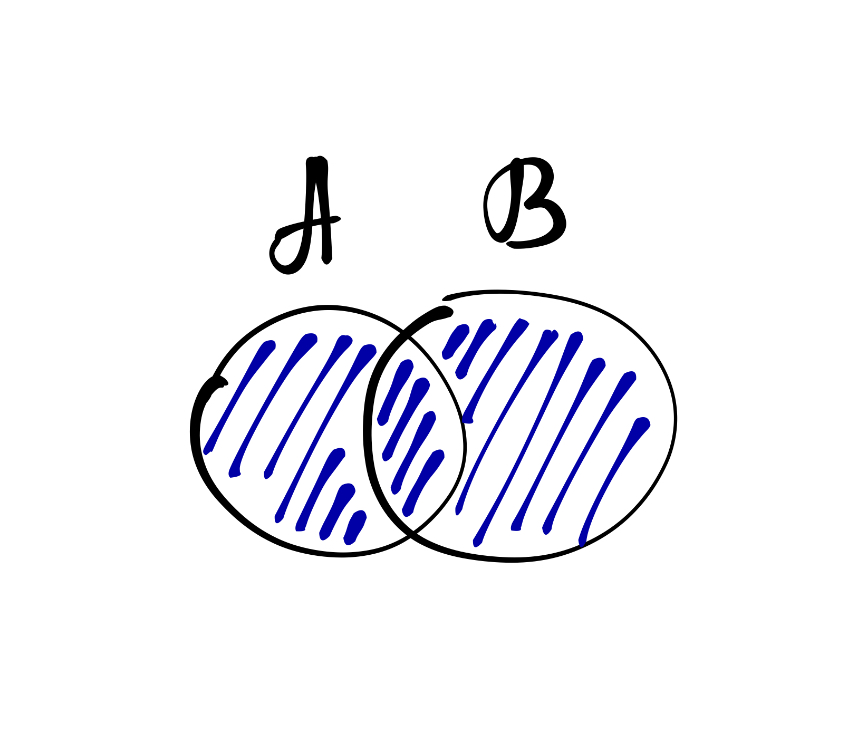
Тогда в новом множестве окажутся все элементы обоих исходных множеств. Что-то это напоминает.

Во-вторых, множества можно умножать, или находить их пересечение:

\[ A \cdot B = A \cap B = \{x: x \in A \wedge x \in B\} \]

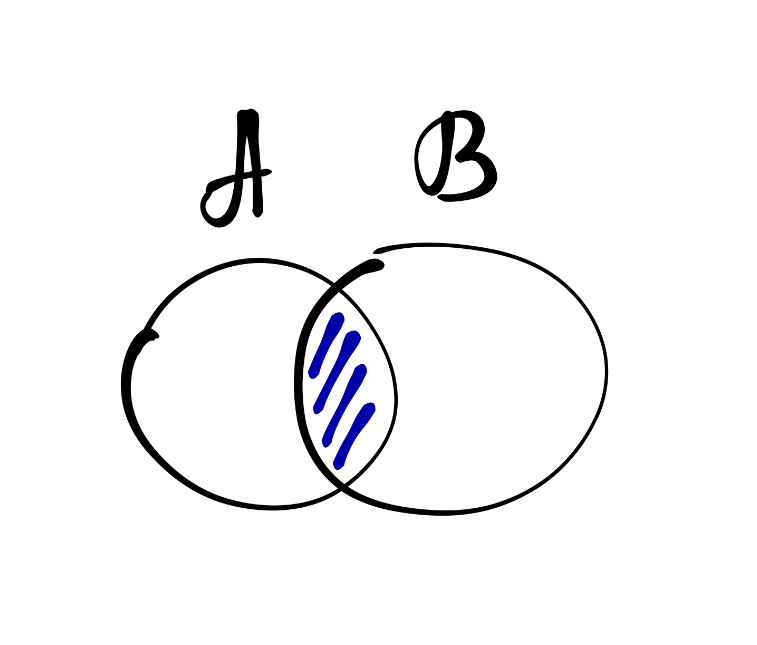
Тогда в новом множестве окажутся те элементы, которые принадлежат обоим множествам сразу. Это тоже что-то напоминает.

В-третьих, можно искать разность множеств — такая операция называется дополнение:

\[ A \backslash B = \{x: x \in A \wedge x \notin B\} \]

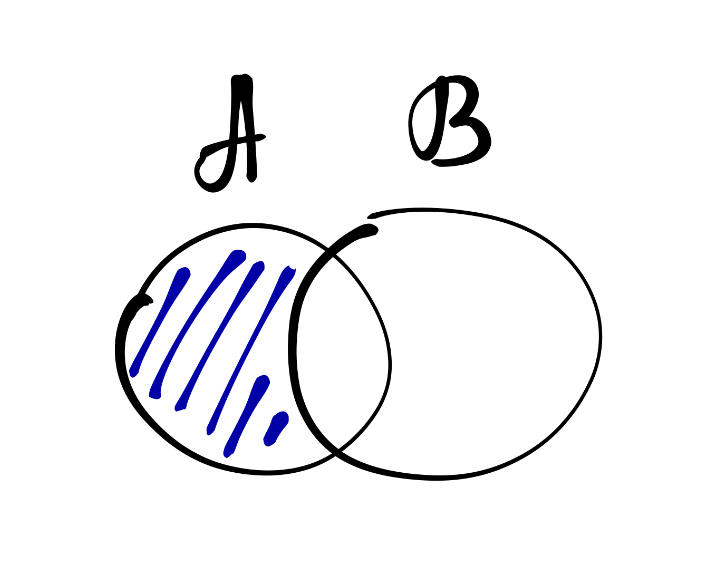
А ещё можно вычитать множества друг из друга, то есть искать их симметрическую разность:

\[ A \, \triangle \, B = (A \backslash B) \cup (B \backslash A) = \{x: x \in A \, \mathrm{XOR}\, x \in B\} \]

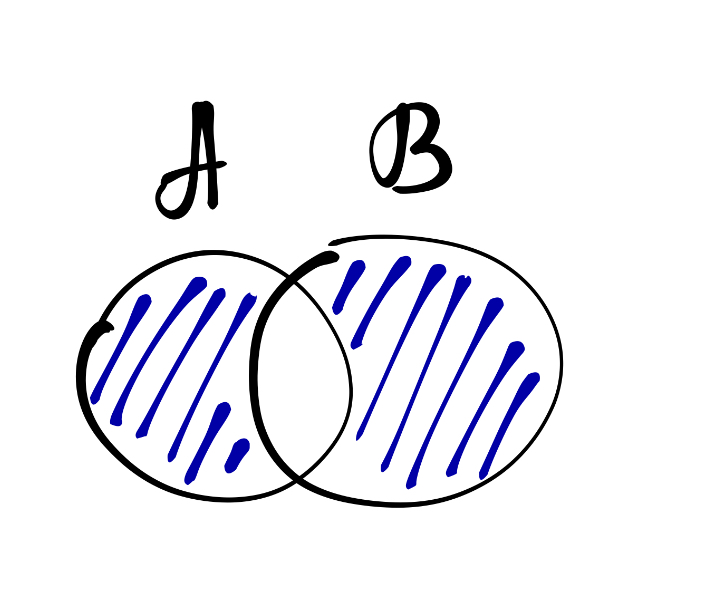
У меня снова déjà vu.

Ну, и самый смак — декартово произведение двух множеств. Пусть у нас есть два множества $A$ и $B$. Тогда их декартово произведение представляет собой множество всех возможных упорядоченных пар $(a, b), a \in A, b \in B$.

\[ A \times B = \{(a, b): a \in A, b \in B\} \]

Упорядоченность подразумевает, что если мы будем перемножать $A \times B$, то будут получаться пары $(a,b)$, а если $B \times A$, то пары $(b, a)$.

Пример интересного декартова произведения множеств представлен на картинке. Это произведение множества $\{в, и, к\}$ на множество цветов радуги:

9.2.3 Отображения

Мы можем сопоставлять элементы много множества элементам другого. Тогда мы получим отображение. Например, мы можем взять множество букв латинского алфавита и сопоставить каждому элменту этого множества число, которое будет отображать позицию буквы в алфавите. Пусть у нас есть множество $L = \{\text{a, b, c, d,…, x, y, z}\}$ и множество $N = \{1, 2, 3, \dots, 24, 25, 26\}$. Тогда мы можем задать такое отображение:

\[ F: L \rightarrow N \]

Более того, мы даже можем реализовать его в R:

letter_number <- function(x) {
  which(x == letters)
}
letter_number("a"); letter_number("z"); letter_number("i")

## [1] 1

## [1] 26

## [1] 9

Заметьте, что мы реализовали в коде отображение, написав функцию. Это не случайно. Не вдаваясь в детали, можно сказать, что термины «отображение» и «функция» — синонимы. Ведь по сути что делает [математическая] функция? Сопоставляет между собой значения числовых множеств. То есть отображает одно множество в другое.

Например, простая функция $y = x$⁵ отображает множество вещественных чисел в само себя: $F: \mathbb{R} \rightarrow \mathbb{R}$. Функция модуля $y = |x|$ отображает множество вещественных чисел во множество положительных вещественных чисел: $F: \mathbb{R} \rightarrow \mathbb{R_+}$. И так далее.

Вот такая вот интересная история.

9.3 Немного комбинаторики

9.3.1 Перестановки

Представим такую задачу: нам необходимо расставить книги на полке. Всего у нас есть пять книг. Сколькими способами мы это сможем сделать?

Подойдём к вопросу технически: возьмем и начнём расставлять. На первое место мы можем поставить любую из пяти книг, то есть вариантов заполнить первое место на полке — пять штук. Когда первое место заполнено, то вариантов заполнить второе место остаётся четыре. Всего возможных вариантов заполнения первых двух мест получается $5 \times 4$. Заполняем далее: на третье место претендуют три оставшиеся книги, то есть вариантов, которыми мы можем расставить три книги $5 \times 4 \times 3$. Следуя далее этой логике мы получим, что всего возможных вариантов расставить все пять книг на полке будет $5 \times 4 \times 3 \times 2 \times 1 = 5!$.

Мы получили формулу числа перестановок из $n$ элементов:

\[ P_n = n! \]

То есть любые $n$ объектов можно расставить на $n$ мест $n!$ способами.

9.3.2 Размещения

Теперь представим, что у нас очень маленькая полка, и на ней умещается всего три книги. Сколькими способами мы можем заполнить такую полку, если всего в нашем распоряжении пять книг?

Всего перестановок из пяти книг $5!$, однако в силу того, что на полку умещаются только три первые книги из каждой перестановки, отличных друг от друга вариантов теперь будет меньше. Во сколько раз? В число раз, равно количеству перестановок из тех книг, которые на полку не помещаются. В нашем случае $(5-3)!$. То есть мы можем заполнить нашу полку $\displaystyle \frac{5!}{(5-3)!}$ способами.

Мы получили формулу для подсчета числа размещений из $n$ элементов по $k$:

\[ A_n^k = \frac{n!}{(n-k)!} \]

9.3.3 Сочетания

А теперь задача такова: нам не важно в каком порядке будут стоять книги на полке — нам нужно просто поставить три какие-то книги. Сколько возможно вариантов выбрать три книги из пяти?

Так как мы теперь не учитываем порядок книг, то возможных вариантов будет в $3!$ раз меньше, чем число размещений. Почему? Так как все перестановки этих трёх книг для нас теперь идентичны. Итого, всего вариантов выбрать три книги из пяти $.

Мы получили формулу для подсчета числа сочетаний из $n$ элементов по $k$:

\[ С_n^k = \frac{n!}{k!(n-k)!} \]

Последняя формула на пригодится далее при обсуждении схемы испытаний Бернулли.

9.4 Элементы математического анализа

Из всего матана нам надо уловить два основных концепта — производную и интеграл. Эти и займёмся, захватив попутно немного пределов.

9.4.1 Последовательность

Числовая последовательсность — это последовательность чисел⁶. В общем случае — любых. Она обозначается $(x_n)_{n=1}^\infty$, где $x_n$ — это некоторый элемент последовательности, а верхний и нижний индексы обозначают границы изменения индекса $n$. Например, $\langle 1, -1, 1, -1, \dots \rangle$ — это числовая последовательность, которую можно обозначить $((-1)^n)_{n=1}^\infty$.

Последовательность возникает на некотором множестве чисел. Если на таком множестве определено отношение порядка, то есть элементы этого множества можно сравнивать на «больше-меньше-равно», то можно сформировать монотонную последовательность. Это такая последовательность, которая не возрастает или не убывает. Более того, если существует такой объект (число), к которому элементы последовательности приближаются с ростом номер, то он является…

9.4.2 Предел последовательности

…пределом этой последовательности.

Разберемся на примере. Пусть у нас есть вот такая простенькая последовательность:

\[ \Big(\frac{1}{n}\Big)_{n=1}^\infty = \Big \langle 1, \frac{1}{2}, \frac{1}{3}, \dots \Big \rangle \]

Достаточно очевидно, что каждый следующий её элемент, меньше предыдущего. Отрицательными элементы данной последовательности быть не могут, поэтому кажется, что всё идет к тому, что где-то там последовательность упрётся в ноль.

Формально число $a$ называется пределом последовательности $\{x_n\}$, если для любого положительного числа $\varepsilon$ существует номер $N_\varepsilon$, такой что для любого $n > N_\varepsilon$, выполняется равенство $|x_n - a| < \varepsilon$.

\[ \lim_{n \rightarrow \infty} x_n = a \Leftrightarrow \forall \varepsilon >0 \, \exists N(\varepsilon) \in \mathbb{N}: n \geq N \Rightarrow |x_n - a| < \varepsilon \]

То есть, в случае нашей последовательности мы можем отсутупить на сколь угодно малое число $\varepsilon$ от нуля, и, начиная с какого-то номера, все элементы нашей последовательности окажутся в интервале $(\varepsilon, 0)$. Поэтому

\[ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 \]

9.4.3 Функции

Функции (они же отображения, как мы выяснили выше) устанавливают соответствие между элементами двух множеств. Чаще всего мы имеет дело с числовыми функциями, то есть такими, которые ставят одни числа в соответствие другим. У любой функции есть область определения (множество X) и область значений (множество Y). Сама же функция представляет собой множество упорядоченных пар $(x, y) \in X \times Y$, таких что пары существуют для всех элементов $X$, и если первые элементы пар равны, то равны и их вторые элементы.

9.4.3.1 Дискретные и непрерывные функции

В зависимости от того, каково множество $X$ функции могут быть дискретные и непрерывные. Например, если функция определена на множестве $\mathbb{Z}$, то она будет дискретная, так как между $1$ и $2$ будет пусто.

Если функция определена на множестве $\mathbb{R}$, то она будет непрерывной. Например, функция $f(x) = x^2$ является непрерывной, а также, например, функции $f(x) = \sqrt{x}$ и $f(x) = \log(x)$. Непрерывные функции хороши тем, что они дифференцируемы⁷.

9.4.4 Дифференцируемость функции. Производная

А раз они дифференцируемы, то мы можем взять производную!

Производная — штука очень полезная. Во-первых, она показывает тангенс угла наклона касательной в данной точке, а во-вторых скорость и направление изменения функции в данной точке. На самом деле, что одно, что другое рассказывает нам примерно об одном и том же.

Давайте издалека. Как нам узнать, куда двигается функция в данной точке?

Выберем точку, $x_0$ в которой мы хотим определить, куда и с какой скоростью движется наша функция. В этой точке функция имеет значение $y_0$:

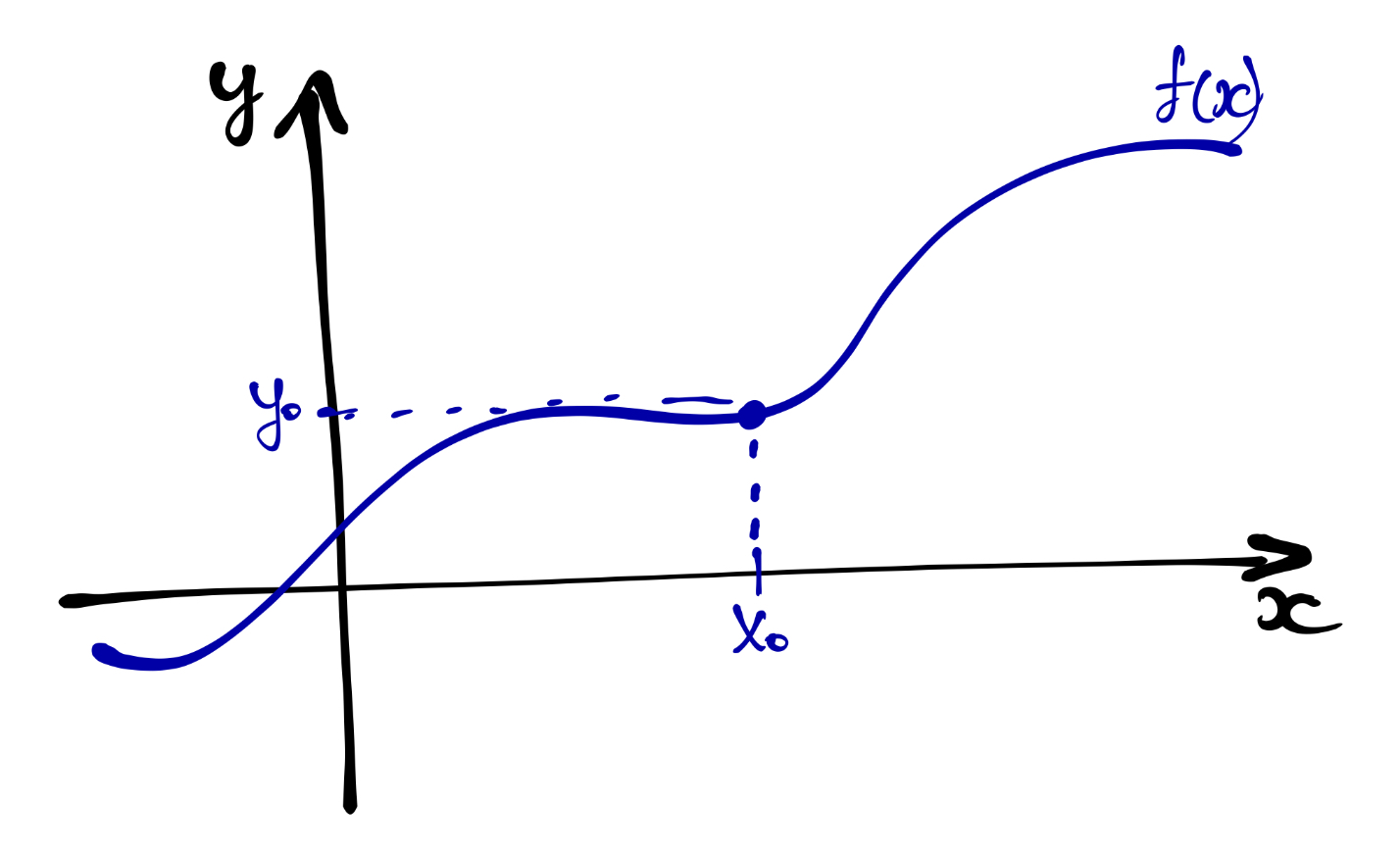
Шагнём на некоторую дистанцию $\Delta x$ вправо (по направлению оси $x$). Назовём эту дистанцию приращением. В точке $x_0 + \Delta x$ фунция будет иметь какое-то значение $y_0 + \Delta y$.

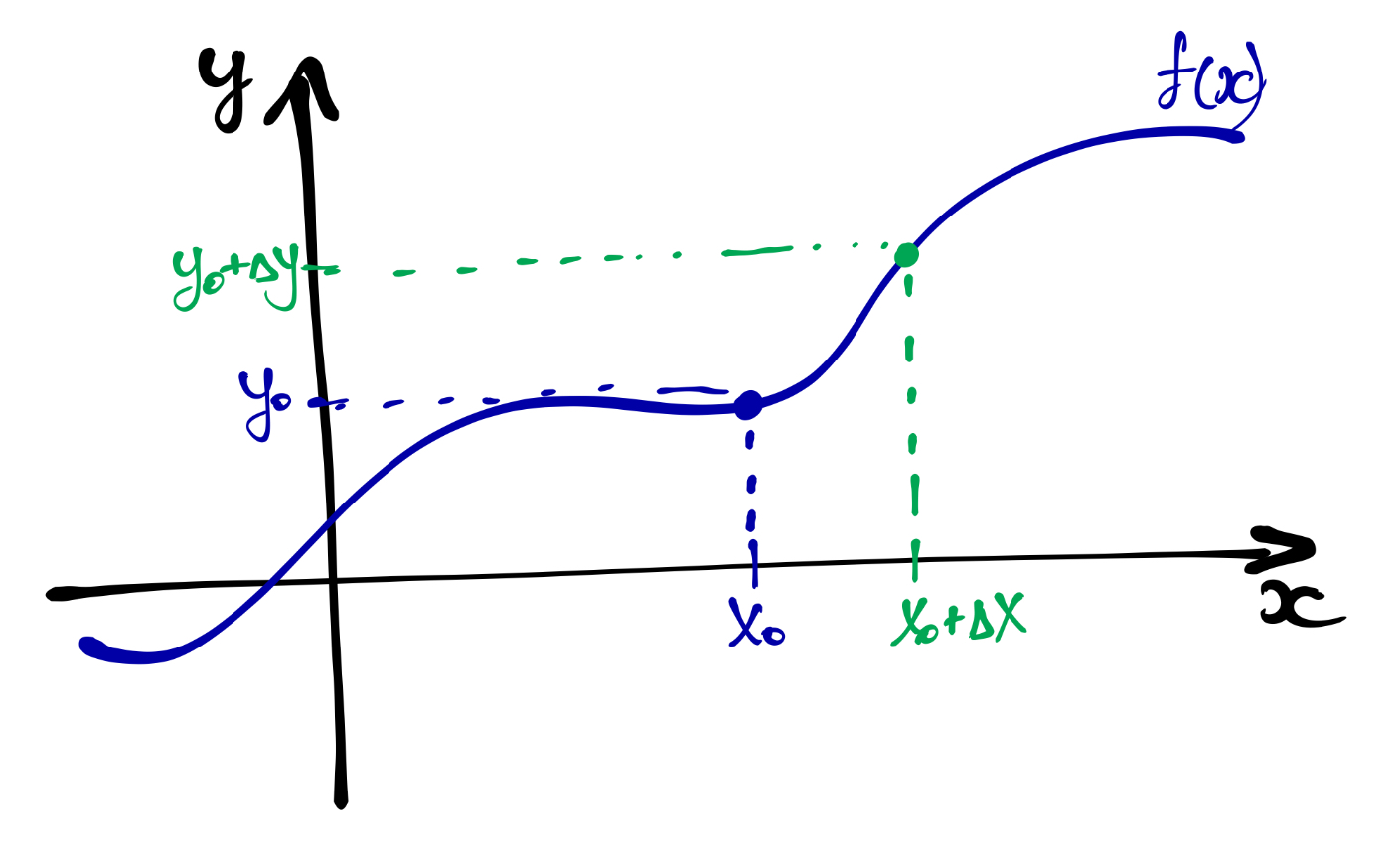
Наша функция движется из точки $(x_0, y_0)$ в точку $(x_0 + \Delta x, y_0 + \Delta y)$. То есть имеем следующий треугольник:

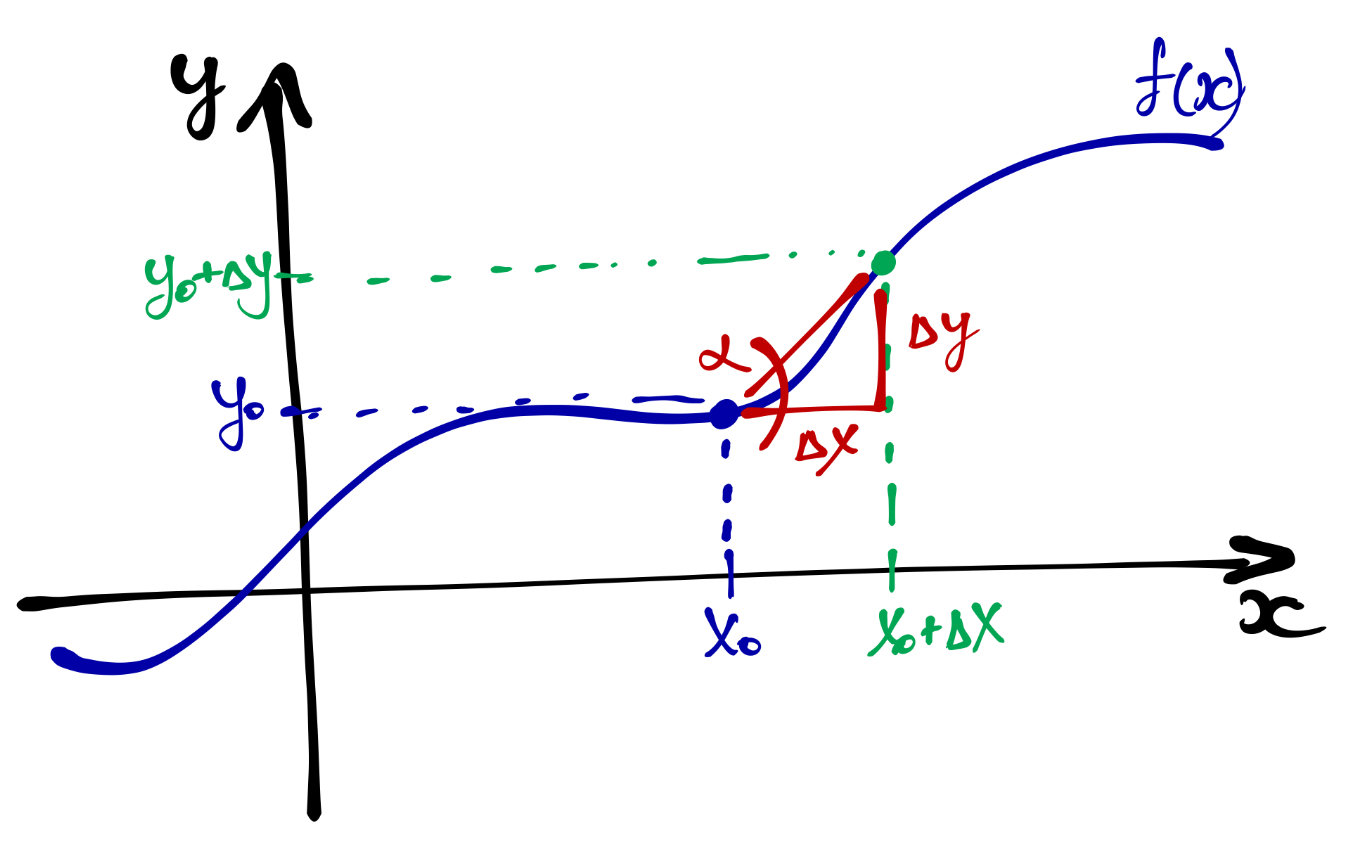
Если мы узнаем, каков угол $\alpha$ — а точнее $\tan \alpha$, потому что так проще — то узнаем, куда движется функция.

\[ \tan \alpha = \frac{\Delta y}{\Delta x} \]

Ну, хорошо. Но мы шагали далеко от точки, которая нас интесует. Если мы будем постепенно уменьшать шаг, то получим последовательность

\[ \tan \alpha_1, \tan \alpha_2, \tan \alpha_3, \dots \]

У этой последовательности есть предел, и если мы его рассчитаем, то как раз и получим значение производной в данной точке.

\[ f'(x_0) = \lim_{\Delta x \rightarrow 0} \frac{\Delta f(x)}{\Delta x} = \frac{df}{dx} (x_0) \]

Очень маленькое приращение обозначается $dx$ (или $df$, если это приращение функции). Вот мы и получили производную.

Можно построить график производной. Это тоже будет функция. Важное свойство этой функции, которое нам понадобится в дальнейшем, заключается в том, что в там, где график производной пересекает ось $x$ — то есть там, где производная равна нулю — на исходной функции случаются точки смены монотонности (то есть точки минимума и максимума).

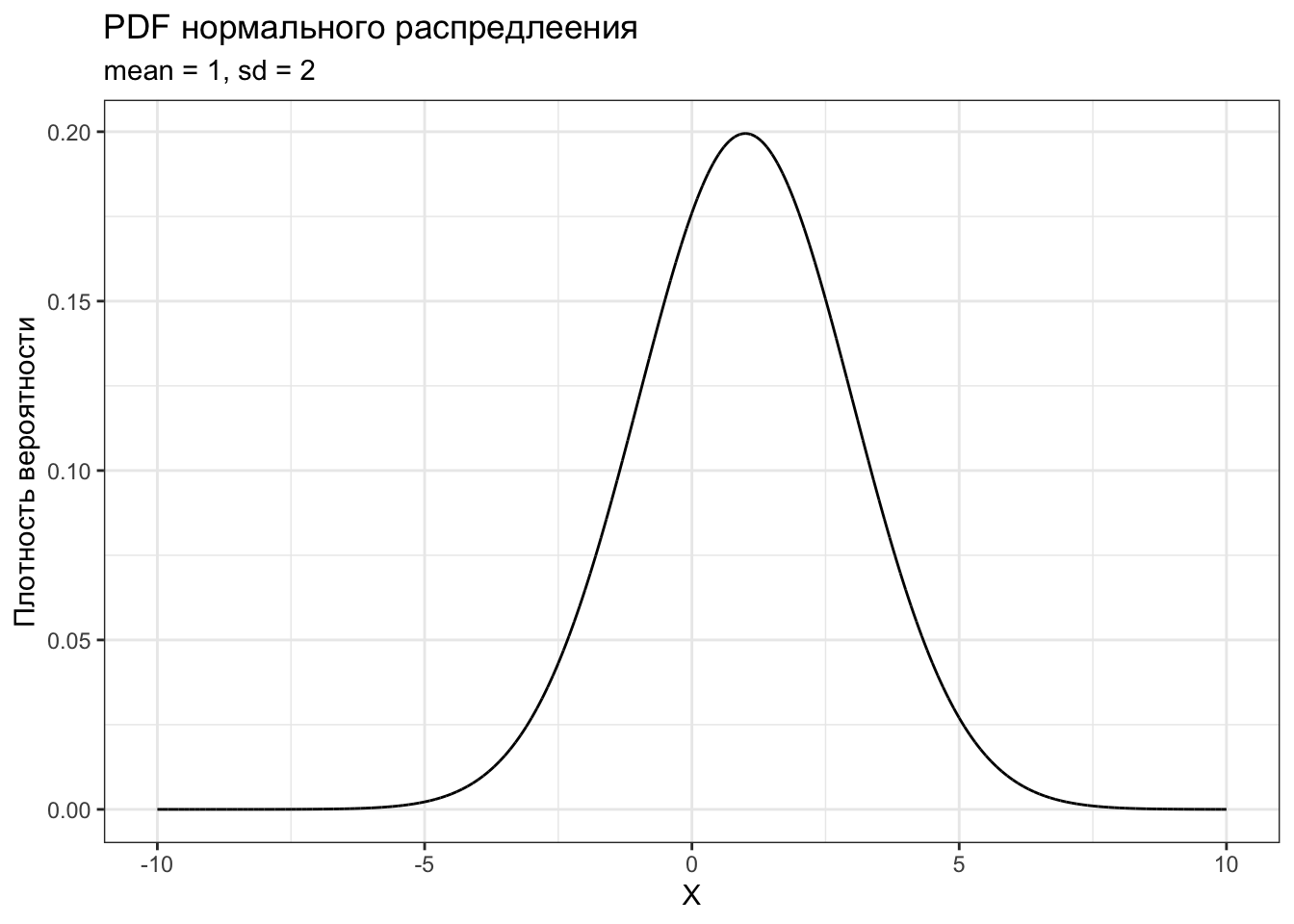
Тут есть таблица производных элементальных функций.

9.4.5 Функции нескольких переменных

Существуют функции не только от одной переменной. Например, можно определить какую-то такую функцию:

\[ z = \cos(x) + \log(|y|) \]

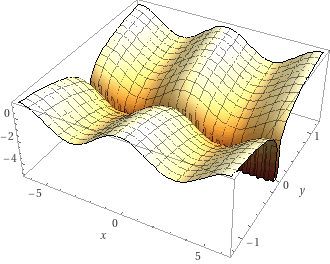
Работают они так же, как и обычные функции, но у них есть важная фича. 👇🏻

9.4.6 Частные производные

Так как у нас теперь несколько переменных, от которых зависит значение функции, мы можем смотреть, как они изменяются по каждой из них в отдельности. Это позволяют сделать частные производные.

Частные производные в целом беруться так же, как и обычные, только мы предполагаем, что все другие переменные, то есть те, по которым мы не берём производную — это константы. Таким образом, мы получаем скорость изменения функции по какой-либо одной переменной.

Например, у нас есть функция

\[ z = \sqrt{x} + y^2 \]

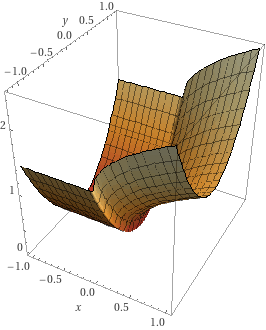
Если нас интересует производная по $x$, то мы предполагаем следующее:

\[ y = \mathrm{const} \Rightarrow y^2 = \mathrm{const} = c \\ \frac{\partial z}{\partial x} = (\sqrt{x} + c)' = (\sqrt{x})' + c' = \frac{1}{2\sqrt{x}} \]

Если же нас интересует производная по $y$, то мы делаем так:

\[ x = \mathrm{const} \Rightarrow \sqrt{x} = \mathrm{const} = c \\ \frac{\partial z}{\partial y} = (y^2 + c)' = (y^2)' + c' = 2y \]

Также вы видите, что частная производная обозначается в помощью символа $\partial$, чтобы она отличалась от полной производной, которая нам не понадобится. :)

9.4.7 Интеграл

Интеграл — штука мощная, но нам он понадобится только с одной стороны. Нам надо будет искать площадь под кривой. Этим и займемся.

Пусть у нас есть знакомая нам функция $y = \sqrt x$. Нам надо найти площадь по ней на отрезке от $0$ до $3$.

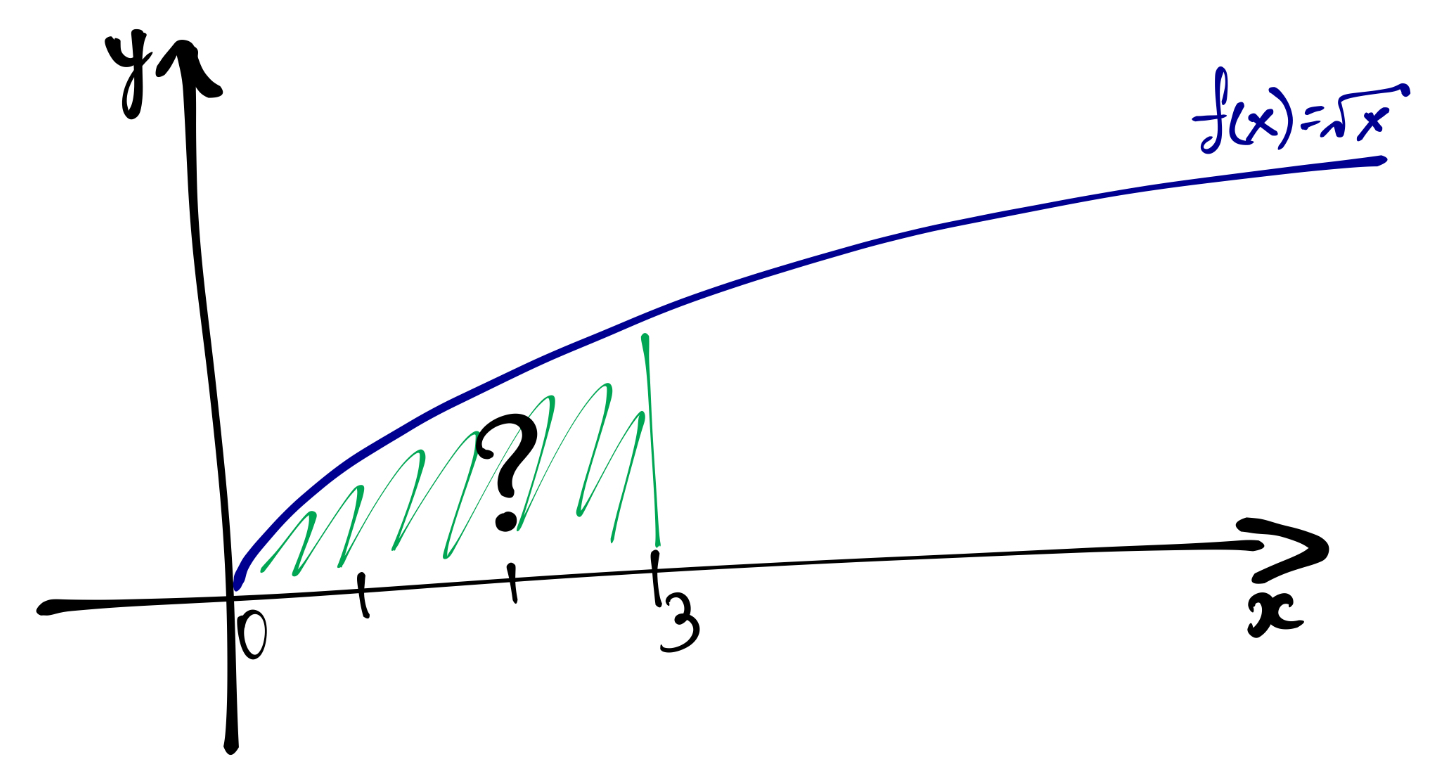
Мы можем разбить этот отрезок на части размером $\Delta x$, а саму площадь на соответствующие прямоугольники. Это нам позволит оценить площадь:

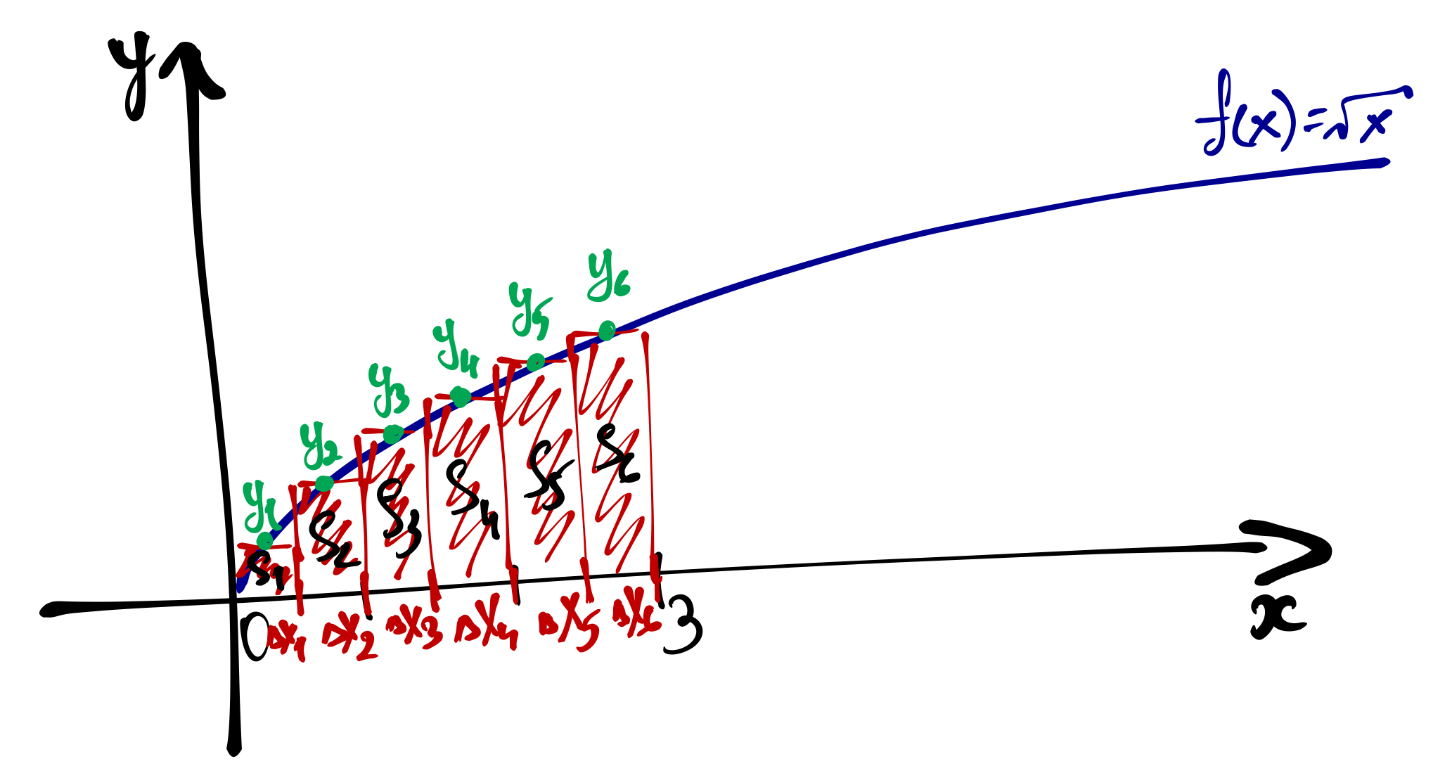
\[ S \approx \sum_{i=1}^n y_i \Delta x_i \]

Ясно, что чем более узкими прямоугольники у нас будут, тем точнее мы будем знать площадь. Снова нам на помощь приходят пределы:

\[ \lim_{\Delta x \rightarrow 0} \sum_{i=1}^n y_1 \Delta x_i = \int_a^b \sqrt x \, dx \]

Такая штука называется определённый интеграл. Определенный он потому, что мы знаем, площадь в каких границах нас интересует. Определённый интеграл — это число.

\[ \int_0^3 \sqrt x \, dx \approx 3.46 \]

integrate(f = sqrt, lower = 0, upper = 3)

## 3.464102 with absolute error < 4e-04

А раз есть определённых интеграл, значит есть и неопределённый. Здесь нам понадобиться вот эта визуализация:

Мы смотрим, как изменяется площадь под графиком некоторой функции $f(x)$ по мере нашего движения по оси $x$, и строим соответствующий график. Этот график и отображает неопределенный интеграл, второй название которого первообразная. Неопределённый интеграл (первообразная) — это функция, причем такая, что её производная равна $f(x)$. Первообразная обозначается $F(x)$. Таким образом, справедливо равенство $F'(x) = f(x)$.

А также справедливо соответствие между определённым и неопредленным интегралом:

\[ \int_a^b f(x)dx = F(b) - F(a) \]

9.5 Элементы линейной алгебры

9.5.1 Что такое матрица?

«Увы, невозможно объяснить, что такое матрица. Ты должен увидеть это сам.»
Морфеус (Матрица, 1999)

Матрица выглядит как таблица чисел, записанных в определенном порядке. Например, вот так:

\[ \boldsymbol{A}= \begin{pmatrix} 1 & 6 & 11 \\ 2 & 7 & 13 \\ 3 & 8 & 15 \\ 4 & 9 & 18 \\ 5 & 0 & 19 \end{pmatrix} \]

В данном случае это прямоугольная матрица $\boldsymbol{A}$. Матрицы обозначаются заглавными буквами (иногда еще и полужирным написанием, чтобы отличать от обычных переменных). Количество строк и столбцов определяет размер матрицы. То есть данная матрица имеет размер 5×3 — $\boldsymbol{A}_{5×3}$. При указании размера сначала указывается количество строк, затем — число столбцов.

Ну, и, собственно, всё. Это и есть матрица.

9.5.2 Откуда берутся матрицы?

Матрицы возникают при решении систем линейных уравнений. Рассмотрим систему.

\[ \begin{cases}a_{11}x_1 + a_{12}x_2 + \ldots + a_{1m}x_m = b_1 \\a_{21}x_1 + a_{22}x_2 + \ldots + a_{2m}x_m = b_2 \\ \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \\a_{n1}x_1 + a_{n2}x_2 + \ldots + a_{nm}x_m = b_n \end{cases} \]

Система состоит из $n$ линейных уравнений относительно $m$ неизвестных. Её можно переписать в матричном виде:

\[ \boldsymbol{A}\boldsymbol{x}= \boldsymbol{b}, \]

где

\[ \boldsymbol{A}= \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1m} \\ a_{21} & a_{22} & \dots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nm} \end{pmatrix} ; \quad \boldsymbol{x}= \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{pmatrix} ; \quad \boldsymbol{b}= \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \]

Здесь мы видим матрицу коэффициентов системы $\boldsymbol{A}$. Размер этой матрицы $n × m$. Также мы видим две особых матрицы $\boldsymbol{x}$ и $\boldsymbol{b}$. Количество столбов у них равно единице. Такие матрицы носят название векторов.

Но ведь мы можем написать вектор всего с одной строкой. Например, некоторый вектор $\boldsymbol{c}$:

\[ \boldsymbol{c}= \begin{pmatrix} c_1 & c_2 & \dots & c_k \end{pmatrix} \]

Для большей точности принята следующая терминология: векторы вида $\boldsymbol{x}$ называют «вектор-столбец», а векторы вида $\boldsymbol{c}$ называют «вектор-строка». Векторы часто также обозначаются полужирным начертанием, чтобы отличать их от отдельных значений.

Так как отдельные столбцы матрица мы можем представить в виде векторов, то матрицу $\boldsymbol{A}$ можно написать еще одним способом: \[ \boldsymbol{A}= \begin{pmatrix} \boldsymbol{A}_1 & \boldsymbol{A}_2 & \dots & \boldsymbol{A}_m \end{pmatrix}, \]

где

\[ \boldsymbol{A}_i = \begin{pmatrix} a_{1i} \\ a_{2i} \\ \vdots \\ a_{ni} \end{pmatrix}, \quad 0<i \leq m \]

Ок, но остается вопрос: почему матричная запись равносильна причной нам записи системы?

Деталь 1

Есть две замечательные матрицы: единичная матрица $\boldsymbol{E}$ (иногда $\boldsymbol{I}$) и нулевая матрица $\boldsymbol{O}$: \[ \boldsymbol{E}= \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \end{pmatrix} ; \quad \boldsymbol{O}= \begin{pmatrix} 0 & 0 & \dots & 0 \\ 0 & 0 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 0 \end{pmatrix} \]

Деталь 2

Матрица размером $n × n$ называется квадратной матрицей.

Квадратная матрица, все элементы которой, кроме стоящих на главной диагонали, равны нулю, называется диагональной матрицей.

9.5.3 Действия с матрицами

9.5.3.1 Сложение матриц

Сложение определено только для матриц одинакового размера.

\[ \boldsymbol{A}_{n×m} + \boldsymbol{B}_{n×m} = \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \dots & a_{1m} + b_{1m} \\ a_{21} + b_{21} & a_{22} + b_{22} & \dots & a_{2m} + b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} + b_{n1} & a_{n2} + b_{n2} & \dots & a_{nm} + b_{nm} \end{pmatrix} \]

Свойства сложения матриц:

$\boldsymbol{A}+ \boldsymbol{B}= \boldsymbol{B}+ \boldsymbol{A}$ (коммутативность)
$(\boldsymbol{A}+ \boldsymbol{B}) + \boldsymbol{C}= \boldsymbol{A}+ (\boldsymbol{B}+ \boldsymbol{C})$ (ассоциативность)
$\boldsymbol{A}+ \boldsymbol{O}= \boldsymbol{A}$ (существование нулевого элемента)
$\boldsymbol{A}+ (-\boldsymbol{A}) = \boldsymbol{O}$ (существование противоположного элемента)

Все, описанное выше, справедливо для векторов.

9.5.3.2 Умножение матрицы на число

Умножение на вещественное число определено для любой матрицы $n × m$.

\[ \lambda \boldsymbol{A}= \begin{pmatrix} \lambda a_{11} & \lambda a_{12} & \dots & \lambda a_{1m} \\ \lambda a_{21} & \lambda a_{22} & \dots & \lambda a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ \lambda a_{n1} & \lambda a_{n2} & \dots & \lambda a_{nm} \end{pmatrix}, \; \forall \lambda \in \mathbb{R} \]

Свойства умножения матрицы на число:

$1 \cdot \boldsymbol{A}= \boldsymbol{A}$
$-1 \cdot \boldsymbol{A}= -\boldsymbol{A}$
$\lambda(\mu \boldsymbol{A}) = (\lambda \mu) \boldsymbol{A}$ (ассоциативность)
$(\lambda + \mu) \boldsymbol{A}= \lambda \boldsymbol{A}+ \mu \boldsymbol{A}$ (дистрибутивность)
$\lambda (\boldsymbol{A}+ \boldsymbol{B}) = \lambda \boldsymbol{A}+ \lambda \boldsymbol{B}$ (дистрибутивность)

Все, описанное выше, справедливо для векторов.

9.5.4 Скалярное произведение векторов

Скаларное произведение определено для векторов одинаковой размерности как сумма произведений их соответствующих координат.

\[ \boldsymbol{a}= \begin{pmatrix} a_1 & a_2 & \dots & a_n \end{pmatrix} \\ \boldsymbol{b}= \begin{pmatrix} b_1 & b_2 & \dots & b_n \end{pmatrix}\\ \] \[ \boldsymbol{a}\cdot \boldsymbol{b}= a_1 b_1 + a_2 b_2 + \dots + a_n b_n \]

9.5.5 Векторное произведение векторов

мы рассматривать не будем :)

9.5.6 Произведение матриц (матричное умножение)

Ну, вот и начался треш.

Умножение определено для матриц $\boldsymbol{A}_{n × k}$ и $\boldsymbol{B}_{k × m}$, то количество столбцов матрицы, стоящей слева от знака умножения, должно быть равно количество строк матрицы, стоящей справа от знака умножения.

Произведением матрицы $\boldsymbol{A}_{n × k}$ на матрицу $\boldsymbol{B}_{k × m}$ называется матрица $\boldsymbol{C}_{n × m}$, элемент которой $c_{ij}$ равен скалярному произведению $i$-го вектора-строки матрицы $\boldsymbol{A}$ и $j$-го вектора-столбца матрицы $\boldsymbol{B}$.

Пусть \[ \boldsymbol{A}= \begin{pmatrix} \boldsymbol{a}_1 \\ \boldsymbol{a}_2 \\ \vdots \\ \boldsymbol{a}_n \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1k} \\ a_{21} & a_{22} & \dots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nk} \end{pmatrix}, \\ \boldsymbol{B}= \begin{pmatrix} \boldsymbol{b}_1 & \boldsymbol{b}_2 & \dots \boldsymbol{b}_m \end{pmatrix} = \begin{pmatrix} b_{11} & b_{12} & \dots & b_{1m} \\ b_{21} & b_{22} & \dots & b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{k1} & b_{k2} & \dots & b_{km} \end{pmatrix} \]

Тогда,

\[ \boldsymbol{A}\times \boldsymbol{B}= \begin{pmatrix} \boldsymbol{a}_1 \cdot \boldsymbol{b}_1 & \boldsymbol{a}_1 \cdot \boldsymbol{b}_2 & \dots & \boldsymbol{a}_1 \cdot \boldsymbol{b}_m \\ \boldsymbol{a}_2 \cdot \boldsymbol{b}_1 & \boldsymbol{a}_2 \cdot \boldsymbol{b}_2 & \dots & \boldsymbol{a}_2 \cdot \boldsymbol{b}_m \\ \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{a}_n \cdot \boldsymbol{b}_1 & \boldsymbol{a}_n \cdot \boldsymbol{b}_2 & \dots & \boldsymbol{a}_n \cdot \boldsymbol{b}_m \\ \end{pmatrix} = \\ = \begin{pmatrix} (a_{11} b_{11} + a_{12} b_{21} + \dots + a_{1k}b_{k1}) & (a_{11} b_{12} + a_{12} b_{22} + \dots + a_{1k}b_{k2}) & \dots & (a_{11} b_{1m} + a_{12} b_{2m} + \dots + a_{1k}b_{km}) \\ (a_{21} b_{11} + a_{22} b_{21} + \dots + a_{2k}b_{k1}) & (a_{21} b_{12} + a_{22} b_{22} + \dots + a_{2k}b_{k2}) & \dots & (a_{21} b_{1m} + a_{22} b_{2m} + \dots + a_{2k}b_{km}) \\ \vdots & \vdots & \ddots & \vdots \\ (a_{n1} b_{11} + a_{n2} b_{21} + \dots + a_{nk}b_{k1}) & (a_{n1} b_{12} + a_{n2} b_{22} + \dots + a_{nk}b_{k2}) & \dots & (a_{n1} b_{1m} + a_{n2} b_{2m} + \dots + a_{nk}b_{km}) \end{pmatrix} = \\ = \begin{pmatrix} c_{11} & c_{12} & \dots & c_{1m} \\ c_{21} & c_{22} & \dots & c_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \dots & c_{nm} \end{pmatrix} = \boldsymbol{C} \]

\[ c_{ij} = \sum_{t=1}^k a_{it} b_{tj} \]

Вот так вот.

Cвойства произведения матриц:

$\boldsymbol{A}(\boldsymbol{B}\boldsymbol{C}) = (\boldsymbol{A}\boldsymbol{B}) \boldsymbol{C}$ (ассоциативность)
$\lambda (\boldsymbol{A}\boldsymbol{B}) = (\lambda \boldsymbol{A}) \boldsymbol{B}= (\lambda \boldsymbol{B}) \boldsymbol{A}$ (ассоциативность)
$\boldsymbol{A}(\boldsymbol{B}+ \boldsymbol{C}) = \boldsymbol{A}\boldsymbol{B}+ \boldsymbol{A}\boldsymbol{C}$ (дистрибутивность)
$(\boldsymbol{A}+ \boldsymbol{B}) \boldsymbol{C}= \boldsymbol{A}\boldsymbol{C}+ \boldsymbol{B}\boldsymbol{C}$ (дистрибутивность)
$\boldsymbol{A}\boldsymbol{B}\neq \boldsymbol{B}\boldsymbol{A}$ (отсутствие коммутативности)
$\boldsymbol{E}\boldsymbol{A}= \boldsymbol{A}; \, \boldsymbol{A}\boldsymbol{E}= \boldsymbol{A}$ (умножение на единичный элемент)
$\boldsymbol{O}\boldsymbol{A}= \boldsymbol{O}; \, \boldsymbol{A}\boldsymbol{O}= \boldsymbol{O}$ (умножение на нулевой элемент)
$\boldsymbol{A}\boldsymbol{A}^{-1} = \boldsymbol{A}^{-1} \boldsymbol{A}= \boldsymbol{E}$ (умножение на обратную матрицу — только для некоторых квадратных матриц)

Матричное умножение определено для векторов-столбцов (матриц-столбцов) и векторов-строк (матриц-строк) и выполняется по тем же правилам.

9.5.7 Транспонирование матрицы

В матрице строки и столбцы можно поменять местами — получится транспонированная матрица.

\[ \boldsymbol{A}= \begin{pmatrix} \boldsymbol{a}_1 \\ \boldsymbol{a}_2 \\ \vdots \\ \boldsymbol{a}_n \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1k} \\ a_{21} & a_{22} & \dots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nk} \end{pmatrix} \] \[ \boldsymbol{A}^\mathrm{T}= \begin{pmatrix} \boldsymbol{a}_1 & \boldsymbol{a}_2 & \dots & \boldsymbol{a}_n \end{pmatrix} = \begin{pmatrix} a_{11} & a_{21} & \dots & a_{n1} \\ a_{12} & a_{22} & \dots & a_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1k} & a_{2k} & \dots & a_{nk} \end{pmatrix} \] Транспонированная матрица будет иметь размер $k × n$.

9.5.8 Детерминант и обратная матрица

Детерминант (определитель) $\det \boldsymbol{A}, \; |\boldsymbol{A}|, \Delta \boldsymbol{A}$ — величина, которая может быть вычислена и поставлена в однозначное соответствие квадратной матрице. Он «определяет» свойства матрицы, в том числе, её обратимость.

Детерминант матрицы из одного элемента равен этому элементу:

\[ \det \begin{pmatrix} a_{11} \end{pmatrix} = a_{11} \] Детерминант матрицы $2×2$ вычисляется следующим образом — это разность произведений элементов главной⁸ и побочной⁹ диагоналей:

\[ \det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = a_{11} a_{22} - a_{12} a_{21} \]

Вычисление дереминанта матрицы произвольного размера $n × n$ требует введения ещё пары определений.

Дополнительный минор $M_{ij}$ матрицы $\boldsymbol{A}$ — это дереминант матрицы, полученной из матрицы $\boldsymbol{A}$ путём вычеркивания $i$-ой строки и $j$-го столбца.

Алгебраическое дополнение элемента $a_{ij}$ матрицы $\boldsymbol{A}$ — число, которое получается при умножении минора $M_{ij}$ на $(-1)^{i+j}$:

\[ A_{ij} = (-1)^{i+j} M_{ij} \]

Детерминант матрицы произвольного размера $n×n$ вычисляется так¹⁰:

\[ \det \boldsymbol{A}_{n×n} = \sum_{j=1}^n (-1)^{1 + j} a_{1j} M_{1j} = \sum_{j=1}^n a_{1j}A_{1j}, \] где $M_{1j}$ — дополнительный минор к элементу $a_{1j}$.

Но жизнь упрощается, когда есть R:

A <- matrix(sample(20:30, 9), nrow = 3)
det(A) # так вычисляется детерминант матрицы

## [1] 334

Если матрица квадратная и её детерминант не равен нулю, то для данной матрицы $\boldsymbol{A}$ существует обратная ей $\boldsymbol{A}^{-1}$, которая обаладет следующим свойством:

\[ \boldsymbol{A}\boldsymbol{A}^{-1} = \boldsymbol{E} \]

Детерминант матрицы равен нулю, в частности, если её столбцы линейно зависимы, то есть значения одного можно линейно выразить через значения другого. Например,

B <- matrix(c(1, 2, 3,
              2, 5, 6,
              3, 8, 9), nrow = 3)
det(B)

## [1] 0

Для такой матрицы обратной ей матрицы не существует.

9.5.9 След матрицы

След матрицы — сумма элементов (квадратной) матрицы, стоящих на главной¹¹ диагонали.

\[ \mathrm{tr}(\boldsymbol{A}) = \sum_i a_{ii} \]

О нём мы чуть-чуть вспомним, когда будем обсуждать ковариационные матрицы.

В R нет специальной функции, которая вычисляет след матрицы. Давайте её напишем!

Функция должна принимать на вход матрицу, проверять, является ли матрица квадратной, и, если да, то возвращать значение следа матрицы, если нет, то печатать в консоль «матрица не является квадратной».

Подсказка: ?diag

B <- matrix(sample(1:100, 25), nrow = 5)
C <- matrix(sample(1:100, 12), nrow = 4)
tr(B)

## [1] 159

tr(C)

## [1] "\u043c\u0430\u0442\u0440\u0438\u0446\u0430 \u043d\u0435 \u044f\u0432\u043b\u044f\u0435\u0442\u0441\u044f \u043a\u0432\u0430\u0434\u0440\u0430\u0442\u043d\u043e\u0439"

Дано: \[ \boldsymbol{A}= \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix} ; \quad \boldsymbol{B}= \begin{pmatrix} 5 & 6 & 7 \\ 8 & 9 & 0 \end{pmatrix} ; \\ \boldsymbol{a}= \begin{pmatrix} 11 & 22 & 33 \end{pmatrix}; \quad \boldsymbol{b}= \begin{pmatrix} 101 \\ 102 \\ 103 \end{pmatrix}; \]

Вычислить:

$\boldsymbol{A}\times \boldsymbol{B}$;
$\boldsymbol{B}\times \boldsymbol{A}$;
$\boldsymbol{a}\times \boldsymbol{b}$;
$\boldsymbol{b}\times \boldsymbol{a}$;
$\boldsymbol{a}\times \boldsymbol{a}^\mathrm{T}$

Чтобы проверить ответ, введите в соответствующее поле значения элементов матрицы построчно. Элементы одной строки разделяйте пробелами, строки разделяйте [только] запятыми.

Обсуждение критериев объективности мы оставим за рамками этого курса и постулируем, что мы их как-то хотя бы интуитивно пониманием. Для некоторой концептуальной рамки обозначим следующее: мы говорим об объективной связи между предметами, если (1) определённым предметам (или индивидам) присущи определённые признаки и если (2) определённым признакам свойственны определённые признаки.↩
Есть в другие подходы к определению истинности высказываний — таковый различные виды многозначной логики. Но они не-необходимы нам для целей курса, поэтому оставим их за бортом.↩
Этот факт часто используется при доказательстве всяких невозможных математических утверждений, когда изначально принимается неверная посылка, но это не очевидно.↩
В теории множеств натуральные числа начинаются с нуля. Если нас интересуют натуральные числа без нуля, то мы будем использовать обозначение $\mathbb{Z}_+$, то есть целые положительные числа.↩
По умолчанию считаем, что $x \in \mathbb{R}$.↩
Некотрые определения математики заставляют тебя задуматься о том, что ты ещё не до конца постиг дзен абстрактной науки…↩
Хотя и не все. Непрерывность является необходимым, но недостаточным условием для дифференцируемости.↩
Та, которая идёт слева сверху вправо вниз.↩
Та, которая идёт справа сверху влево вниз.↩
Эта формула называется разложением по строке. Есть и другие ↩
Та, которая идёт слева сверху вправо вниз.↩