18 Множественная линейная регрессия
Связи двух переменных — это, конечно, хорошо. Но на практике нас обычно интересуют более сложные закономерности. Их, как мы говорили, можно изучать и корреляционным анализом, но регрессия делает это как-то более элегантно.
18.1 Множественная линейная регрессия с количественными предикторами
18.1.1 Математическая модель
Итак, мы хотим изучить влияние1 нескольких независимых переменных (предикторов) на нашу зависимую (целевую) переменную. Модель в общем-то меняется не сильно — просто добавляется ещё одно слагаемое:
\[ y_i = b_0 + b_1 x_{i1} + b_2 x_{i2} + e_i \]
Теперь нам надо подбирать не два коэффициента, а три. Но, на самом деле, это ничего не меняет.
18.1.2 Подбор модели
Конечно, если мы будем пытаться решить задачу аналитически, то там будут определённые изменения. Однако мы познакомились с матричными вычислениями и можем обратиться к ним.
В матричном виде модель будет записываться следующим образом:
\[ \boldsymbol{y}= \boldsymbol{X}\boldsymbol{b}+ \boldsymbol{e}, \] где \(\boldsymbol{y}\) — всё ещё вектор нашей зависимой переменной, \(\boldsymbol{X}\) — всё ещё матрица независимых переменных, \(\boldsymbol{b}\) — всё ещё вектор коэффициентов модели, а \(\boldsymbol{e}\) — вектор ошибок (остатков) модели.
Отличие будет в том, как организованы внутри \(\boldsymbol{X}\) и \(\boldsymbol{b}\):
$$ = \begin{pmatrix} 1 & x_{11} & x_{12} \ 1 & x_{21} & x_{22} \ 1 & x_{31} & x_{32} \ & & \ 1 & x_{n1} & x_{n2} \end{pmatrix};
\begin{pmatrix} b_0 \ b_1 \ b_2 \end{pmatrix} $$
Вычисление же коэффициентов будет осуществляться абсолютно аналогично простой линейной регрессии:
\[ \boldsymbol{b}= (\boldsymbol{X}^\mathrm{T}\boldsymbol{X})^{-1}\boldsymbol{X}^\mathrm{T}\boldsymbol{y} \]
Ясно, что не важно, сколько предикторов будет содержать модель — вычисление коэффициентов будет работать одинаково. Однако по сравнению с простой линейной моделью здесь есть одна важная особеность.
18.1.2.1 Проблема мультиколлинеарности
Предикторы могут быть связаны не только с целевой перемненой, но и друг с другом, что обуславливает проблему мультиколлинеарности.
В чем она заключается? Посмотрим ещё раз на формулу выше, которая нам позволяет вычислить параметры модели: в ходе вычислений мы берем обратную матрицу. Если наши предикторы сильно коррелируют друг с другом (\(\geq 0.8\)), то в нашей матрице возникают линейно зависимые столбцы, а значит обратная матрица не будет существовать.
Чем это чревато? В случае абсолютно линейной связи коэффициент модели просто не вычислится — в аутпуте будет NA. Как правило, это намёк на то, чтобы проверить данные — возможно, у вас есть одна и та же переменная, записанная по-разному (например, рост в метрах и сантиметрах). В случае высоких (но меньших единицы) корреляций проблема подбора коэффициентов решается с помощью методов численной оптимизации, однако это может приводить к смещённым оценкам коэффициентов модели, а также большим ошибкам в оценках коэффициентов.
Поэтому с мультиколлинеарностью надо бороться. Вариантов существует много. Наиболее часто используемые: исключение коллинеарных переменных из модели, метод служебной регресии, методы уменьшения размерности (кластерный анализ, PCA и др.).
18.1.2.2 Подбор коэффициентов модели в R
Подбор модели осуществляется с помощью той же самой функции lm(), только в данном случае немного изменяется запись модели. Другие предикторы перечистяются через символ +, как и в математической записи модели.
Допустим, мы хотим учесть в модели [из прошлой главы] не только возраст, но и рост ребенка в предсказании ОФВ. Построим такую модель:
##
## Call:
## lm(formula = FEV ~ Age + Height, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.50533 -0.25657 -0.01184 0.24575 2.01914
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.610466 0.224271 -20.558 < 2e-16 ***
## Age 0.054281 0.009106 5.961 4.11e-09 ***
## Height 0.109712 0.004716 23.263 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4197 on 651 degrees of freedom
## Multiple R-squared: 0.7664, Adjusted R-squared: 0.7657
## F-statistic: 1068 on 2 and 651 DF, p-value: < 2.2e-16Как мы видим, аутпут функции summary() практически не отличается от простой линейной регрессии, только угловых коэффициента у нас теперь два, а не один.
18.1.3 Оценка качества модели
Качество модели оценивается аналогично простой линейной регрессии.
Прежде всего, мы смотрим на F-статистику и p-value, рассчитанный для неё. Если p-value меньше конвенционального значения 0.05, то мы делаем вывод о том, что модель в целом статистически значима.
Далее обращаем внимание на \(R^2\), а лучше сразу на \(R^2_{\mathrm{adj}}\) — скорректированный коэффициент детерминации. Почему на него? Так как в нашей модели теперь несколько предикторов, то скорректированный [на количество предикторов] коэффициент детерминации для нас более информативен. В частности, по его значениям мы можем сравнивать модели с разным количеством предикторов. Как он корректируется? Вот так:
\[ R^2_{\mathrm{adj}} = 1 - (1 - R^2)\frac{n-1}{n-p} \]
После оценки информативности модели мы переходим к тестированию значимости отдельных предикторов — и здесь тоже всё аналогично простой линейной регрессии. Есть оценки значений коэффициентов, есть их стандатные ошибки, есть значение t-теста и p-values, рассчитанные для них. Со всем этим мы уже знакомы.
18.1.4 Диагностика модели
18.1.4.1 Исследование мультиколлинеарности
Но если мы на секунду задумаемся… Мы ввели в модель предиктор «рост», который несомненно связан с ОФВ. Однако он также связан и с возрастом! А не принесли ли мы в нашу модель коллинеарных предикторов?
На этапе разведочного анализа при наличии большого числа предикторов полезно посмотреть на корреляционную матрицу предикторов — что с чем связано. В нашем случае мы можем просто посчитать значение корреляции, так как у нас предикторов сейчас всего два:
## [1] 0.7919436Ожидаемо высокая корреляция. Если корреляция предикторов друг с другом 0.8 и выше — повод задуматься о мультиколлинеарности. У нас значение довольно близкое. Продолжим анализ.
Для того, чтобы выявить, есть ли таки у нас проблема мультикоолинеарности, или мы радостные и довольные можем наслаждаться результатами моделирования, необходимо вычислить коэффициент вздутия дисперсии (variance inflation factor, VIF). Чтобы его вычислить, проводятся следующие операции:
- пусть у нас есть модель \(y = b_0 + b_1 x_1 + b_2 x_2 + \dots + b_m x_m + e\)
- строиться линейная регрессия, в которой один из предикторов регрессируется всеми другими. Например, для первого предиктора:
\[ x_1 = \alpha_0 + \alpha_2 x_2 + \dots \alpha_m x_m \]
- вычисляется коэффициент детерминации для данной модели \(R_i\)
- вычисляется VIF для коэффциента \(b_i\):
\[ \mathrm{VIF}_i = \frac{1}{1 - R^2_i} \]
Все эти вычисления реализованы в функции vif() из пакета car:
## Age Height
## 2.682221 2.682221Пороговым значением для вынесение вердикта о наличии мультиколлинеарности считается 3 (иногда 2). Мы этот вердикт всё же вынесем, и будем с мультиколлинеарностью бороться.
18.1.5 Доработка модели
Как уже отмечалось выше, способов борьбы с мультиколлинеарностью существует несколько. Сейчас мы рассмотрим метод служебной регрессии.
В чём логика этого метода? Наши предикторы связаны друг с другом, но всё же корреляция меньше единицы (что так-то ожидаемо и логично). То есть, часть изменчивости роста может быть объяснена изменчивостью возраста, а часть, конечно же, останется случайной изменчивостью. Звучит как регрессия, не так ли?
Итак, мы можем построить служебную регрессионную модель, которая учтёт часть извенчивости роста, связанную с возрастом — будем считать возраст основным предиктором для нашей главной модели. Всё то, что возрастом объяснено не будет, составит остатки модели служебной регрессии, которые мы сможем внести как предиктор в модель.
Давайте по порядку. Строим служебную регрессию:
Записываем остатки модели в новую переменную датасета:
Заменяем в главной модели рост на «остатки по росту»:
##
## Call:
## lm(formula = FEV ~ Age + resHeight, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.50533 -0.25657 -0.01184 0.24575 2.01914
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.431648 0.057606 7.493 2.2e-13 ***
## Age 0.222041 0.005560 39.934 < 2e-16 ***
## resHeight 0.109712 0.004716 23.263 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4197 on 651 degrees of freedom
## Multiple R-squared: 0.7664, Adjusted R-squared: 0.7657
## F-statistic: 1068 on 2 and 651 DF, p-value: < 2.2e-16Коэффициенты, конечно, получились другие, но модель осталась статистически значима, более того, остатки служебной регрессии в качестве предиктора тоже оказались статистически значимы — значит есть зависимость ОФВ от той изменчивости роста, которая не объясняется возрастом.
И самое главное, что больше нет мультиколлинеарности:
## Age resHeight
## 1 1Для множественной линейной регрессии также можно строить диагностические графики, которые будут интерпретироваться аналогично графика простой линейной регрессии. Например, для модели model2 графики будут выглядеть так:
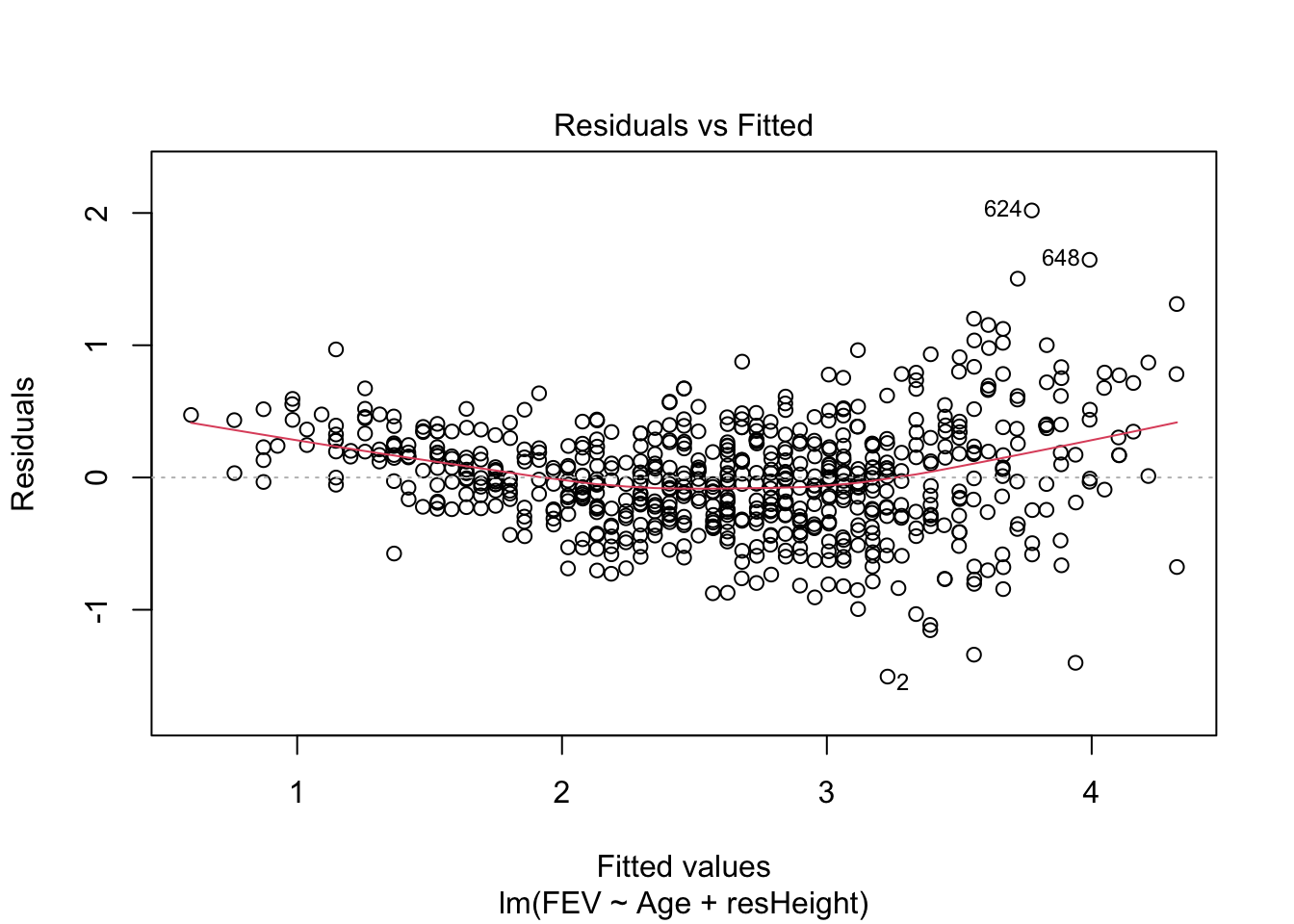
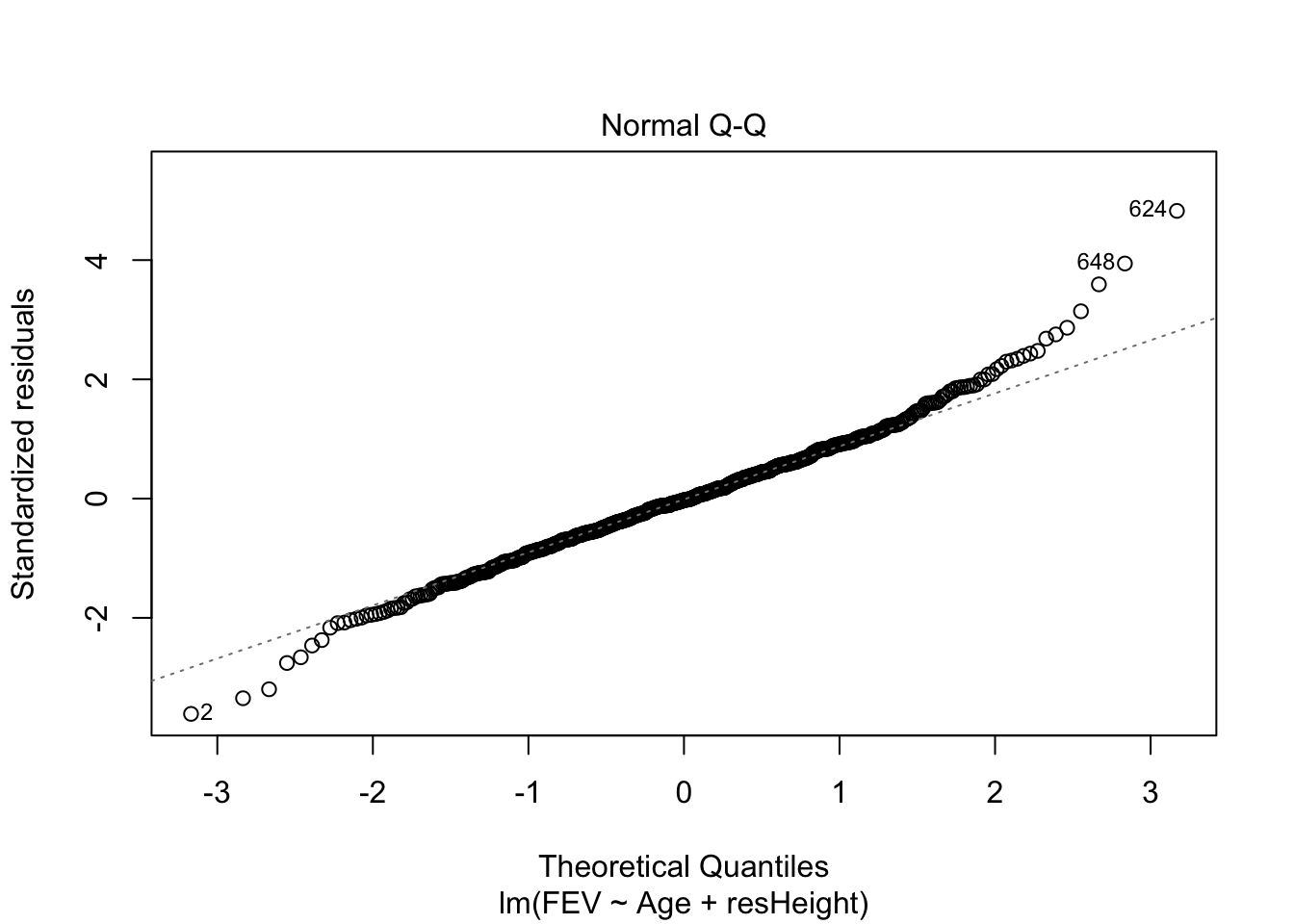
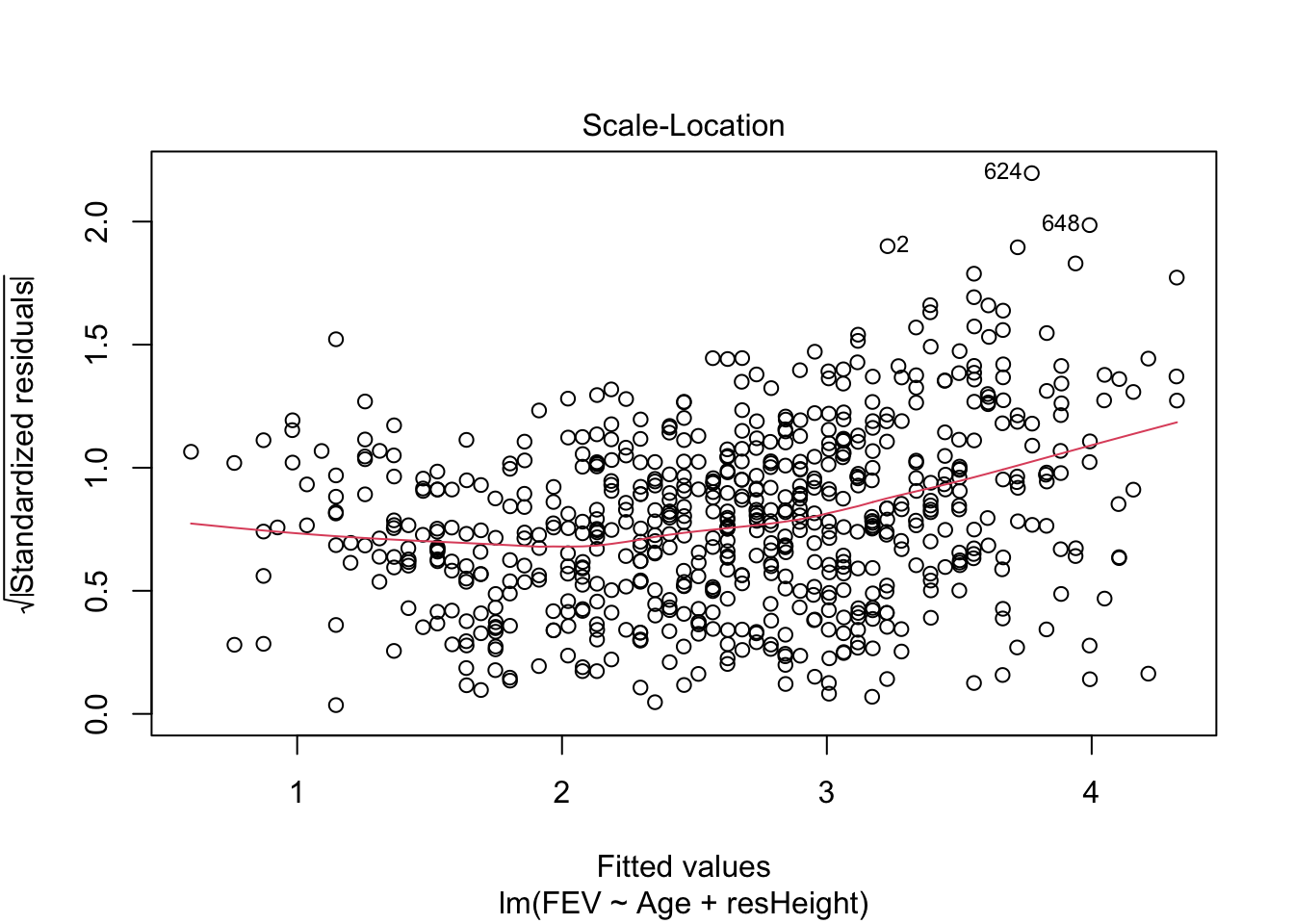
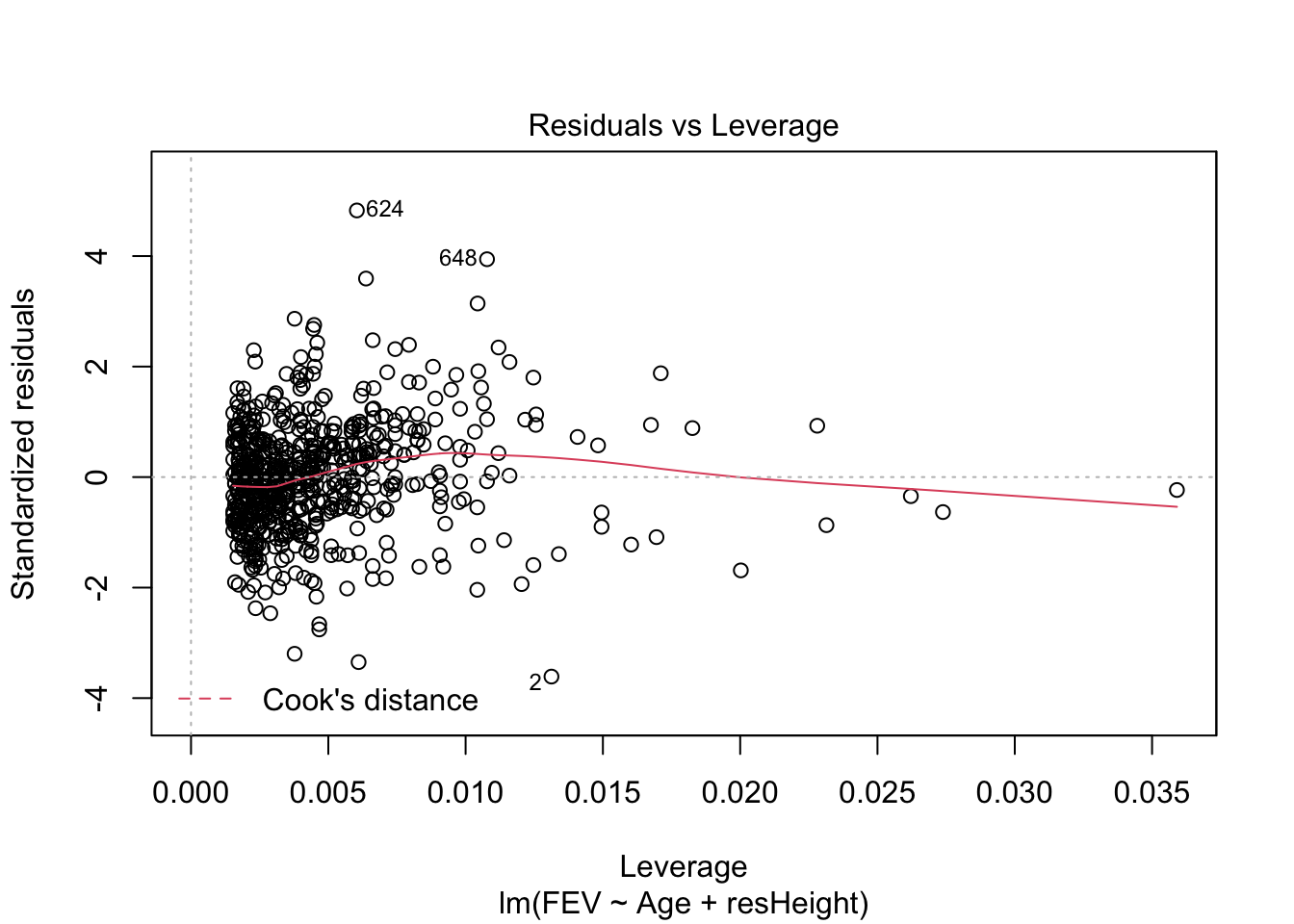

Оцените, стала ли модель лучше после включения в неё второго предиктора. Сравните model2 и model из предыдущей главы.
18.2 Множественная линейная регрессия с количественными и категориальными предикторами
Когда мы имеем дело с количественными предикторами, то всё более-менее ясно — есть зависимость между двумя количественными переменными, описываемая прямой. А что делать, если среди предикторов появляются категориальные переменные?
Посмотрим на датасет, с которым мы работаем, внимательно:
## tibble [654 × 7] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ ID : num [1:654] 301 451 501 642 901 ...
## $ Age : num [1:654] 9 8 7 9 9 8 6 6 8 9 ...
## $ FEV : num [1:654] 1.71 1.72 1.72 1.56 1.9 ...
## $ Height : num [1:654] 57 67.5 54.5 53 57 61 58 56 58.5 60 ...
## $ Sex : chr [1:654] "Female" "Female" "Female" "Male" ...
## $ Smoker : chr [1:654] "Non" "Non" "Non" "Non" ...
## $ resHeight: Named num [1:654] -2.72 9.31 -2.16 -6.72 -2.72 ...
## ..- attr(*, "names")= chr [1:654] "1" "2" "3" "4" ...
## - attr(*, "spec")=
## .. cols(
## .. ID = col_double(),
## .. Age = col_double(),
## .. FEV = col_double(),
## .. Height = col_double(),
## .. Sex = col_character(),
## .. Smoker = col_character()
## .. )Есть две тестовые переменые: Smoker и Sex.
##
## Current Non
## 65 589##
## Female Male
## 318 336Они категориальные. Вполне можно ожидать, что, например, у курящих и некурящих ОФВ будет различаться, так как это показатель косвенно свидетельствующий о состоянии бронхиального дерева. Как включить это в модель?
18.2.1 Математическая модель
С точки зрения влияние категориального предиктора на целевую переменную будет выражаться в различном базовом уровне, то есть intercept, для разных категорий наблюдений. В модели это фиксируется так:
\[ y_i = b_0 + b_1 I_1 + b_2 x_2 + b_3 x_2 \]
В данном случае представлена модель с одним категориальным (\(I_1\)) и двумя количественными (\(x_1\), \(x_2\)) предикторами.
Переменная \(I\) — это переменная индикатор, которая обладает следующим свойством:
- \(I_1 = 0\), если наблюдение относится к категории 1,
- \(I_1 = 1\), если наблюдение относится к категории 2.
Таким образом, у нас получается как бы две модели в одной:
- для наблюдений категории 1 модель принимает следующий вид: \(y_i = b_0 + b_2 x_2 + b_3 x_2\),
- а для наблюдений категории 2 вот такой: \(y_i = (b_0 + b_1) + b_2 x_2 + b_3 x_2\).
Коэффициент \(b_1\) показывает разницу в базовых уровнях между двумя категориями (группами) наблюдений.
18.2.2 Подбор модели
С точки зрения подбора модели кардинальных изменений не происходит:
А вот на аутпут summary() придётся посмотреть чуть внимательнее:
##
## Call:
## lm(formula = FEV ~ Age + resHeight + Smoker, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.50182 -0.26305 -0.01882 0.24989 1.98535
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.28752 0.09729 2.955 0.00324 **
## Age 0.22656 0.00607 37.321 < 2e-16 ***
## resHeight 0.10909 0.00472 23.115 < 2e-16 ***
## SmokerNon 0.11023 0.06002 1.837 0.06672 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4189 on 650 degrees of freedom
## Multiple R-squared: 0.7676, Adjusted R-squared: 0.7665
## F-statistic: 715.7 on 3 and 650 DF, p-value: < 2.2e-16Отличия мы находим в таблице с предикторами. Здесь мы видим, что у Age и у resHeight коэффициенты остались как и прежде, но добавилась ещё одна строка — SmokerNon. Так как наша переменная содержит только два уровня, baseline какой-то из двух групп уходит в intercept — в данном случае это SmokerCurrent. Коэффициент при SmokerNon показывается, на сколько отличается baseline группы SmokerNon по сравнению со SmokerCurrent. Итак, объем форсированного выхода на первую секунду у некурящих детей на 0.11 литра больше, чем у курящих. Результат, вполне согласующийся со здравым смыслом.
Оценка и диагностика модели производится аналогично тому, как мы это делали на предыдущих моделях.
18.3 Модели со взаимодействием предикторов
Но можно ведь не только уловить различия в базовом уровне количественны предикторов в раз личных группах наблюдений, но и разную степень их связи с целевой переменной в этих группах. Для этоо нужно ввести взаимодействие предикторов в модель.
18.3.1 Математическая модель
В данном случае модель будет выглядеть так:
\[ y_i = b_0 + b_1 I_1 + b_2 x_2 + b_3 I_1 x_2 \]
Для простоты здесь один количественный и один категориальный предиктор. Переменная \(I_1\) снова выступает здесь индикатором. То есть наша модель как бы снова содержит в себе две «подмодели»:
- для наблюдений категории 1 (\(I_1 = 0\)) модель принимает следующий вид: \(y_i = b_0 + b_2 x_2\),
- а для наблюдений категории 2 (\(I_1 = 1\)) вот такой: \(y_i = (b_0 + b_1) + (b_2 + b_3) x_2\).
Теперь у нас не только есть поправочный коэффициент на baseline, но и поправочный угловой коэффициент для количественного предиктора.
18.3.2 Подбор модели
Взаиможействие предикторов можно указать двумя способами:
model4 <- lm(FEV ~ Age + Smoker + Age:Smoker, ofv) # : указывает на дополнительный угловой коэффициент для категории Smoker
model4 <- lm(FEV ~ Age * Smoker, ofv) # эквивалентна предыдущей записи, но корочеОбе команды построят идентичные модели. Взглянем на summary():
##
## Call:
## lm(formula = FEV ~ Age * Smoker, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.76645 -0.34947 -0.03364 0.33679 2.05990
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.19697 0.40596 5.412 8.78e-08 ***
## Age 0.07986 0.02959 2.699 0.00713 **
## SmokerNon -1.94357 0.41428 -4.691 3.31e-06 ***
## Age:SmokerNon 0.16270 0.03074 5.293 1.65e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5537 on 650 degrees of freedom
## Multiple R-squared: 0.5941, Adjusted R-squared: 0.5922
## F-statistic: 317.1 on 3 and 650 DF, p-value: < 2.2e-16Intercept содержит baseline для уровня Current переменой Smoker. Коэффициент при SmokerNon, как и в предыдущей модели, показывает, насколько отличается baseline для уровня Non переменной Smoker от базового уровня категории Current этой же переменной. Коэффициент при Age — это угловой коэффициент регрессионной прямой для категории SmokerCurrent, в то время как запись Age:SmokerNon показывается, то это добавочный угловой коэффициент для группы некурящих респондентов. Как видите, всё аналогично тому, как это задаётся в математической модели, поэтому если вы помните её, интерпретация результатов анализа не составляет особого труда.
18.4 Сравнение моделей
Часто нам надо сравнить две модели друг с другом. Зачем? Например, чтобы понять, можно ли данную модель упростить, ведь мы хотим найти наиболее простую и интерпретируемую модель, не так ли?
Как уже упоминалось выше, можно это сделать по значению скорректированного коэффициента детерминации, но можно использовать и другие показатели. Есть способ сравнить информативность двух моделей статистическим тестом — частным F-критерием. Делается это с помощью функции anova(), в которую необходимо передать сравниваемые модели.
Допустим мы хотим сравнить model2 и model3 — первая содержит два количественных предиктора, а вторая ещё и категориальный.
## Analysis of Variance Table
##
## Model 1: FEV ~ Age + resHeight
## Model 2: FEV ~ Age + resHeight + Smoker
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 651 114.67
## 2 650 114.08 1 0.59206 3.3733 0.06672 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Здесь мы смотрим на значение F-статистики и p-value — впрочем, как и обычно при тестировании статистических гипотез. Если модели статистически значимо различаются, то влияние предиктора, который присутствует в одной модели, но отсутствует в другой, статистически значимо. В данном случае мы видим, что обе модели в общем-то одинаковы по своей информативности — то есть введение предиктора Smoker не особо-то и улучшает модель, даже несмотря на то, что он статистически значим. Но мы получили значение p-value, которое говорит о том, что модели различаются на уровне статистической тенденции. Возможно, стоит обратить на это внимание.
Частный F-критерий можно рассчитать и с помощью другой функции — drop1(). Допустим, мы решили регрессировать нашу целевую переменную по всем переменным датасета сразу да ещё и со всеми взаиможействиями:
##
## Call:
## lm(formula = FEV ~ Age * Height * Sex * Smoker, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.42585 -0.22543 0.00276 0.22556 1.62815
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 25.71051 13.30602 1.932 0.0538 .
## Age -1.95406 1.00231 -1.950 0.0517 .
## Height -0.34974 0.20513 -1.705 0.0887 .
## SexMale -31.17265 15.46414 -2.016 0.0442 *
## SmokerNon -28.32508 13.33280 -2.124 0.0340 *
## Age:Height 0.03009 0.01547 1.946 0.0521 .
## Age:SexMale 1.60183 1.21164 1.322 0.1866
## Height:SexMale 0.47343 0.23620 2.004 0.0455 *
## Age:SmokerNon 1.92939 1.00829 1.914 0.0561 .
## Height:SmokerNon 0.42323 0.20565 2.058 0.0400 *
## SexMale:SmokerNon 34.15472 15.50337 2.203 0.0279 *
## Age:Height:SexMale -0.02410 0.01844 -1.307 0.1916
## Age:Height:SmokerNon -0.02860 0.01556 -1.838 0.0666 .
## Age:SexMale:SmokerNon -2.07178 1.21924 -1.699 0.0898 .
## Height:SexMale:SmokerNon -0.52090 0.23696 -2.198 0.0283 *
## Age:Height:SexMale:SmokerNon 0.03172 0.01856 1.709 0.0880 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3827 on 638 degrees of freedom
## Multiple R-squared: 0.8096, Adjusted R-squared: 0.8051
## F-statistic: 180.9 on 15 and 638 DF, p-value: < 2.2e-16В итоге мы получили, конечно, что-то значимое, но совершенно не интерпретабельное. Надо пытаться упрощать.
## Single term deletions
##
## Model:
## FEV ~ Age * Height * Sex * Smoker
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 93.465 -1240.4
## Age:Height:Sex:Smoker 1 0.42783 93.893 -1239.4 2.9204 0.08795 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Функция drop1() исключается по одному предиктору из модели, начиная со взаиможействий самого высокого порядка и сразу тестирует гипотезу о различии моделей. Необходимо в её аргументах указать test = "F", так как сейчас нас интересует именно F-критерий. Эта функция умеет считать ещё и другие — с ними мы столкнемся в следующих главах.
В данном случае мы видим, что при исключении из модели взаимодействия третьего уровня (то есть взаиможействия четырёх предикторов) информативность модели не изменится — а значит модель можно упростить.
Ещё одна полезная функция — это update(), чтобы не переписывать модель заново, а просто указать, какую её составляющую надо удалить:
Синтаксис . ~ . -x говорит о том, что «оставь формулу модели той же, но удали из неё предиктор x».
Снова протестиируем модель с помощью частного F-критерия:
## Single term deletions
##
## Model:
## FEV ~ Age + Height + Sex + Smoker + Age:Height + Age:Sex + Height:Sex +
## Age:Smoker + Height:Smoker + Sex:Smoker + Age:Height:Sex +
## Age:Height:Smoker + Age:Sex:Smoker + Height:Sex:Smoker
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 93.893 -1239.4
## Age:Height:Sex 1 1.67744 95.570 -1229.8 11.4160 0.0007724 ***
## Age:Height:Smoker 1 0.08082 93.974 -1240.8 0.5500 0.4585756
## Age:Sex:Smoker 1 0.00474 93.898 -1241.3 0.0322 0.8575529
## Height:Sex:Smoker 1 1.20821 95.101 -1233.0 8.2226 0.0042735 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Видим, что при удалении взаиможействий Age:Height:Smoker и Age:Sex:Smoker информативность модели не изменится — поочередно удалим. Почему лучше делать это поочередно? Так как при удалении предиктора из модели статистики других предикторов могут измениться:
## Single term deletions
##
## Model:
## FEV ~ Age + Height + Sex + Smoker + Age:Height + Age:Sex + Height:Sex +
## Age:Smoker + Height:Smoker + Sex:Smoker + Age:Height:Sex +
## Age:Height:Smoker + Height:Sex:Smoker
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 93.898 -1241.3
## Age:Height:Sex 1 1.6786 95.576 -1231.8 11.4412 0.0007621 ***
## Age:Height:Smoker 1 0.0811 93.979 -1242.8 0.5528 0.4574650
## Height:Sex:Smoker 1 1.2755 95.173 -1234.5 8.6939 0.0033091 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Single term deletions
##
## Model:
## FEV ~ Age + Height + Sex + Smoker + Age:Height + Age:Sex + Height:Sex +
## Age:Smoker + Height:Smoker + Sex:Smoker + Age:Height:Sex +
## Height:Sex:Smoker
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 93.979 -1242.8
## Age:Smoker 1 1.4059 95.385 -1235.1 9.5893 0.0020425 **
## Age:Height:Sex 1 1.7363 95.715 -1232.8 11.8424 0.0006166 ***
## Height:Sex:Smoker 1 1.1946 95.173 -1236.5 8.1478 0.0044507 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1И вот мы добрались до того момента, когда исключение любого из взаиможействий значимо ухудшит модель. То есть мы максимально упростили модель, насколько это возможно. Итоговая модель выглядит так:
##
## Call:
## lm(formula = FEV ~ Age + Height + Sex + Smoker + Age:Height +
## Age:Sex + Height:Sex + Age:Smoker + Height:Smoker + Sex:Smoker +
## Age:Height:Sex + Height:Sex:Smoker, data = ofv)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.42575 -0.22638 0.00352 0.22770 1.62661
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.559311 2.313757 0.674 0.500598
## Age -0.119427 0.113202 -1.055 0.291827
## Height 0.022225 0.035423 0.627 0.530599
## SexMale -4.668960 2.978608 -1.567 0.117492
## SmokerNon -4.042750 1.980650 -2.041 0.041648 *
## Age:Height 0.001818 0.001738 1.046 0.295947
## Age:SexMale -0.446116 0.134768 -3.310 0.000984 ***
## Height:SexMale 0.067449 0.045821 1.472 0.141504
## Age:SmokerNon 0.073548 0.023751 3.097 0.002043 **
## Height:SmokerNon 0.049233 0.030222 1.629 0.103798
## SexMale:SmokerNon 7.515828 2.604824 2.885 0.004041 **
## Age:Height:SexMale 0.007257 0.002109 3.441 0.000617 ***
## Height:SexMale:SmokerNon -0.112966 0.039576 -2.854 0.004451 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3829 on 641 degrees of freedom
## Multiple R-squared: 0.8086, Adjusted R-squared: 0.805
## F-statistic: 225.6 on 12 and 641 DF, p-value: < 2.2e-16Почему в неё остались незначимые предикторы? Так как оказались значимы взаимодействия, а включить в модель взаиможействия без самого предиктора невозможно.
Конечно, можно делать это не руками, а автоматически, но это уже относится к сфере машинного обучения. При этом не проводится содержательным анализ того, что происходит — пока же вы руками исключаете предикторы друг за другом, можно успеть подумать, что складывается в модели с содержательной точки зрения и почему.
Будем говорить о влиянии, помня о тех оговорках, которые мы обозначили в предыдущей главе — регрессия per se не показывает причинно-следственной связи.↩︎